角速度求积分能得到欧拉角吗_看懂蒙特卡洛积分(二) 蒙特卡洛估计与重要性采样...

TC130：看懂蒙特卡洛积分(一) 概率分布变换与随机采样​zhuanlan.zhihu.com

TC130：游戏渲染进阶​zhuanlan.zhihu.com

概率论背景

(1) 数学期望

设

是随机变量,

是

的函数,

.

A. 如果

是离散型随机变量, 其分布列为

.

随机变量

的

数学期望定义为

.

的数学期望定义为

.

B. 如果

是连续性随机变量, 其概率密度为

.

随机变量

的

数学期望定义为

.

的数学期望定义为

.

(2) 方差标准差

设

是随机变量,

的方差

定义为

.

称为

的标准差.

黎曼和

在开始讲蒙特卡洛估计之前, 我们先来回顾下黎曼和, 这样可以和下面对比, 加深印象.

设我们现在想求解积分

, 我们将

划分成N等份, 这样每一份的长度为

. 在每一小份中我们可以任取一个位置的值代表这一小份上

的平均值, 我们这里取每小份上左边的值(也可以取右边或者中间), 这样这个积分的

黎曼和为

当

, 黎曼和就趋近于定积分的值, 这也是定积分的一种定义方法.

黎曼和是一种简单有效的估计积分值的方法.

蒙特卡洛估计

蒙特卡洛估计(Monte Carlo Estimator)的原理很简单, 假设现在我们要求解一个一维的积分

. 已知一个概率密度为

的随机变量

, 蒙特卡洛估计可以表示为:

概率密度

需要满足

现在来验证下, 这种方式是正确的:

这种积分同样可以任意扩展到多维度的情况.

蒙特卡洛估计的采样次数

是可以任意确定的, 这是蒙特卡洛估计相对其他估计方式的一个重要的优点.

计算结果表明, 蒙特卡洛估计误差收敛的速度为

(意味着4倍的采样会使误差减少一半). 虽然在一维情况下不如其他的近似方法, 但由于蒙特卡洛估计不受维度影响, 在高维情况下比其他估计方法收敛要快得多.

重要性采样

现在我们有了蒙特卡洛估计方法, 下一步就是确定随机变量

的概率密度函数

.

一种简单的方式是直接直接使

在

上均匀分布,

为某个常数.

更好的方法使用重要性采样(importance sampling), 即使概率密度

和需要积分的函数

尽量接近.

重要性采样本身很好理解, 就是得到值更大的部分, 对结果影响也更大, 自然需要更多的采样. 这样我们把有限的采样次数合理地分配在每个区间上.

值得注意的是, 一个不好的概率密度函数反而会使得结果的误差增大.

有的时候, 需要积分的方程中可能包含多个需要积分的部分, 这时候就需要用到多重重要性采样(multiple importance sampling/MIS).

比如现在要求解

这样的积分时, 两个部分分别对应两个概率密度

, MIS给出的新的蒙特卡洛估计为:

分别是两边的采样次数,

分别是两个部分对应的权重.

一个常用的权重函数为:

在上面有两个部分的情况下得:

分层采样

有了上面得部分, 我们已经得到得完整的蒙特卡洛估计的步骤, 可以开始进行求解问题了.

比如现在要采样10次, 就取

, 然后随机10次, 计算累加结果就可以了.

这时我们又遇到了一个问题, 那就是这样独立地随机, 产生的随机结果是不均匀的, 会使结果的误差增大.

一个好的随机过程是取一系列的采样序列, 采样序列是一个复杂深奥的话题, 我们这里仅仅介绍下最简单的分层采样(Stratified Sampling). 我计划在其他的文章中讲这个话题, 读者也可以参考这个文刀秋二：低差异序列（一）- 常见序列的定义及性质.

分层采样的原理就是采样的样本空间均匀分成n等份, 在每份中取一个采样点. 为了减少采样结果的走样, 在每份中采样时加上一点抖动. 下图是一个简单的示例, 可以看出, 分层采样的结果更加均匀.

(a) 纯随机采样; (b) 直接分层采样; (c) 带抖动的分层采样

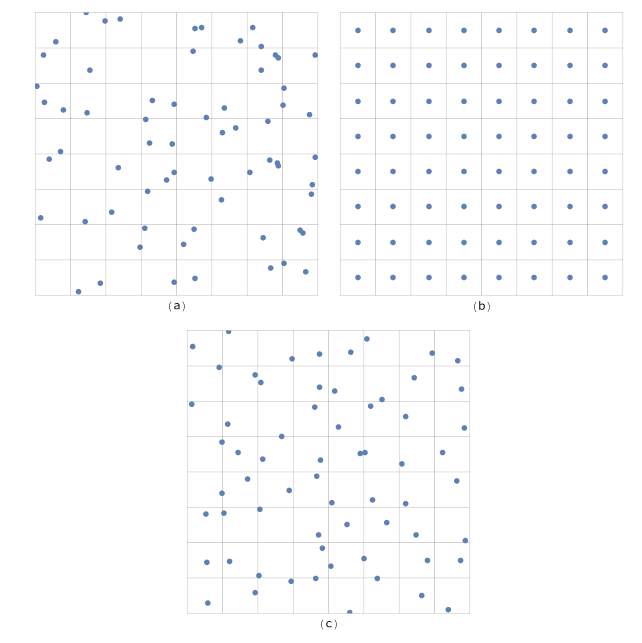
实践:IBL漫反射贴图

游戏中常用一个cubemap来表示环境光照, 在求解物体表面的环境光漫反射时, 通常会将漫反射贴图预积分计算出来.

漫反射的方程为:

左边的部分是不会变化的, 提出来得到:

这样我们就可以把

部分提前计算出来, 在实时渲染中就不需要再求积分. 这个过程也叫做求irradiance map.

现在我们尝试用两种方式来求解:

A. 黎曼和

将

分别划分成

份, 得:

其实这里也可以看成是蒙特卡洛估计:

B. 蒙特卡洛估计

我们这里按照余弦权重来采样, 使用分层采样分别将

取

次, 得到随机在单位圆上的点

由Malley方法映射到单位半球面上, 得到

已知

, 蒙特卡洛估计为:

我写了一份对全景图求irradiance map的python实现的代码, 放在这里raphael10241024/monte_carlo_demo, 从结果上来看, 相同采样次数下, 蒙特卡洛估计要优于黎曼和估计.

蒙特卡洛积分的高级应用有很多, 但是基本原理都是基于这两篇文章所讲的内容. 这个系列先写到这里, 后面看情况再补充新的.