傅里叶变换尺度变换性质_积分变换（2）——傅里叶变换

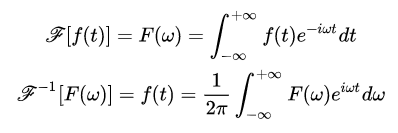
学习阶段：大学数学，积分变换。

前置知识：微积分、复变函数、傅里叶级数。

tetradecane：积分变换（1）——傅里叶级数​zhuanlan.zhihu.com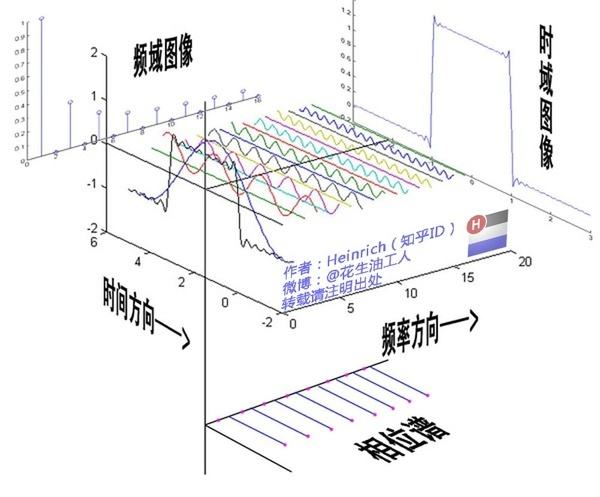

傅里叶级数有其局限性。考虑将

区间上的函数

转化为傅里叶级数

，容易发现而该级数以

为周期，于是会出现图1的情况：

图1 傅里叶级数是周期函数

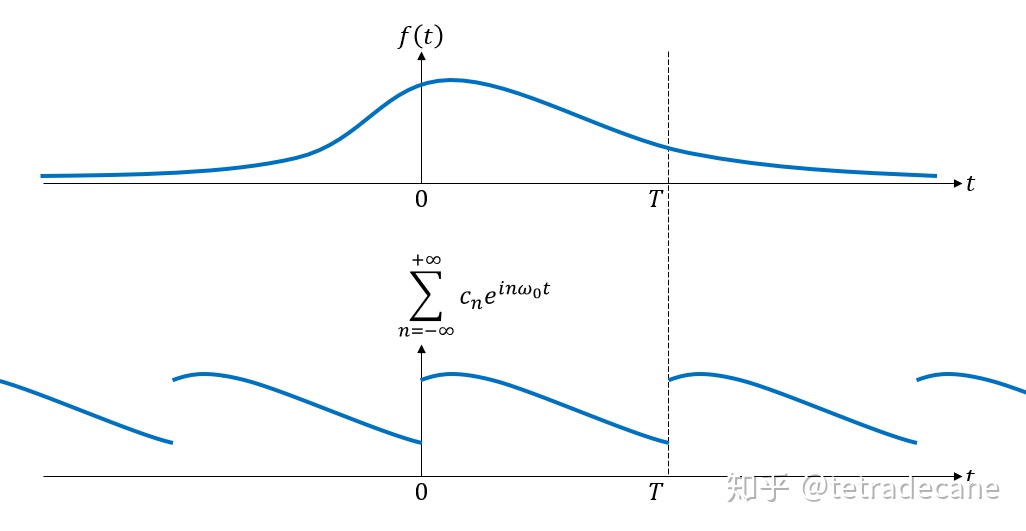
因此，对于非周期函数，没有傅里叶级数能在

的区间上收敛到它。但是，我们可以认为非周期函数是周期无穷大的函数，试着将傅里叶级数中的

推广到无穷大。

1. 傅里叶变换

1.1 推广傅里叶级数到无穷区间

我们首先对函数

在区间

上展开为傅里叶级数得

考虑让

，这样就把

上的函数

全部纳入了考虑范围。此时

，

可视为相邻频率的周期函数的频率间隔

，那么

可视为连续变化的，记

. 那么

如果

收敛，则

是个无穷小量。这是可以理解的，因为

描述的是在区间

上

路径的重心，只有分量

会造成影响。当

时，造成影响的分量也被稀释掉了。可以想象一卷线圈，匝数非常多，即便线圈的头和尾没有对齐，其重心也基本是在几何中心。

将上式

代回到傅里叶级数中，得到

取

极限得到

上式被称为傅里叶积分定理。

1.2 傅里叶变换

我们记

在确定

后，该函数只与给定的频率

有关，它描述的是

中分量

的分布密度。称该函数为

的

频谱密度函数（简称为连续频谱或频谱）。

从理解上来说，视

频率区间中的分量

频率恒定，它的系数近似为

. 如图2所示：

图2 频谱密度的含义

对任何一个函数

都可以尝试通过这种操作变为另一个对应的函数

，因此这是一个函数的函数，称之为（连续时间）

傅里叶变换（Fourier Transform, FT）或傅氏变换，记为

在函数变换中，称

是

的

象函数，称

是

的

象原函数。与傅里叶级数类似，称

为

的

振幅谱，

为

的

相位谱。

得到频谱函数后，自然可以把它逆变换回去，即

称该变换为傅里叶逆变换，记为

2. 广义傅里叶变换

2.1 狭义傅里叶变换的局限性

如果

是周期函数，它能完整地用傅里叶级数表示，但它反而求不出傅里叶变换。因为它的分量是离散分布的，求不出分布密度。

例如周期函数

，它的离散频谱为

. 我们试着求它的傅里叶变换：

这里产生了两个问题：

①在

时，广义积分

震荡不收敛。

这个问题比较好解决。规定它的值为

，即可与傅里叶级数相容。

②在

时，广义积分

发散到正无穷大。

如果我们仅仅是简单地在

上挖去这些无穷大的点，那么我们会无法区分

中，分量

和

的系数。如果没有这些系数，我们将无法进行逆变换，无法通过

还原出

的原貌。

2.2 单位冲激函数

为了解决上述问题，我们引入了单位冲激函数，又称狄拉克

函数

。这是一个广义函数，并不能由通常的数集映射来定义，必须依赖于积分。广义函数在泛函分析中有详细讨论，这里只简单介绍一下它的直观定义：

①对于任意

满足

；

②满足积分

.

显然，

函数并不能简单地记为

，因为这并不能体现性质②，也就无法体现

与

的区别。

函数有许多直观的近似方法，以下举两例：

，这是矩形冲激函数（图4红线）的极限状态。

，这是

导函数（图4蓝线）的极限状态。

图4 δ函数的近似

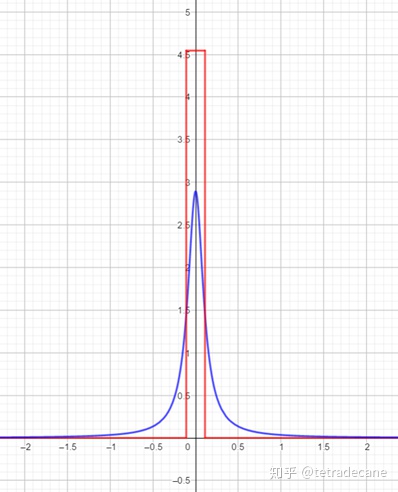
容易证明他们满足性质②，且在极限状态下满足性质①。

通常，在画函数图像时，冲激函数用一箭头表示，并标上它的冲激强度。

在

的冲激强度就是

. 图5是一些例子：

图5 冲激函数的图示

函数并不是真实存在的函数，它最初是用来描述物理中的理想模型的，例如质点、点电荷这种没有尺度的模型。关于它们的很多函数只会在图像上有一瞬间的脉冲，用

函数就能很好地描述。

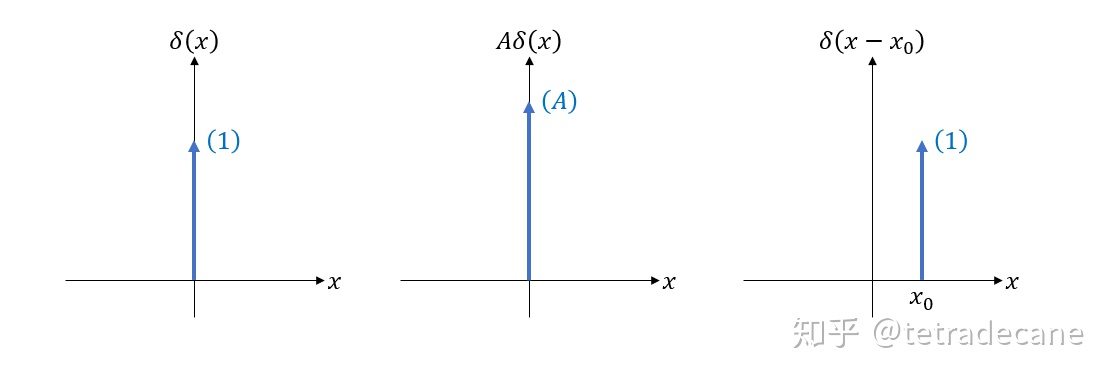
以下给出

函数的一些性质：

①筛选性质：

；

②是偶函数，即

；

③放缩/相似性：

；

④是单位阶跃函数

的导函数。

2.3 广义傅里叶变换

利用

函数，我们就可以把傅里叶级数中的离散频谱数列也表示成傅里叶变换得到的连续频谱函数。涉及到

函数的傅里叶变换，被称为

广义傅里叶变换，它能对周期函数进行傅里叶变换。

首先，我们对

函数进行傅氏变换，得到

也就是说，

均匀地含有各种频率分量且系数相等，称此为

均匀频谱或白色频谱。直观上可以这样理解：只有在

时各个分量

齐心协力都为1，叠加得到无穷大；而在

时各个分量杂乱无章，平均而言就得0.

那么常数1的傅里叶逆变换应得到

，即

得到了一个十分重要的公式：

. 换元即可得到

，也就是说常数1的连续频谱为

.

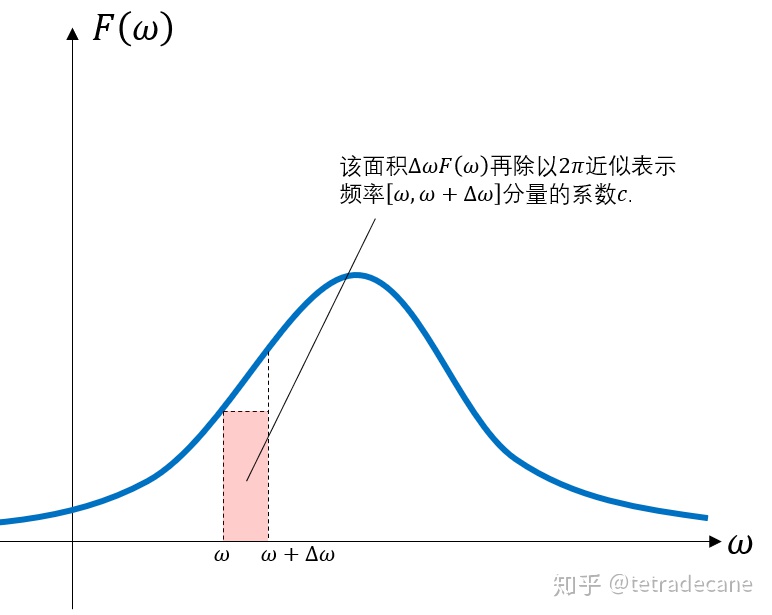
上述公式也可以通过离散情况的极限来直观得出。如图6所示，积分

的值仅在

处为

，其他情况均为

. 而频率间隔

，因此它构成一个矩形冲激函数，矩形的面积为

. 在

时，自然得到了冲激强度为

的函数

.

图6 δ函数的重要公式的直观解释

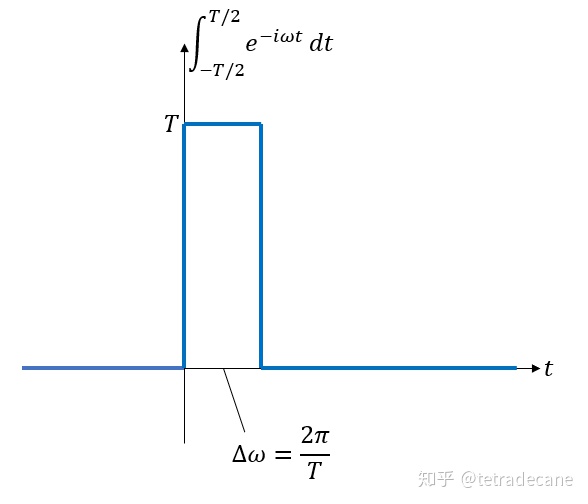
由此，在2.1节提到的函数

就可轻易求出其傅里叶变换为

而且它还能逆变换回去：

对

的连续频谱作图得图7：

图7 e^(it)+2e^(2it)的连续频谱

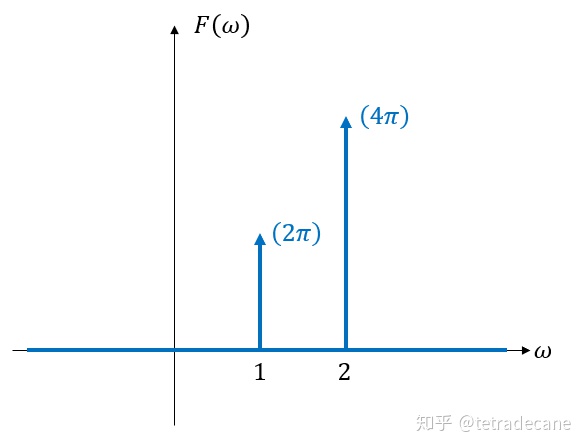
立刻可以读出其傅里叶级数的系数分别为1和2. 因此，连续频谱能表示离散频谱，离散频谱能转换为连续频谱，它们是一一对应的。

附录

推荐视频：

【官方双语】形象展示傅里叶变换​www.bilibili.com