蒙特卡洛采样_随机模拟：马尔可夫链中的蒙特卡洛推断采样法MCMC「1」

最近学习了机器学习中的马尔科夫链蒙特卡洛(Markov Chain Monte Carlo, 简称MCMC) 相关的知识。

主要内容包括：

【1】蒙特卡洛原则，及其应用于采样的必要性

【2】用于求解最大似然、近似推断、期望问题的经典采样算法：Metropolis-Hastings，Rejection，Importan，Metropolis和Gibbs算法。

【3】马尔可夫链各个性质在蒙特卡洛采样问题中的应用，包括同质性，平移不变性

————————————————【1】——————————————————

MC采样的基本想法是，选择一个样本，用一个简单问题近似复杂的混合问题。对于一个复杂分布，使用从中获得的样本来表示该分布，而不是直接猜测该分布。

首先学习复杂分布与近似推断approximate inference的例子：

【需要采样的第一类场景】贝叶斯推断与学习：假设未知变量x，已知数据y，下列难以处理的整合问题是贝叶斯统计的中心问题。

1、正态化问题

已知p(x)先验，似然p(y|x)，为求得后验概率p(x|y)，需要计算贝叶斯理论中的正态系数：

而这个分母，若x维度很大，是不能直接计算的

这个分母也就是对似然和先验关于x求边缘分布，得到p(y)。由于分母不能直接计算，转而从P(x|y)后验分布中采样，之后用采样的样本们表示此分布。更多的样本来自后验概率大的情况。近似推断在这里就是用样本的集合近似后验概率分布，而不是使用上图中公式直接计算之。

2、边缘分布问题

给定一个具有隐变量z的联合分布(x,z)-y，求边缘后验(边缘概率分布)P(x|y)，需对隐变量z积分。若z维度过高，则难以处理。从该分布中采样而非求积分。

3、求期望

假定目的为获取如下格式的描述统计结果：

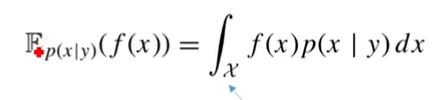
在给定观测值y的x的条件概率分布上，对函数fx求期望

求该条件概率的期望需要对x作条件积分，当x高维时难以处理。上式的含义为，给定y，特化了x的集合，只对这种情况下的x求期望。

【需要采样的第二类场景】优化，通常直接计算所有方案取最优是不可计算的。

【蒙特卡洛原则】从定义在一个很高维度空间的变量X的目标概率密度函数p(x)中，独立同分布地抽取样本xi N次。这N个样本被用来近似目标概率密度函数，使用如下的经验点质量函数(empirical point-mass function)：

经验点质量函数

经验点质量函数-计算x取某个特定值的概率。

【大数弱定律】当n趋近正无穷时，样本均至值按照概率收敛期望(真实分布均值)。但仍存在一个间隔。

【大数强定律】当n趋近正无穷时，样本均至值几乎完全收敛期望(真实分布均值)。

蒙特卡洛原则

P(x)可能是一个非常复杂的分布，从X中抽取N个样本xi，函数f的样本均值逼近函数f在x上的期望(应用强大数定律)。

若此f(x)的方差(population variance总体方差)不是无穷大，且等于Ep(x)[f(x)^2]-I(f)^2,则IN(f)样本均值f的方差为f(x)的方差/N。样本方差是总体方差的1/N。

【中心极限定理】样本估计f和真实f的差，在N趋向正无穷时趋向0。差*sqrt(N)服从N(0，总体方差)。

x_ =argmax P(xi) xi来自N个样本之一。

【非参数表示】

概率分布可以被参数表示为分布及其参数，也可以被从该分布中抽取的假设/样本集合表示。非参数表示的优点有不限制分布的类型。

至此，明白了MC原则和抽样的必要性，【2】将解决怎么从函数/分布里抽样的问题。