逻辑回归算法原理_【算法原理】逻辑回归

逻辑回归属于经典的二分类算法，但是为什么叫回归呢？
是因为逻辑回归可以通过sigmoid函数，将线性回归的结果（数值）映射为概率，有了概率，就可以根据概率大小判断属于哪一类。

Sigmoid函数公式及其几何表示

可以将线性回归方程作为z带入该公式，将值转换为概率，预测转换为分类

该函数的自变量取值范围是负无穷到正无穷，因变量取值范围是0到1，刚好与概率取值范围相同，适合0-1二分类问题

Sigmoid函数整合

现在将一个线性回归方程带入sigmoid函数：

由函数的几何表示可知：

Y属于1类的概率是h(x)的话，Y属于0类的概率就是1-h(x)

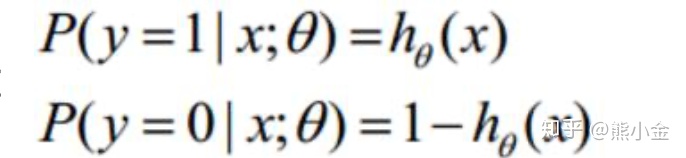
上述两个式子可以用一个函数整合表示：

1式

逻辑回归求解

求解过程与线性回归求解方法相同：

先构造极大似然函数：

取对数：

因为要求上式取得最大概率的最优参数塞塔，所以考虑使用梯度下降法，但是对于上式来说好像应该叫“梯度上升法”（上篇文章中为了使得损失函数结果最小，使用梯度下降法；但是现在我们想让概率最大，所以应该是梯度上升）？

为了使用梯度下降，需要对上式进行简单的变换：

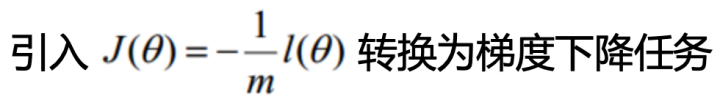
接下来就是梯度下降法的步骤：

J(塞塔)对塞塔求偏导，得到“下山一步”的变化值：

对参数塞塔进行更新：

对与机器学习算法的选择，能选择简单的就不选择复杂的。
逻辑回归作为简单的二分类算法，非常好用并且非常常用。

---

逻辑回归实现模版：

from sklearn.linear_model import LogisticRegression
LR = LogisticRegression()
# LogisticRegression()的参数：
# solver = 'liblinear'
# max_iter = 100 梯度下降法最大迭代次数
# penalty = 'l1'/'l2' l1/l2正则对抗过拟合，l1/l2正则是利用误差项提高模型泛化能力
# C = 0.5 正则的参数
lr = LR.fit(x_train, y_train)

个人学习，严禁转载