本文介绍了OpenGL中的向量和矩阵概念，包括单位向量、点乘、叉乘以及矩阵的基本操作。讲解了矩阵在OpenGL中的作用，如视图变换和模型变换，并提到了矩阵堆栈在图形变换中的应用。
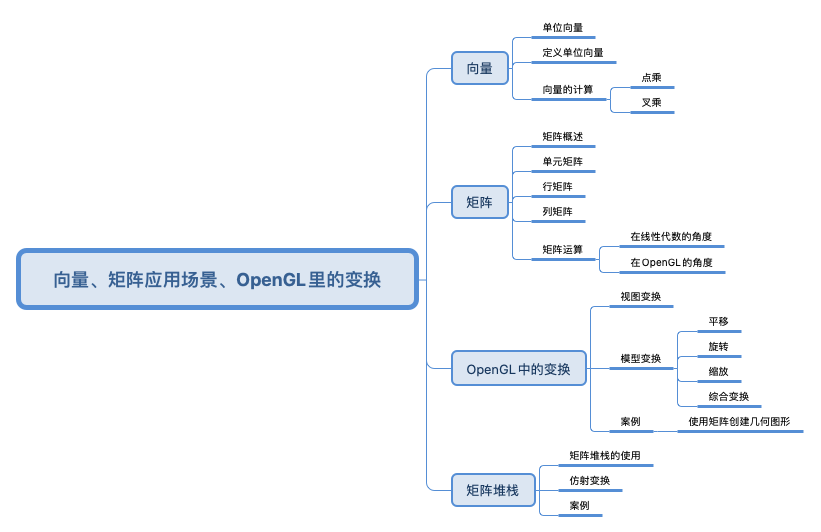
0.前言
在OpenGL中用到的数学叫3D数学，就是在上学的时候就是那门叫做线性代数的课程。但是对于线性代码不怎么好的同学来说，其实这个不用特别的关注这个。在对于学习OpenGL有⼀个误区，就是⼤家认为如果不能精通那些3D图形数学知识，会让我们⼨步难⾏，其实不然。就像我们不需要懂得任何关于汽⻋结构和内燃机⽅⾯的知识也能每天开⻋。但是，我们最好能对汽⻋有⾜够的了解，以便我们意识到什么时候需要更换机油、定期加油、汽⻋常规保养⼯作。同样要成为⼀名可靠和有能⼒的OpenGL程序员，⾄少需要理解这些基础知识，才知道能作什么？以及那些⼯具适合我们要做的⼯作。
初学者，经过⼀段时间的实践，就会渐渐理解矩阵和向量。并且培养出⼀种更为直观的能⼒，能够在实践中充分利⽤所学的内容。
即使⼤家现在还没有能⼒在脑海中默算出2个矩阵的乘法、也要明⽩矩阵是什么？以及这些矩阵对OpenGL意味着什么？
GLTools库中有⼀个组件叫Math3d,其中包含了⼤量好⽤的OpenGL ⼀致的3D数学和数据类型。虽然我们不必亲⾃进⾏所有的矩阵和向量的操作，但我然知道它们是什么？以及如何运⽤它们.在开发过程我们涉及到的图形变换,就会涉及到矩阵/向量的计算。例如⼤家在使⽤CAnimation 实现仿射变换,就使⽤了OpenGL渲染技术。
1.向量
1.1.单位向量
在3D笛卡尔坐标系，基本上⼀个顶点就是XYZ坐标空间上的⼀个位置。⽽在空间中给定的⼀个位置恰恰是由⼀个单独的XYZ定义的. ⽽这这样的 XYZ 就是向量。PS：在数学思维中，⼀个顶点也就是⼀个向量。
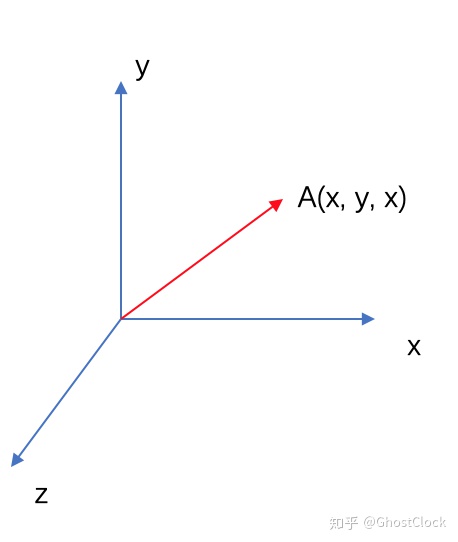
对于点A(x, y, z)可以得到在x方向的值，y方向上的值，z方向上的值在X轴方向上的值。
单位向量：长度为1的向量称之为单位向量。例如在X轴上的向量为(1, 0, 0)，又或者(0, 1, 0)的向量。
向量的长度(向量的模)：
计算公式：
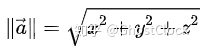
如果⼀个向量不是单位向量，⽽我们把它缩放到1， 这个过程叫做标准化。将⼀个向量进⾏标准化，就是将它的缩为1， 也叫做单位化向量。转为单位向量，最后得到了这个点在坐标系中的方向。
1.2.定义单位向量
math3d库，有2个数据类型，能够表示⼀个三维或者四维向量。
M3DVector3f：可以表示⼀个三维向量（x, y, z）。
M3DVector4f：可以表示⼀个四维向量（x, y, z, w)。 // W为缩放因子
在典型情况下，w坐标设为1.0。x, y, z值通过除以w来进⾏缩放。⽽除以1.0则本质上不改变x, y, z值。
//三维向量/四维向量的声明
typedef float M3DVector3f[3];
typedef float M3DVector4f[4];
//声明⼀个三维向量 M3DVector3f:类型 vVector:变量名
M3DVector3f vVector;
//声明⼀个四维向量并初始化⼀个四维向量
M3DVector4f vVertex = {0, 0, 1, 1};
//声明⼀个三分量顶点数组，例如⽣成⼀个三⻆形
//M3DVector3f vVerts[] = {
-0.5f,0.0f,0.0f,
0.5f,0.0f,0.0f,
0.0f,0.5f,0.0f
};M3DVector3f和M3DVector4f，其实就是一个普通的一维数组。
1.3.向量的计算
向量可以进⾏加法，减法计算。但是向量⾥有⼀个在开发中使⽤价值⾮常⾼的操作,叫做“点乘(dot product)”。点乘只能发⽣在2个向量之间进⾏。不能发生在向量和标量之间。(标量：其实就是一个数字，只有大小。例如：123，321等)。
1.3.1.点乘
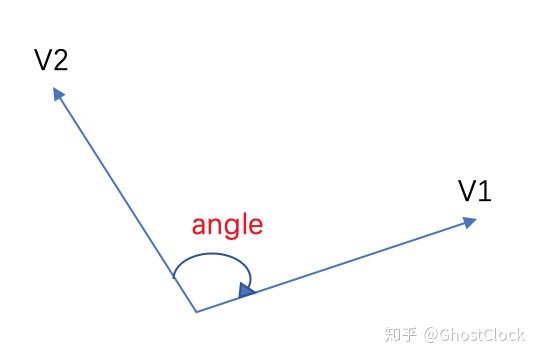
2个(三维向量)单元向量之间进⾏点乘运算将得到⼀个标量(不是三维向量, 是⼀个标量)。它表示两个向量之间的夹⻆。
得到两个向量之间的夹角：
前提条件: 2个向量必须为单位向量;
动作: 2个三维向量之间进⾏点乘；
结构: 返回⼀个[-1,1]范围的值. 这个值其实就是夹⻆的cos值(余弦值)。
单位化向量：(x / |xyz|, y / |xyz|, z / |xyz| )；即使⽤⼀个⾮零向量除以它的模(向量的⻓度)，就可以得到⽅向相同的单位向量。
math3d 库中提供了关于点乘的API：
//1.m3dDotProduct3 函数获得2个向量之间的点乘结果;
float m3dDotProduct3(const M3DVector3f u, const M3DVector3f v);
//2.m3dGetAngleBetweenVector3 即可获取2个向量之间夹⻆的弧度值;
float m3dGetAngleBetweenVector3(const M3DVector3f u, const M3DVector3f v);1.3.2.叉乘
向量之间的叉乘(cross product)，也是在业务开发⾥⾮常有⽤的⼀个计算⽅式。 2个向量之间叉乘就可以得到另外⼀个向量，新的向量会与原来2个向量定义的平⾯垂直。同时进⾏叉乘，不必为单位向量。(比如需要得到某一个面的法线，就可以使用向量的叉乘，且叉乘不满足交换律，否着的话得到的结果就会方向相反）。
前提: 2个普通向量
动作: 向量与向量叉乘
结果: 向量(垂直于原来2个向量定义的平⾯的向量).
math3d 库中提供了关于叉乘的API：
//m3dCrossProduct3 函数获得2个向量之间的叉乘结果得到⼀个新的向量
void m3dCrossProduct3(M3DVector3f result, const M3DVector3f u, constM3DVector3f v);2.矩阵(Matrix)
2.1.矩阵概述
假设在空间有⼀个点，使⽤xyz描述它的位置，此时让其围绕任意位置旋转⼀定⻆度后我们需要知道这个点的新的位置，此时需要通过矩阵进⾏计算;因为新的位置的x 不单纯与原来的x还和旋转的参数有关. 甚⾄于y和z坐标有关。
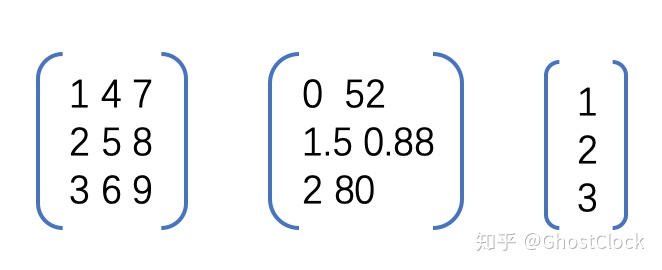
矩阵只有⼀⾏或者⼀列都是合理的。只有⼀⾏或者⼀列数字可以称为向量，也可以称为矩阵。
//三维矩阵/四维矩阵的声明
typedef float M3DMatrix33f[9];
typedef float M3DMatrix44f[16];在其他编程标准中，许多矩阵库定义⼀个矩阵时,使⽤⼆维数组；但是在OpenGL的约定⾥，更多倾向使⽤⼀维数组。这样做的原因是OpenGL使⽤的是 Column-Major(以列为主)矩阵排序的约定(在数学上叫转置矩阵)。
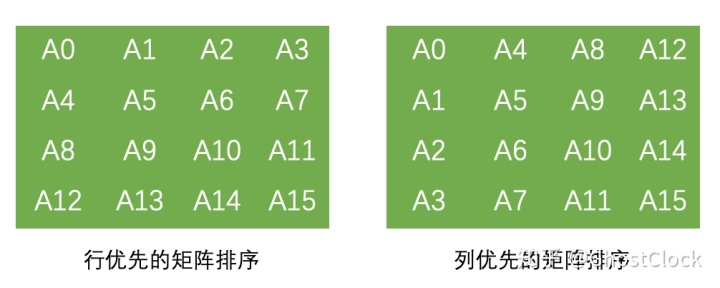
在OpenGL中，矩阵是列优先的。
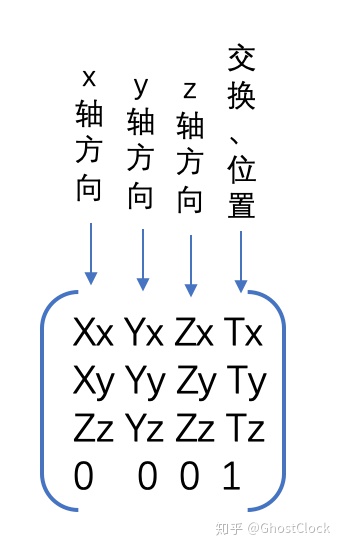
如上图所示，在OpenGL中列向量进⾏了特别的标注：矩阵的最后⼀⾏都为0，只有最后⼀个元素为1。如果将⼀个对象所有的顶点向量乘以这个矩阵，就能让整个对象变换到空间中给定的位置和⽅向。
2.2.单元矩阵
2.2.1.单元矩阵的定义
在OpenGL中定义单元矩阵:
方式一：
GLFloat m[] = {
1,0,0,0, //X Column
0,1,0,0, //Y Column
0,0,1,0, //Z Column
0,0,0,1 // Translation
}方式二：
M3DMatrix44f m = {
1,0,0,0, //X Column
0,1,0,0, //Y Column
0,0,1,0, //Z Column
0,0,0,1 // Translation
}方式三：
void m3dLoadIdentity44f(M3DMatrix44f m);2.2.2.矩阵相乘
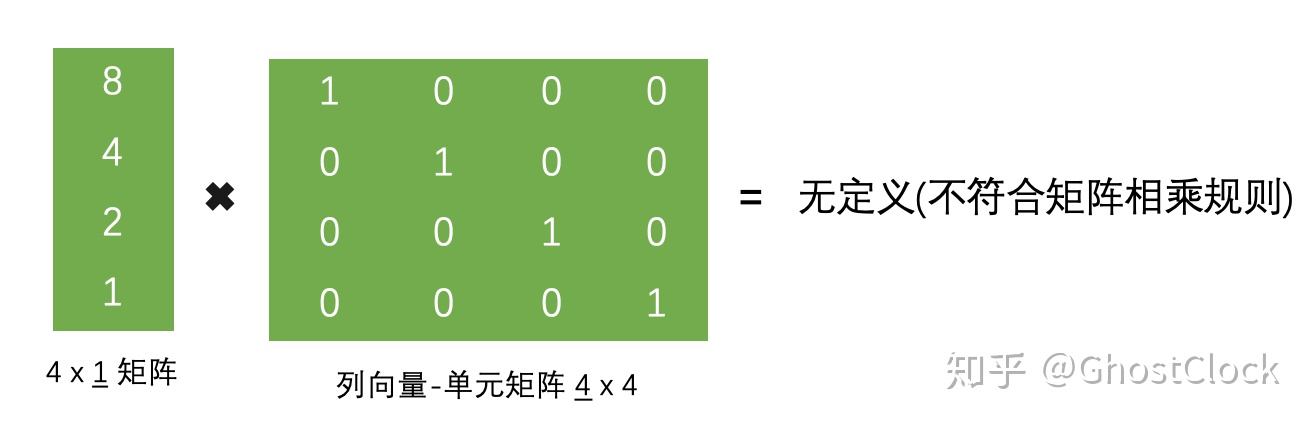
将⼀个向量 ✖ 单元矩阵 ,就相当于⼀个向量 ✖ 1，不会发⽣任何改变。
当两个矩阵相乘时，前面矩阵的行数必须和后面矩阵的列数相等才能相乘，且不满足交换律。
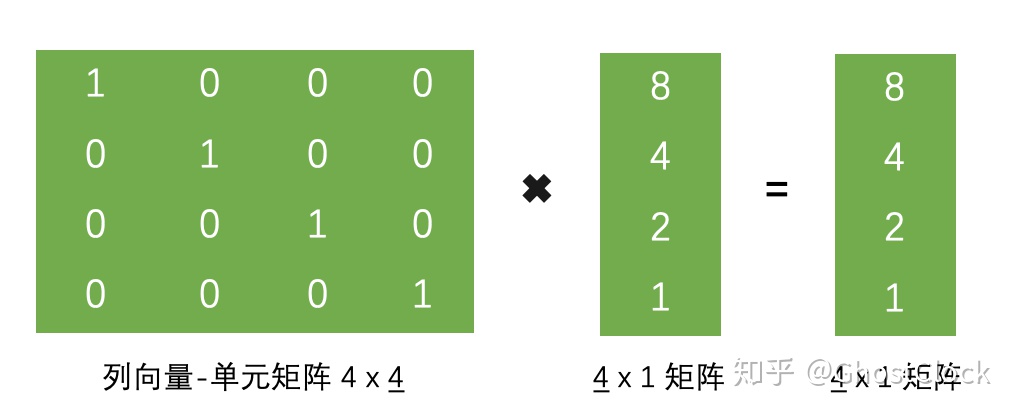
2.2.3.在线性代数的角度
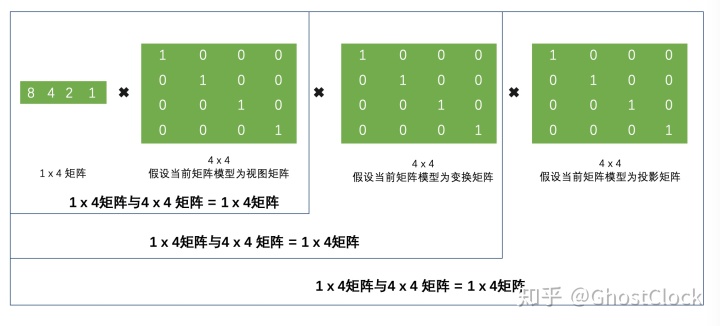
在线性代数数学的维度,为了便于书写，都是以行矩阵为标准来计算，都是从左往右顺序，进⾏计算。
如下列公式:
变换后顶点向量 = V_local * M_model * M_view * M_pro
变换后顶点向量 = 顶点 ✖ 模型矩阵 ✖ 观察矩阵(视图变换) ✖ 投影矩阵
2.2.4.在OpenGL角度
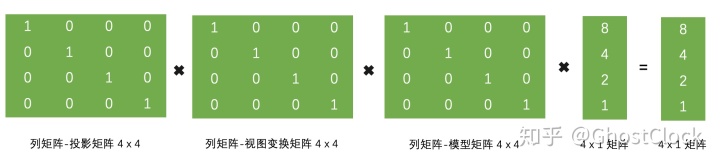
在OpenGL 的维度. 如下列公式:
变换顶点向量 = M_pro * M_view * M_model * V_local
变换顶点向量 = 投影矩阵 ✖ 视图变换矩阵 ✖ 模型矩阵 ✖ 顶点
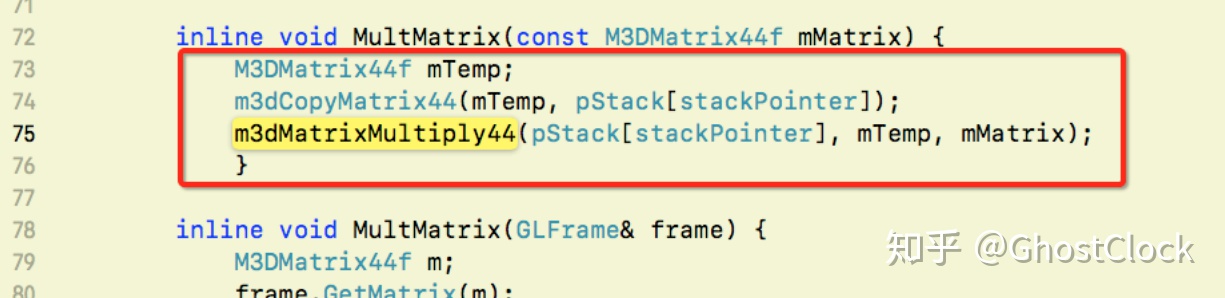
1. 从栈顶获取栈顶矩阵 复制到 mTemp
2. 将栈顶矩阵 mTemp 左乘 mMatrix
3. 将结果放回栈顶空间⾥;
在顶点着色器中使用矩阵相乘(glsl代码)：
3.OpenGL里的变换
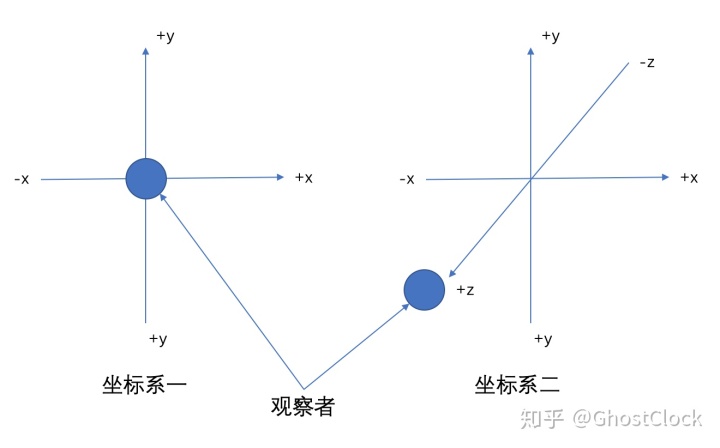
对于坐标系一，观察者垂直于屏幕，看上就就是一个点。对于坐标系二，观察者有所偏移，不垂直于屏幕。
3.1.视图变换
视图变换是应⽤到场景中的第⼀种变换，它⽤来确定场景中的有利位置,在默认情况下， 透视投影中位于原点(0, 0, 0)，并沿着 z 轴负⽅向进⾏观察 (向显示器内部”看过去”)。
当观察者点位于原点(0, 0, 0) 时，就像在透视投影中⼀样，视图变换将观察者放在你希望的任何位置，并允许在任何⽅向上观察场景，确定视图变换就像在场景中放置观察者并让它指向某⼀个⽅向；从⼤局上考虑，在应⽤任何其他模型变换之前，必须先应⽤视图变换。这样做是因为，对于视觉坐标系⽽⾔，视图变换移动了当前的⼯作的坐标系，后续的变化都会基于新调整的坐标系进⾏。
截⾃ <OpenGL 超级宝典 第5版 > 第96⻚
3.2.模型变换
模型变换: ⽤于操纵模型与其中某特定变换. 这些变换将对象移动到需要的位置. 通过旋转,缩放,平移等。
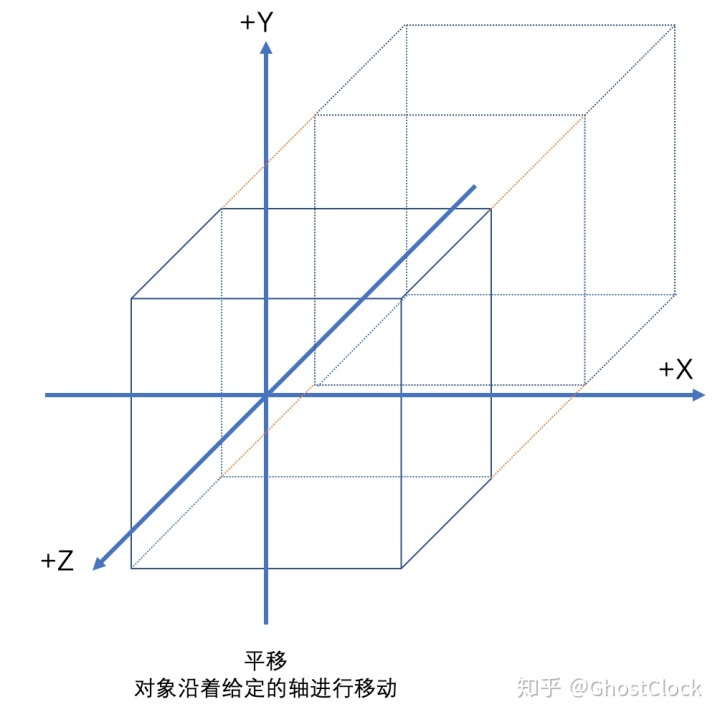
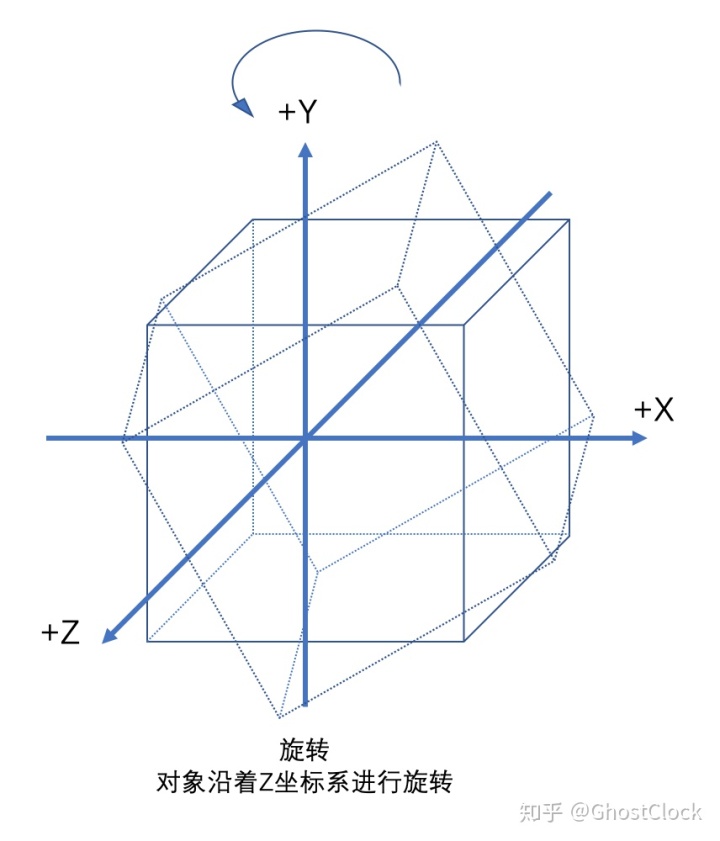
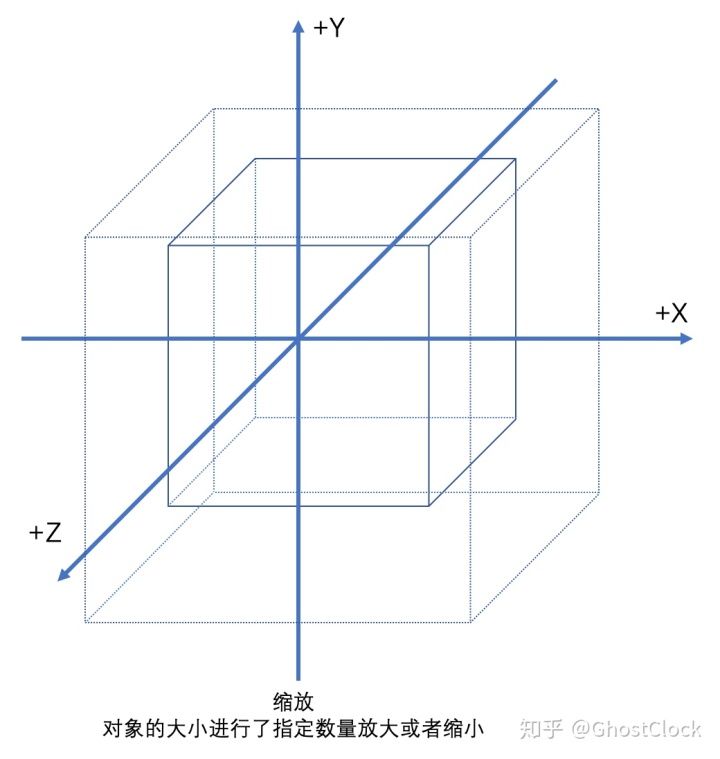
注意：如果执行变换的步骤不一样，那么得到的结果也可能不一样
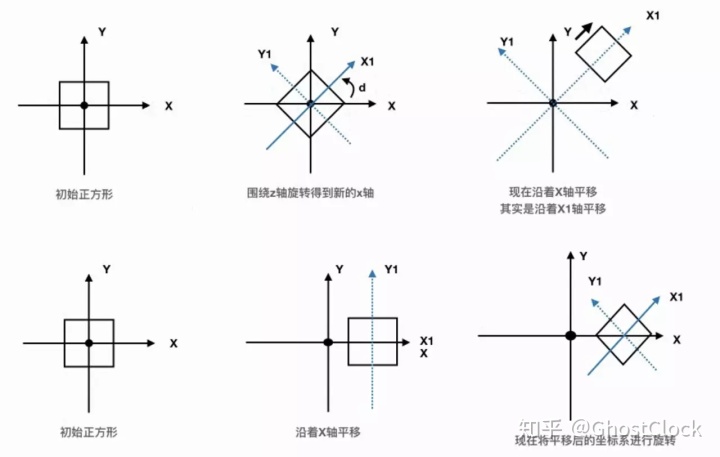
如上图所示：先旋转再平移和先平移再旋转得到结果不一样。
两种看待模型变换的方式：
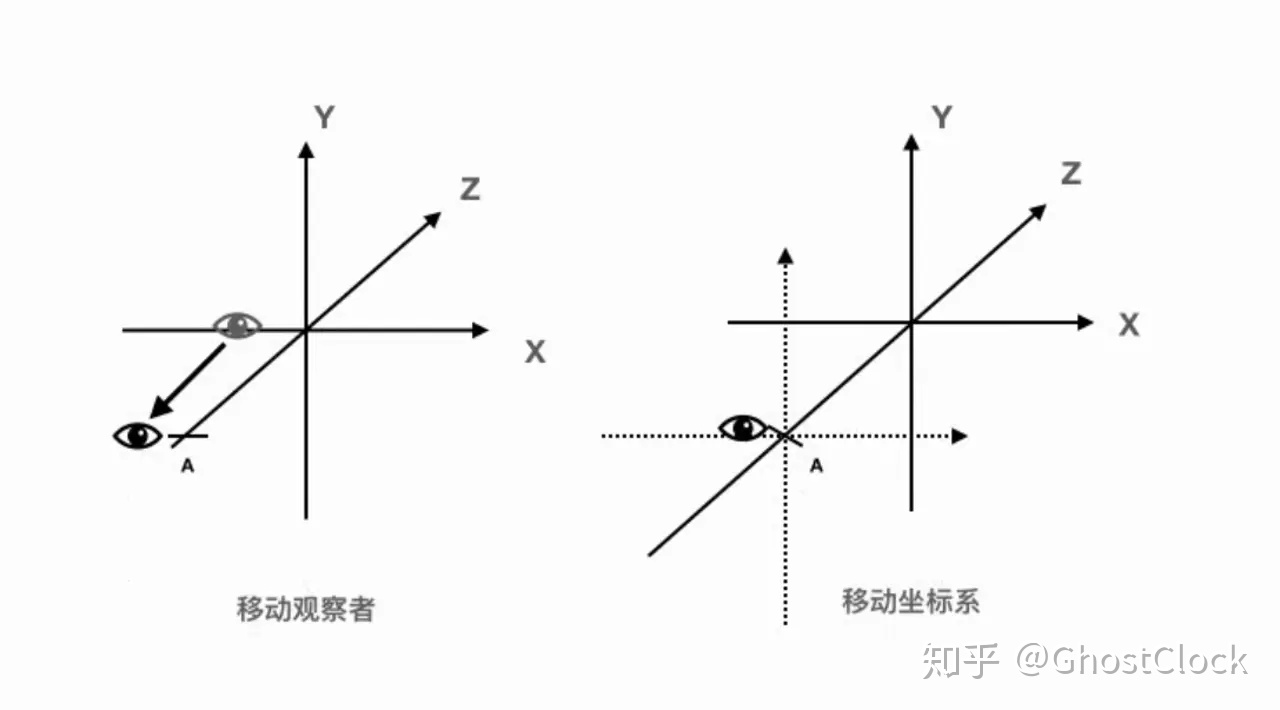
平移:
void m3dTranslationMatrix44(M3DMatrix44f m, floata x, float y, float z);旋转:
m3dRotationMatrix44(m3dDegToRad(45.0), floata x, float y, float z);缩放：
void m3dScaleMatrix44(M3DMatrix44f m, floata xScale, float yScale, float zScale);综合变换：
void m3dMatrixMultiply44(M3DMatrix44f product, const M3DMatrix44f a, const M3DMatrix44f b);案例：
添加案例6：使用矩阵创建几何图 形
4.矩阵堆栈
4.1.矩阵堆栈的使用
//类型
GLMatrixStack::GLMatrixStack(int iStackDepth = 64);
//在堆栈顶部载⼊⼀个单元矩阵
void GLMatrixStack::LoadIdentity(void);
//在堆栈顶部载⼊任何矩阵
//参数：4*4矩阵
void GLMatrixStack::LoadMatrix(const M3DMatrix44f m);
//矩阵乘以矩阵堆栈顶部矩阵，相乘结果存储到堆栈的顶部
void GLMatrixStack::MultMatrix(const M3DMatrix44f);
//获取矩阵堆栈顶部的值 GetMatrix 函数
//为了适应GLShaderMananger的使⽤，或者获取顶部矩阵的副本
const M3DMatrix44f & GLMatrixStack::GetMatrix(void);
void GLMatrixStack::GetMatrix(M3DMatrix44f mMatrix);
//将当前矩阵压⼊堆栈(栈顶矩阵copy ⼀份到栈顶)
void GLMatrixStack::PushMatrix(void);
//将M3DMatrix44f 矩阵对象压⼊当前矩阵堆栈
void PushMatrix(const M3DMatrix44f mMatrix);
//将GLFame 对象压⼊矩阵对象
void PushMatrix(GLFame &frame);
//出栈（出栈指的是移除顶部的矩阵对象）
void GLMatrixStack::PopMatrix(void);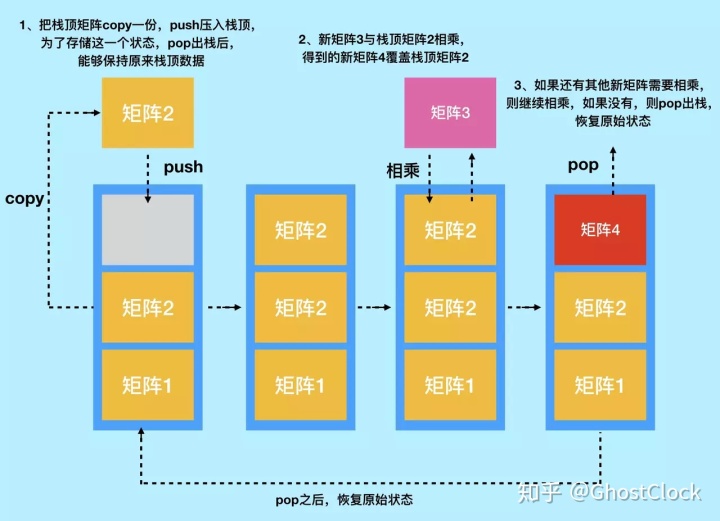
4.2.仿射变换：
//Rotate 函数angle参数是传递的度数，⽽不是弧度
void MatrixStack::Rotate(GLfloat angle,GLfloat x,GLfloat y,GLfloat z);
void MatrixStack::Translate(GLfloat x,GLfloat y,GLfloat z);
void MatrixStack::Scale(GLfloat x,GLfloat y,GLfloat z);4.3.使⽤照相机(摄像机) 和⻆⾊帧进⾏移动
class GLFrame {
protected:
M3DVector3f vOrigin; // Where am I?
M3DVector3f vForward; // Where am I going?
M3DVector3f vUp; // Which way is up?
}4.3.1.GLFrame
//将堆栈的顶部压⼊任何矩阵
void GLMatrixStack::LoadMatrix(GLFrame &frame);
//矩阵乘以矩阵堆栈顶部的矩阵。相乘结果存储在堆栈的顶部
void GLMatrixStack::MultMatrix(GLFrame &frame);
//将当前的矩阵压栈
void GLMatrixStack::PushMatrix(GLFrame &frame);4.4.照相机管理
//GLFrame函数，这个函数⽤来检索条件适合的观察者矩阵
void GetCameraMatrix(M3DMatrix44f m,bool bRotationOnly = flase);案例：
使用模型视图创建投影矩阵
扫一扫
1264
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
