java分治法求数列的最大子段和_数据结构 8 基础排序算法详解、快速排序的实现、了解分治法

快速排序

快速排序与冒泡排序一样，同样是属于 交换排序 叫做快速排序也是有原因的。因为它采用了 分治法的概念

其中最重要的一个概念就是 基准元素

冒泡排序每一轮将一个最大的元素挑选出并移动到右侧。

分治法思想

在每一轮当中。通过 确定基准元素 ，将元素分为两部分，分别大于小于基准元素。而后的一轮中。还是通过 原来 的方式，在这两轮中继续找寻基准元素，直至不可再细分为止。

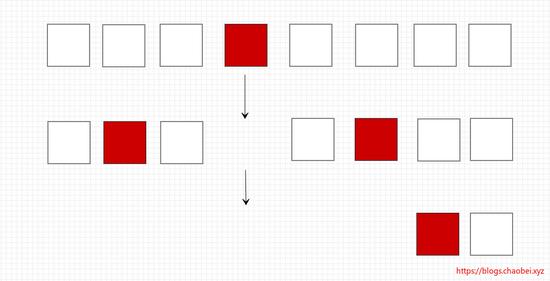
最重要的两个地方：

基准元素的选择 pivot

基准元素的确认一般是选择当前数列的第一个元素,但这种方法确实不太靠谱，一般情况会通过随机选择的方式选择一个基准元素。这样一来，也能避免某些 特殊数列 导致的时间复杂O(N^2);

通过 随机选择 的方式，可以将时间复杂度调整至O(Nlogn);

元素的移动

通过随机的方式选择元素后，接下来就是元素的 移动

移动就是将元素分别移动到基准元素两侧，左侧比基准元素小，右边则比基准元素大。

这里有两种元素的移动方式：

1. 挖坑法
2. 指针交换法

挖坑法

拟定一个无序数列｛4,7,6,5,3,2,9,1｝要求将这个数列从小到大依次排列，我们采用挖坑法进行实现。

挖坑法最重要的地点在于：指定左右指针(left,right)基准元素下标index。基准元素Pivot.

假设我们通过随机法选择 基准元素Pivot = 4 它的 下标index=1 表示一个坑,并且选择了左右的指针 left/right 。

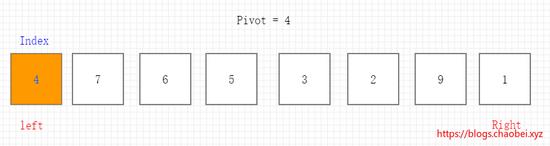
1、从右边指针 right 开始 和基准元素进行比较。若右指针元素大于基准元素，则指针向下移动一位。若小于则将这个元素填入坑里面。将坑的位置记录下来。

此时我们的右边指针元素 1<4 则将右边指针元素 1 填入首位的坑 index 里面。这个时候因为1已经跑到首位去了。所以当前的位置就又成为了一个新的坑，接下来要操作左边指针 left 将左边指针移动一位。如下图所示

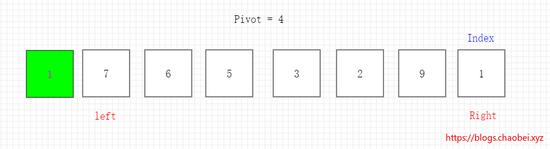
2、开始操作左指针 left

通过比较 7>4 则移动元素，将7移动到坑里面。移动完后，原位置又变成一个新的坑。下面需要操作右边指针，将右边指针移动一位。如下图所示

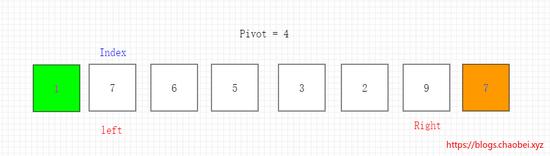
3、按照这样的思路。再次进行操作右边边指针。

通过比较 9>4 则右边的元素已经大于基准元素。则无需移动位置。将右边指针移动一位即可。继续进行比较。如下图所示

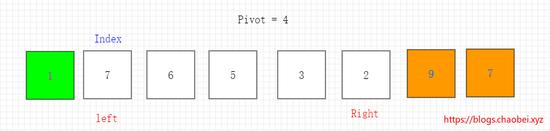
当前右边指针 2<4 则将2填入到坑里面。原位置变成一个坑。左边指针移动一位，交换指针。如下图所示

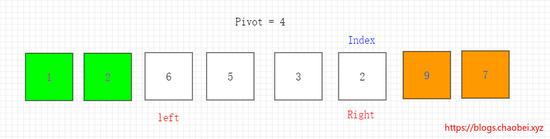
4、继续操作左边指针。

元素 6>4 将元素6移动坑的位置。6位置再次成为一个坑，右边指针移动一位。如下图所示

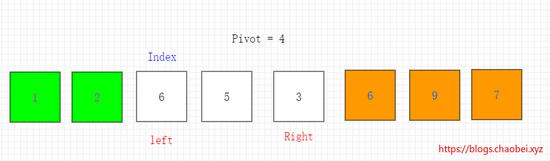
元素 3<4 则将3元素移动到坑的位置。原位置变成坑，左边指针移动一位。如下图所示

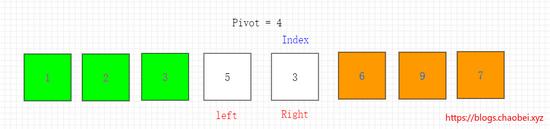
开始操作左边指针 5>4 将5元素移动到坑的位置。右边指针移动一位。发生指针重合。如下图所示

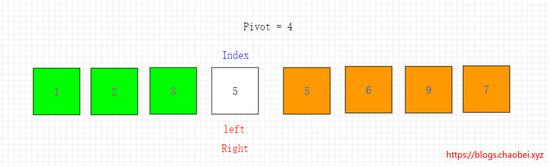
将基准元素移动到重合位置。交换结束。如下图所示

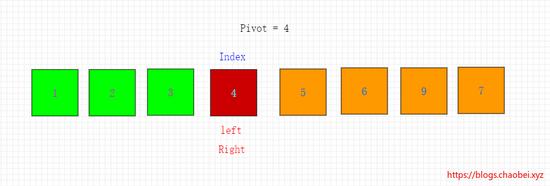
交换总结

1. 左右指针发生元素填坑后才进行交换指针操作(从左指针交换到右指针)
2. 左边指针的元素值大于基准元素则填坑。否则只做移动。
3. 右边指针的元素值小于基准元素则填坑。否则只做移动。
4. 发生填坑后，将另一个指针位置移动一位。
5. 指针重合则结束，将基准元素填充到重合位置。

代码示例

public static void main(String[] args) {        int[] array = {4, 7, 6, 5, 3, 2, 9, 1};        sort(array, 0, array.length - 1);        System.out.println(Arrays.toString(array));    }    public static void sort(int[] array, int start, int end) {        if (start >= end) {            return;        }        int pivotIndex = partition(array, start, end);//通过分治法将数列分成两份，各自再次递归        sort(array, start, pivotIndex - 1);        sort(array, pivotIndex + 1, end);    }    /**     * @return int     * @Author MRC     * @Description 采用分治法 返回基准元素位置     * @Date 17:52 2020/5/25     * @Param [arr 被操作的数组, start 分治法起始位置, end 结束位置]     **/    private static int partition(int[] arr, int start, int end) {        //取首位为基准元素。//也是坑的位置        int pivotIndex = start;        //基准元素的值        int pivot = arr[pivotIndex];        //左边指针        int left = start;        //右边指针        int right = end;        /**         * 大循环用于判断总体循环         * 在左右指针指向同位置后         * 结束循环         */        while (right >= left) {            /**             * 右指针             */            while (right >= left) {                if (arr[right] < pivot) {                    arr[pivotIndex] = arr[right];                    pivotIndex = right;                    left++;                    break;                }                right--;            }            /**             * 左指针             */            while (right >= left) {                if (arr[left] > pivot) {                    arr[pivotIndex] = arr[left];                    pivotIndex = left;                    right--;                    break;                }                left++;            }        }        arr[pivotIndex] = pivot;        return pivotIndex;    }

指针交换法

指针交换法相比于挖坑法，开局还是和挖坑法一样，元素的交换次数更少，效率相比于挖坑法有小幅度的提升。我们来了解一下指针交换法的逻辑。

拿到一个数列 {4, 7, 6, 5, 3, 2, 9, 1}

我们定义左指针 left 右指针 right 以及首位取出的基准元素 pivot=4

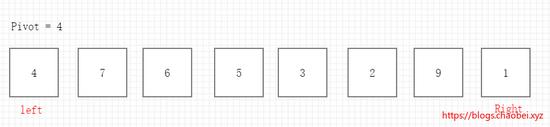
交换要点

1. 从右指针开始循环
2. 右指针指向的元素 大于等于 基准元素，则右指针向左移动一位。 小于 则指针停下。换到左边指针操作。
3. 左指着指向的元素 小于等于 基准元素，则左指针向右移动一位。 大于 则指针停下、跳出循环。
4. 左指针停下后开始交换两个指针位置的元素。开始下次循环。
5. 指针重合大循环结束。重合位置和基准元素进行交换。

详细解说

1、第一次循环

右指针指向元素 1小于4 则右边指针 不移动 交换到左边指针，左边指针指向的元素 4小于等于4(基准元素) 将左边指针移动一位。

当前指针指向元素 7>4 指针停下。

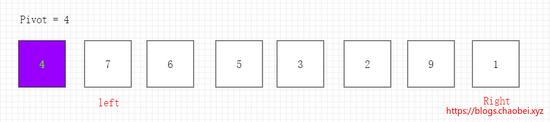
指针停下、开始交换元素。将左右指针位置的元素进行交换

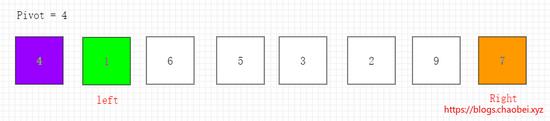
2、第二次循环

重新到右指针，当前 7>4 左移一位。

到达 9 当前 9>4 左移一位。

到达 2 当前 2<4 右边指针停下。

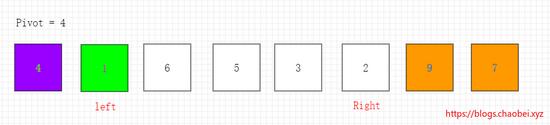
左指针，当前 1<4 右移一位。

到达 6 当前 6>4 左边指针停下。

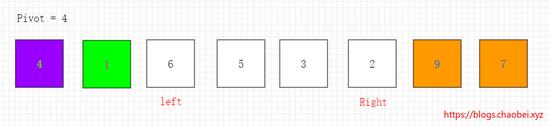
交换两个位置的元素

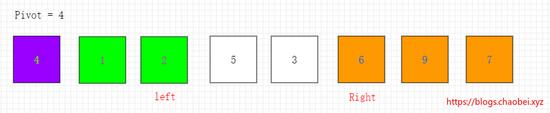
3、第三次循环

右边指针移动到3停下

左边指针移动到5停下

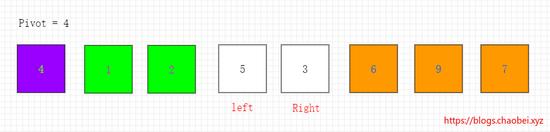
开始交换元素。

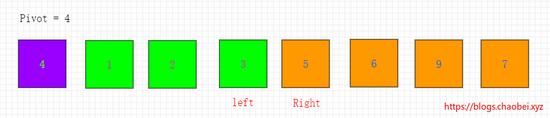
4、第四次循环

移动右指针，已经发生指针的重合，则将重合的位置的元素和基准元素进行交换。

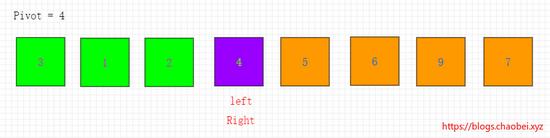
代码示例

public static void main(String[] args) {        int[] array = {4, 7, 6, 5, 3, 2, 9, 1};        sort(array, 0, array.length - 1);        System.out.println(Arrays.toString(array));    }    private static void sort(int[] array, int start, int end) {        if (start >= end) {            return;        }        int pivotIndex = partition(array, start, end);        sort(array, start, pivotIndex - 1);        sort(array, pivotIndex + 1, end);    }    private static int partition(int[] array, int start, int end) {        //取首位为基准元素。//也是坑的位置        int pivotIndex = start;        //基准元素的值        int pivot = array[pivotIndex];        //左边指针        int left = start;        //右边指针        int right = end;        while (right != left) {            /**             * 操作右指针             */            while (right > left && pivot < array[right]) {                right--;            }            /**             * 操作左指针             */            while (right > left && pivot >= array[left]) {                left++;            }            /**             * 交换元素             */            if (right > left) {                int item = array[right];                array[right] = array[left];                array[left] = item;            }        }        /**         * 交换指针位置和基准元素         */        array[pivotIndex] = array[left];        array[left] = pivot;        return left;    }

小结

通过本节，我们研究了快速排序的两种实现方式。我们通过递归的方式实现分治法。通过挖坑交换元素和指针交换的方式分别实现快速排序。快速排序还是一个很重要的排序方法。通过本节的学习。应该了解到 分治法 这个重要的思想