lisp直线连接圆象限电_中考数学最值--辅助圆

动点最值问题，由于是动态问题，因此存在最值。前面我们学过了将军饮马，动点就是直线上需要找的那个点，它的轨迹是一条直线，但是实际题目中，有些动点的轨迹它不是直线，而是一个圆，或者是一段圆弧。需要注意的一点是，题目一般不会直接告诉我们动点的轨迹，而是要求我们利用条件去找到动点的轨迹，那么接下来我们会学习一下最值问题辅助圆的构造方法。

一、利用圆的定义构造轨迹圆

圆的定义：平面内到定点的距离等于定值的所有点构成的集合．

构造思路：若动点到平面内某定点的距离始终为定值，则其轨迹是圆或圆弧．

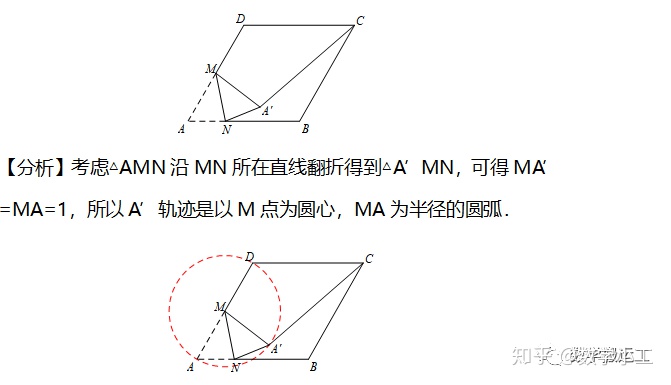
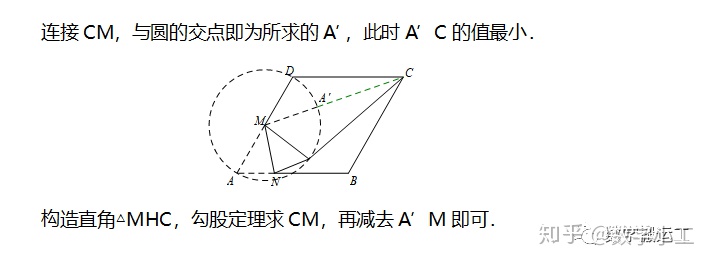
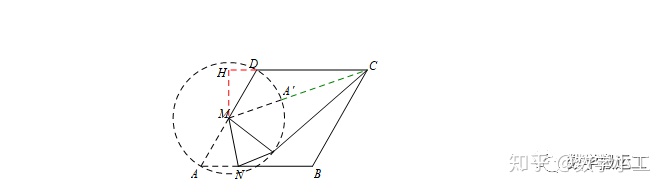
例题1：如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A’MN，连接A’C，则A’C长度的最小值是__________．

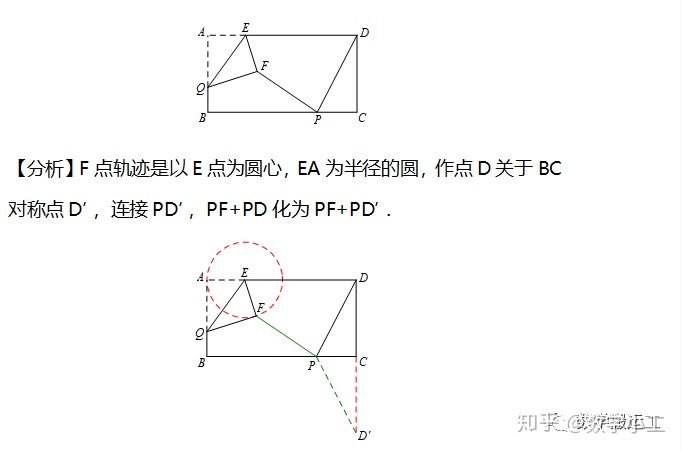
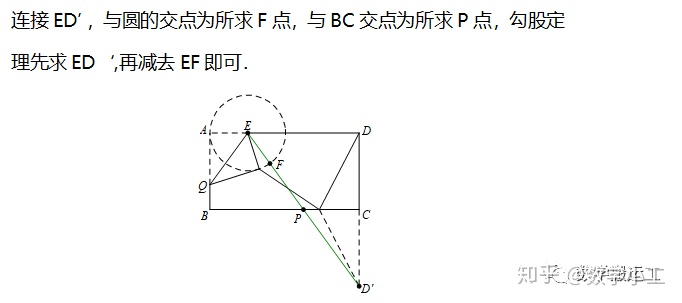
例题2：如图，矩形ABCD中，AB=4，BC=8，P、Q分别是直线BC、AB上的两个动点，AE=2，△AEQ沿EQ翻折形成△FEQ，连接PF、PD，则PF+PD的最小值是_________．

二、利用定边对直角构造辅助圆

知识点：直径所对的圆周角是直角．

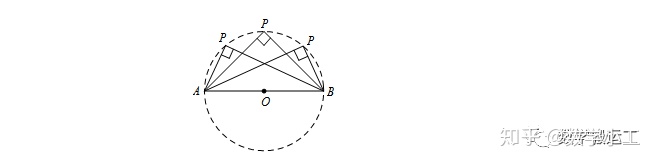
构造思路：一条定边所对的角始终为直角，则直角顶点轨迹是以定边为直径的圆或圆弧．

若AB是一条定线段，且∠APB=90°，则P点轨迹是以AB为直径的圆．

【例题】已知正方形ABCD边长为2，E、F分别是BC、CD上的动点，且满足BE=CF，连接AE、BF，交点为P点，则PD的最小值为_________．

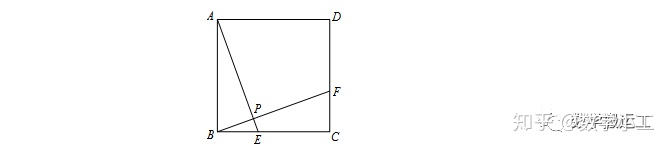
【分析】由于E、F是动点，故P点也是动点，因而存在PD最小值这样的问题，那P点轨迹如何确定？

考虑BE=CF，易证AE⊥BF，即在运动过程中，∠APB=90°，故P点轨迹是以AB为直径的圆．

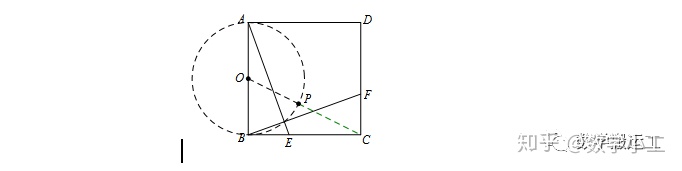
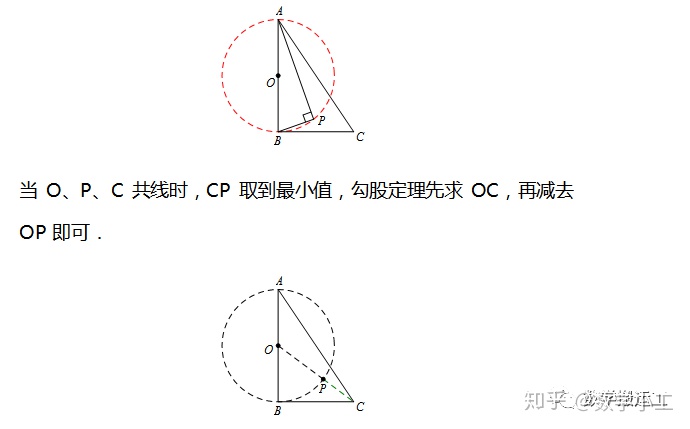
连接OC，与圆的交点即为P点，再通过勾股定理即可求出PC长度．

思路概述：分析动点形成原理，通常“非直即圆”（不是直线就是圆），接下来可以寻找与动点相关有无定直线与定角．

【2013武汉中考】如图，E、F是正方形ABCD的边AD上的两个动点，满足AE=DF，连接CF交BD于点G，连接BE交AG于点H，若正方形边长为2，则线段DH长度的最小值是________．　

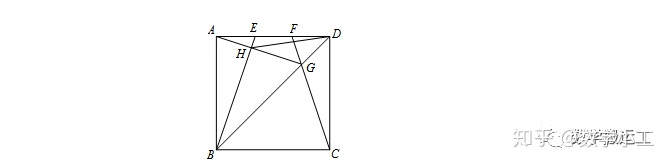
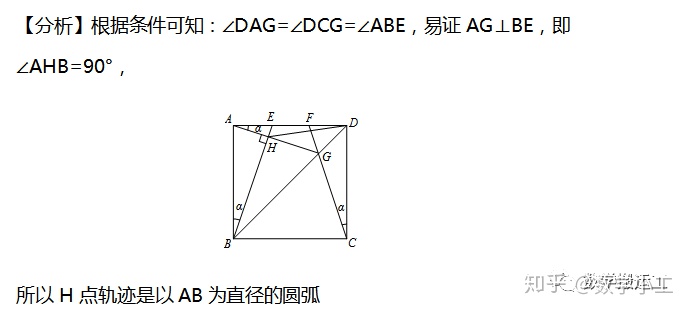
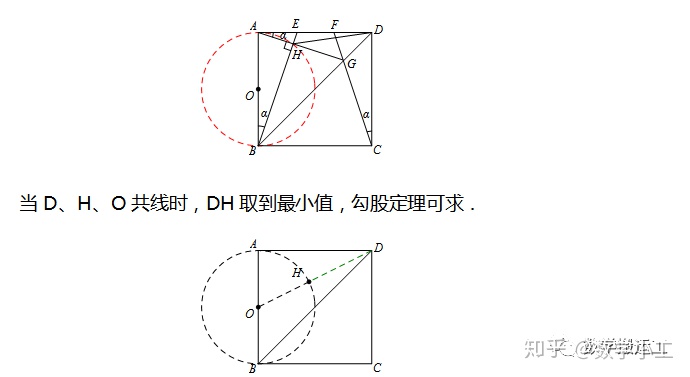
【2016安徽中考】如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值是_________．

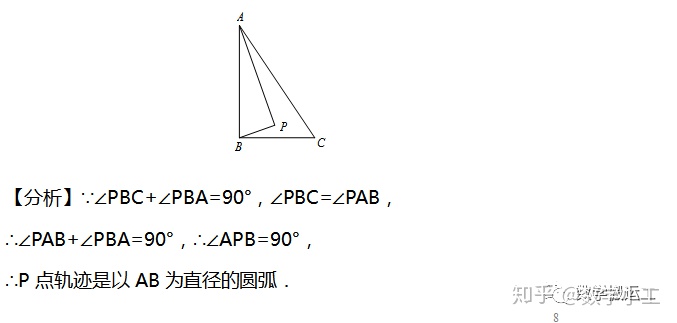
三、定边对定角

在“定边对直角”问题中，依据“直径所对的圆周角是直角”，关键性在于寻找定边、直角，而根据圆周角定理：同圆或等圆中，同弧或等弧所对的圆周角都相．定边必不可少，而直角则可一般为定角．例如，AB为定值，∠P为定角，则A点轨迹是一个圆．

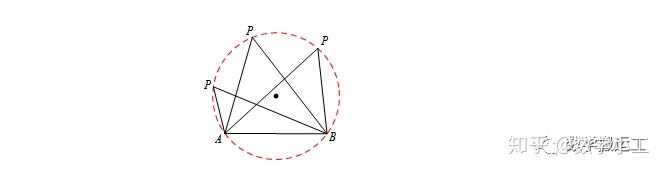
当然，∠P度数也是特殊角，比如30°、45°、60°、120°，下分别作对应的轨迹圆．

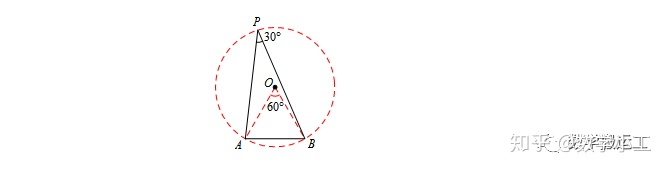
若∠P=30°，以AB为边，同侧构造等边三角形AOB，O即为圆心．

若∠P=45°，以AB为斜边，同侧构造等腰直角三角形AOB，O即为圆心．

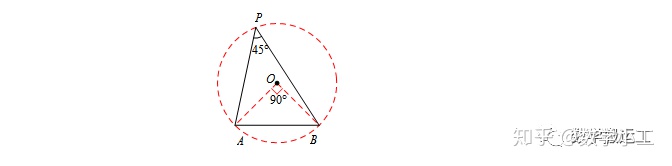
若∠P=60°，以AB为底，同侧构造顶角为120°的等腰三角形AOB，O即为圆心．

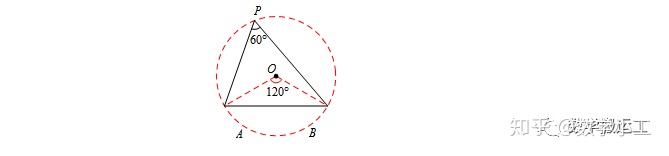
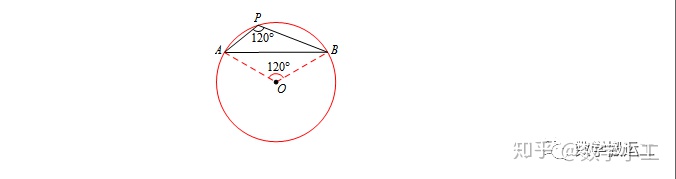
若∠P=120°，以AB为底，异侧为边构造顶角为120°的等腰三角形AOB，O即为圆心．

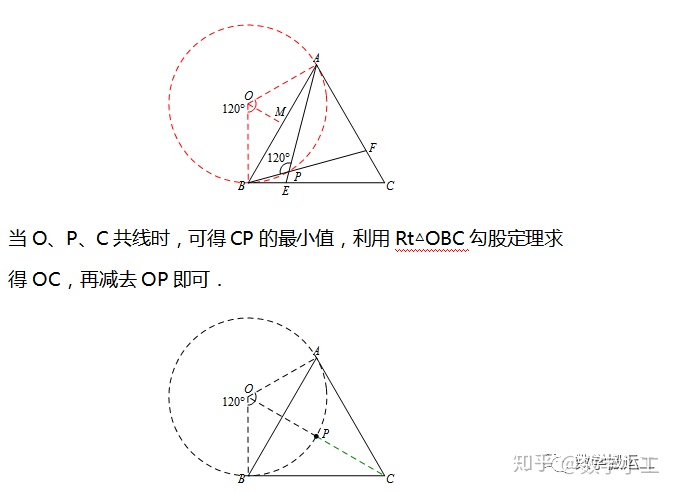
【例题】如图，等边△ABC边长为2，E、F分别是BC、CA上两个动点，且BE=CF，连接AE、BF，交点为P点，则CP的最小值为________．

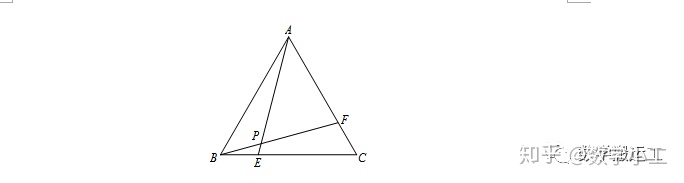
【分析】由BE=CF可推得△ABE≌△BCF，所以∠APF=60°，但∠APF所对的边AF是变化的．

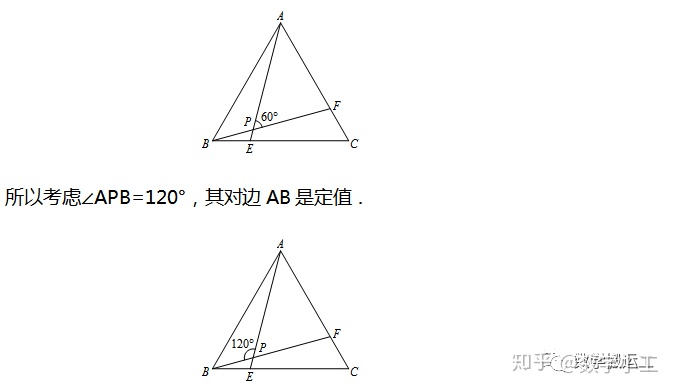
所以如图所示，P点轨迹是以点O为圆心的圆弧．（构造OA=OB且∠AOB=120°）