动态规划是运筹学的一个分支,是求解多阶段决策过程最优化问题的数学方法,在经济管理、工程技术、工农业生产及军事部门中都有着广泛的应用,并且获得了显著的效果。学习动态规划,我们首先要了解多阶段决策问题。
多阶段决策问题例子:
最短路径问题
背包问题
生产决策问题:企业在生产过程中,由于需求是随时间变化的,因此企业为了获得全年的最佳生产效益,就要在整个生产过程中逐月或逐季度地根据库存和需求决定生产计划。
机器负荷分配问题:某种机器可以在高低两种不同的负荷下进行生产。要求制定一个五年计划,在每年开始时,决定如何重新分配完好的机器在两种不同的负荷下生产的数量,使在五年内产品的总产量达到最高。
航天飞机飞行控制问题:由于航天飞机的运动的环境是不断变化的,因此就要根据航天飞机飞行在不同环境中的情况,不断地决定航天飞机的飞行方向和速度(状态),使之能最省燃料和完成飞行任务(如软着陆)。
多阶段决策过程的特点:
根据过程的特性可以将过程按空间、时间等标志分为若干个互相联系又互相区别的阶段。
在每一个阶段都需要做出决策,从而使整个过程达到最好的效果。
各个阶段决策的选取不是任意确定的,它依赖于当前面临的状态,又影响以后的发展。
当各个阶段的决策确定后,就组成了一个决策序列,因而也就决定了整个过程的一条活动路线,这样的一个前后关联具有链状结构的多阶段过程就称为多阶段决策问题。
针对多阶段决策过程的最优化问题,美国数学家Bellman等人在20世纪50年代初提出了著名的最优化原理,把多阶段决策问题转化为一系列单阶段最优化问题,从而逐个求解,创立了解决这类过程优化问题的新方法:动态规划。
对最佳路径(最佳决策过程)所经过的各个阶段,其中每个阶段始点到全过程终点的路径,必定是该阶段始点到全过程终点的一切可能路径中的最佳路径(最优决策),这就是Bellman提出的著名的最优化原理。即 一个最优策略的子策略必然也是最优的。
A地到 E 地要铺设一条煤气管道,其中需经过三级中间站,两点之间的连线上的数字表示距离。如图所示,问应该选择什么路线,使总距离最短?
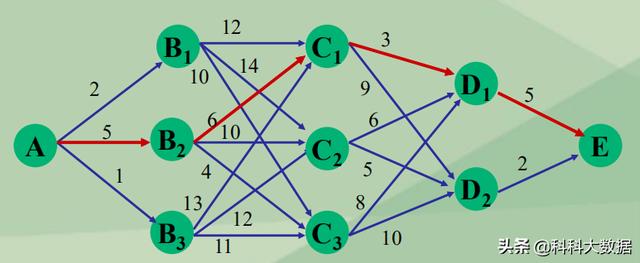
解:整个计算过程分为四个阶段,从最后一个阶段开始。
第四阶段:有两条路。 ①D1E=5,②D2E=2。②最优。
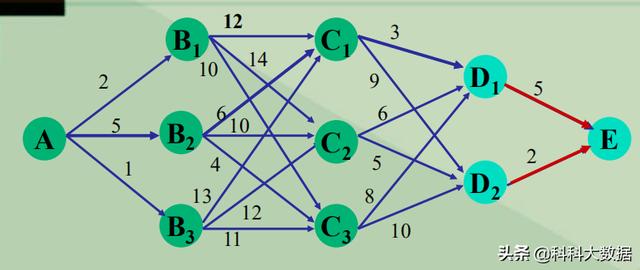
第三阶段:有六条路。
经过C1点——①C1D1+5=8,②C1D2+2=11。 ①最优。
经过C2点——①C2D1+5=11,②C2D2+2=7。 ②最优。





 动态规划是一种运筹学方法,用于解决多阶段决策过程的最优化问题,如最短路径、背包问题和生产决策等。通过对问题进行分阶段处理,动态规划将复杂问题分解为一系列单阶段最优化问题,逐步求解。文章通过实例解释了动态规划的求解步骤和最优化原理,并介绍了投资分配和背包问题的具体应用。
动态规划是一种运筹学方法,用于解决多阶段决策过程的最优化问题,如最短路径、背包问题和生产决策等。通过对问题进行分阶段处理,动态规划将复杂问题分解为一系列单阶段最优化问题,逐步求解。文章通过实例解释了动态规划的求解步骤和最优化原理,并介绍了投资分配和背包问题的具体应用。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








