
第七章 图
图这一章内容很多,所以会分几篇文章记录
7.2 图的定义
图是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V, E),其中G表示一个图,V是图G中顶点的集合,E是图G中边的集合

注意的是:
图中的数据元素,我们称之为顶点(Vertex),而且在图中,我们强调不能没有顶点,定义也中强调了顶点的集合为非空集合。
图中的任意两个顶点都有可能存在关系,逻辑关系使用边来表示,边的集合可以是空集
7.2.1 各种图的定义
无向边:若顶点vi到vj之间的边没有方向,则称这条边为无向边,用无序偶对(vi, vj)来表示。如果图中任意顶点之间的边都是无向边,则整个图就是无向图
有向边:若从顶点vi到顶点vj的边有方向,则称这条边为有向边,也成为弧。弧用有序偶对<vi, vj>来表示,vi称为弧尾,vj称为弧头(有向边箭头所指的方向是弧头,反之是弧尾)。如果图中任意两个顶点之间的边是有向边,则该图是有向图

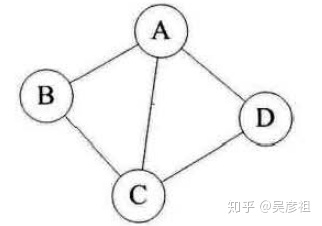
在图中,若不存在顶点到自身的边,且同一条边不会重复出现,则称这样的图为简单图
下面就不是简单图

无向图中,若任意顶点之间都存在边,则称该图是无向完全图。含有n个顶点的无向完全图有[n * (n - 1)] / 2条边
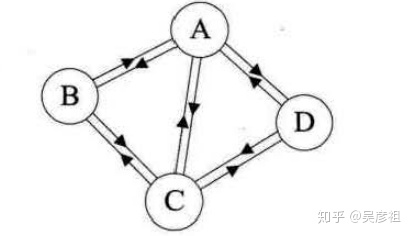
下面这张图就是无向完全图

在有向图中,任意两个顶点之间都存在方向弧尾相反的两条弧,则称该图为有向完全图。还有n个顶点的有向完全图中存在n * (n - 1)条弧
有些图的边或者弧具有与他相关的数字,这种与图的边或弧相关的数叫做权,这些劝可以表示从一个顶点到另一个顶点的距离或者耗费,这种带权的图通常被称之为网

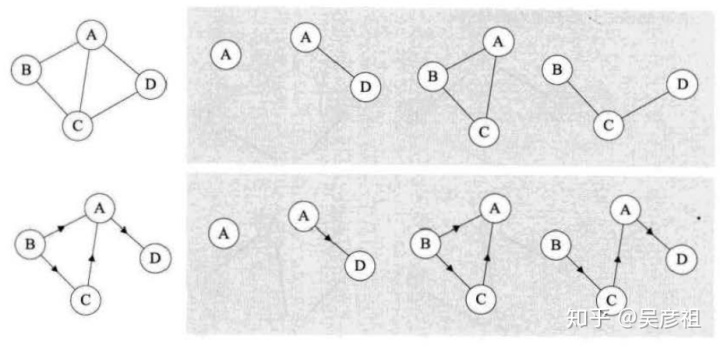
假设两个图G = (V, {E})和G' = (V', {E'}),如果V'属于V,E'属于E,则称G'为G的子图
7.2.2 图的顶点与边间的关系
对于无向图G = (V, {E}),如果边(v, v')属于E,则称顶点v与v'互为邻接点,即v与v'相邻接,边(v, v')依附于顶点v和v'。顶点v的度就是和v相关联的边的数目,记为TD(v)。边数就是各顶点的度数和的一半
对于有向图,以v为弧头的弧的数目称为v的入度ID(v),以v为弧尾的弧的数目称为v的出度OD(V),所以顶点v的度TD(v) = ID(v) + OD(v)
图中任意两点之间的路径为该路径上一系列顶点的序列,当然如果是有向图,则路径也是有方向的,注意图中顶点到顶点之间的路径不是唯一的


路径的长度是路径上边或者弧的数目
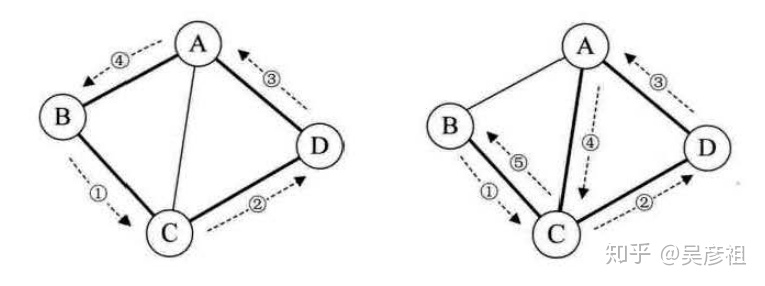
第一个顶点到最后一个顶点相同的路径称为回路或者环。序列中顶点不重复出现的路径称之为简单路径。除了第一个顶点和最后一个顶点,其余顶点不重复出现的回路,称为简单回路或者简单环
下图中的左图就是简单环,右图则不是
7.2.3 连通图相关术语
在无向图中,如果顶点vi到顶点vj之间存在路径,则说明两个顶点是连通的。对于同中的任意两个顶点,如果都是连通的,则说明该图是连通图,无向图中的极大连通子图称之为连通分量
下图中的左图就是非连通图,右图是连通图

在有向图中,任意两个顶点之间都存在路径,则说明该图为强连通图,有向图中的极大强连通子图为有向图的强连通分量

连通图的生成树是一个极小的连通子图,它含有图中的全部n个顶点,但只足以构成一棵树的n-1条边
如果一个图有n个顶点和小于n-1条边,则是非连通图,如果多于n-1条边,必定构成一个环。但是有n-1条边,不一定能构成生成树
其实可以想象,如果有n个顶点,每个顶点之间只有一条边,则正好是n-1条边,如果再多一条边,则就存在度为2的顶点,可以构成一个回路
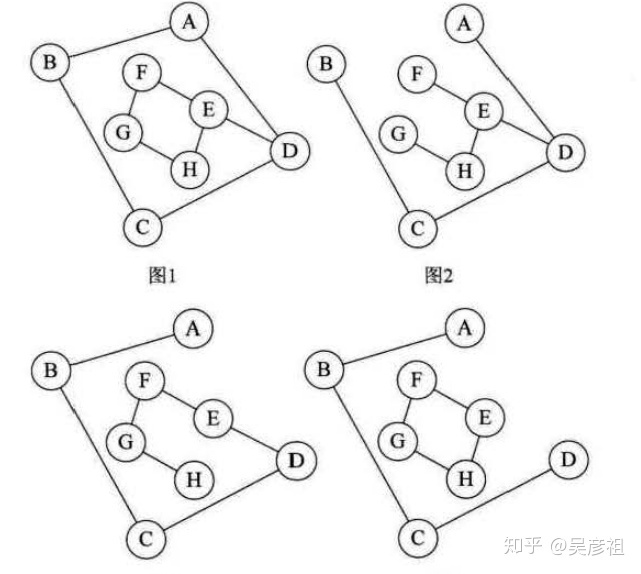
如果一个有向图中存在一个入度为0的顶点,而其他顶点的入度为1,则则是一棵有向树。入度为0的顶点有向树的根结点,其他顶点为树的结点
7.3 图的抽象数据类型

7.4 图的存储结构
图的村树结构有两种,一种是邻接矩阵,另一种是邻接表
7.4.1 邻接矩阵
邻接矩阵存储方式使用两个数组来表示图。一个一维数组存储图的顶点信息。另一个二维数组(邻接矩阵)存储图的边或弧的信息
设图G有n个顶点,则邻接矩阵就是一个n阶的方阵,定义为

举个栗子
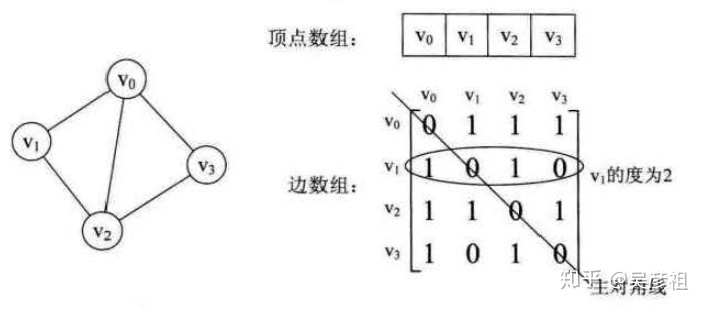
上述是一个无向图,其中二维数组就是邻接矩阵,若两个顶点之间存在边,则矩阵总元素为1,否则如果两顶点之间没有边,则元素为0。无向图的邻接矩阵是一个对称矩阵
从图中我们可以得知:
1、两个顶点之间是否有边
2、计算出某个顶点的度,为该顶点所在行中的元素之和
3、某顶点的邻接顶点就是该顶点所在行中元素为1的顶点比如图中v1的邻接点是v0和v2
我们再来看看有向图的邻接矩阵

我们发现有向图的邻接矩阵并不是对称矩阵,而且顶点vi的入度为第vi列各数之和,顶点vi的出度为第vi行的各数之和
在图的术语中,我们还提到了网的概念,怎么样才能用邻接矩阵讲网中的权值也保存下来呢?
我们假设G是网图,有n个顶点,则邻接矩阵是一个n阶方阵,我们能有如下定义:

其中Wij是vi与vj之间的权值,若两不同顶点之间没有关系,我们就用无穷大来表示,这样可以与权值进行区分

下面我们来看一下邻接矩阵的实现,我因为学的是python,所以用的是python代码来实现,网上基本是c++和java的代码,可以自行查阅
#邻接矩阵的实现
class Graph(object):
#mat是图的二维矩阵的表示
#unconn = 0,表示两顶点之间无边(无联系)
def __init__(self, mat, unconn = 0):
vnum = len(mat) #顶点个数
for x in mat: #判断该二维数组是否为方阵
if len(x) != vnum:
raise ValueError("Argument for 'Graph'.")
self._mat = [mat[i][:] for i in range(vnum)] # 将图方阵进行拷贝
self._unconn = unconn
self._vnum = vnum
def vertex_num(self): #获取顶点个数
return self._vnum
def _invalid(self, v): #判断顶点是否有效
return v >= self._vnum or v < 0
def add_vertex(self): #增加顶点
raise GraphError("Adj-Matrix dose not support 'add_vertex'.")
def add_edge(self, vi, vj, val = 1): #增加边
if self._invalid(vi) or self._invalid(vj):
raise GraphError(str(vi) + "or" + str(vj) + "is not valid vertex.")
self._mat[vi][vj] = val
def get_edge(self, vi, vj): #获取边
if self._invalid(vi) or self._invalid(vj):
raise GraphError(str(vi) + "or" + str(vj) + "is not valid vertex.")
return self._mat[vi][vj]
def out_edges(self, vi): #获取该顶点的出边
if self._invalid(vi):
raise GraphError(str(vi) + "id not valid vertex.")
return self._out_edges(self._mat[vi], self._unconn)
@staticmethod
def _out_edges(row, unconn): #传入一行,该行为一个顶点与其他顶点之间的权值,unconn表示无权值,即两顶点之间无联系
edges = [] #创建列表,存储出边
for i in range(len(row)): #遍历该顶点与其他顶点的权值,如果权值不为0,则将与之相连的顶点和权值组成元组添加至出边列表中
if row[i] != unconn:
edges.append((i, row[i]))
return edges7.4.2 邻接表
邻接矩阵虽然是一种不错的存储结构,但是在某些情况下会造成资源的浪费,比如说下面这种情况

我们发现,邻接矩阵中只有一个元素有权值,对空间造成了极大的浪费,所以我们考虑了邻接表这一形式
我们把链表和数组相结合的存储方法称为邻接表
邻接表的处理方法如下:
1、首先用一个数组存储顶点信息,每个数据元素不仅存储了该顶点的信息,还存储了指向第一个邻接点的指针
2、图中每个顶点vi的所有邻接点构成一个线性表,由于邻接点的个数不确定,所以用单链表进行存储如下图所示,adjvex是邻接点域,存储某顶点的邻接点在顶点表中的下标

有向图由于是有方向的,我们是以顶点为弧尾来存储边的,这样很容易就可以得到每个顶点的出度

反之,也可以以顶点为弧头来存储边,可以很容易得到顶点的入度
对于带权值的网图,可以在边表节点定义中再增加一个权值的数据域,存储权值信息
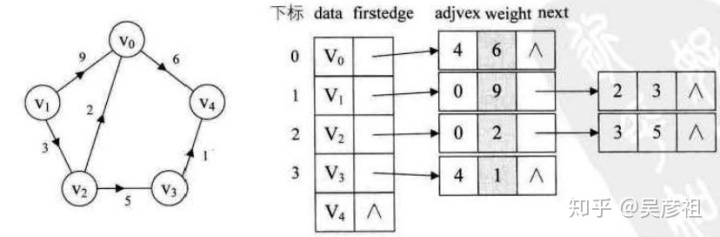
#邻接表的实现
#继承了邻接矩阵的out_edge()方法
class GraphAL(object):
def __init__(self, mat = [], unconn = 0):
vnum = len(mat)
for x in mat:
if len(x) != vnum:
raise ValueError("Argument for 'GraphAL'.")
#此时的self._mat描述的是各个顶点的出边,是一个二维矩阵,其中每一个元素都是一个由相邻顶点和其权值组成的元组
self._mat = [Graph.out_edges(mat[i], unconn) for i in range(vnum)]
self._vnum = vnum
self._unconn = unconn
def add_vertex(self): #增加顶点
self._mat.append([])
self._vnum += 1
return self._vunm
def add_edge(self, vi, vj, val = 1): #增加边
if self._invalid(vi) or self._invalid(vj):
raise GraphError(str(vi) + "or" + str(vj) + "is not valid vertex.")
if self._vnum == 0:
raise GraphError("Cannot add edge to empty graph.")
#row为顶点vi与其他顶点之间的权值,是一个一维数组。其元素为由相邻顶点和其权值构成的元组
row = self._mat[vi]
i = 0
#设置i,来遍历vi的所有相邻点
while i < len(row):
#假如没有遍历到vj这个相邻点,则退出循环,在row最后增加该相邻点vj及其权值
if row[i][0] != vj:
break
#假如遍历到vj这个相邻点,直接修改其权值
if row[i][0] == vj:
self._mat[vi][vj] = val
return
i += 1
self._mat[vi].insert(i, (vj, val))
def get_edge(self, vi, vj): #获得边
if self._invalid(vi) or self._invalid(vj):
raise GraphError(str(vi) + "or" + str(vj) + "is not valid vertex.")
#遍历vi的所有相邻点和其权值,分别用i和val保存
#当遍历到vj这个顶点时,返回其权值
#如果没有遍历到vj,返回self._unconn,表示两顶点无联系
for i, val in self._mat[vi]:
if i == vj:
return val
return self._unconn
def out_edges(self, vi): #返回vi顶点的出边
if self._invalid(vi) or self._invalid(vj):
raise GraphError(str(vi) + "or" + str(vj) + "is not valid vertex.")
return self._mat[vi]7.5 图的遍历
从图中某一顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次,这一过程叫做图的遍历
7.5.1 深度优先遍历(DFS)与广度优先遍历(BFS)
DFS遍历主要用的是栈,BFS用的是队列
推荐b站大神“正月点灯笼”的详细讲解视频,一看就懂详解DFS和BFS
#深度遍历
def DFS(graph, s):
#graph是图,s是起始点
stack = [] #创建栈,用于存放顶点
stack.append(s)
seen = set() #创建集合,存放已遍历过的顶点
seen.add(s)
while len(stack) > 0: #当栈中存在数据时,取出最后一个数据,直到栈为空栈时停止遍历
vertex = stack.pop()
nodes = graph._mat[vertex] #nodes为vertex相邻点及其权值的集合,是一个一维数组,元素为元组
for w in nodes: #遍历每一个相邻点,如果点还没有遍历,则将该点存入栈中,且存入遍历点集合中
if w[0] not in seen:
stack.append(w[0])
seen.add(w[0])
print(vertex)
#广度遍历
def BFS(graph, s):
#graph是图,s是起始点
queue = [] #创建队列,用于存放顶点
queue.append(s)
seen = set() #创建集合,存放已遍历过的顶点
seen.add(s)
while len(queue) > 0: #当队列中存在数据时,取出第一个数据,直到队列为空队列时停止遍历
vertex = queue.pop(0)
nodes = graph._mat[vertex] #nodes为vertex相邻点及其权值的集合,是一个一维数组,元素为元组
for w in nodes: #遍历每一个相邻点,如果点还没有遍历,则将该点存入队列中,且存入遍历点集合中
if w[0] not in seen:
queue.append(w[0])
seen.add(w[0])
print(vertex)






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








