c语言开口向下的标志邻接表,C语言实现邻接表的普里姆算法（完整代码）

今天我用C语言来实现下面的图的最小生成树：

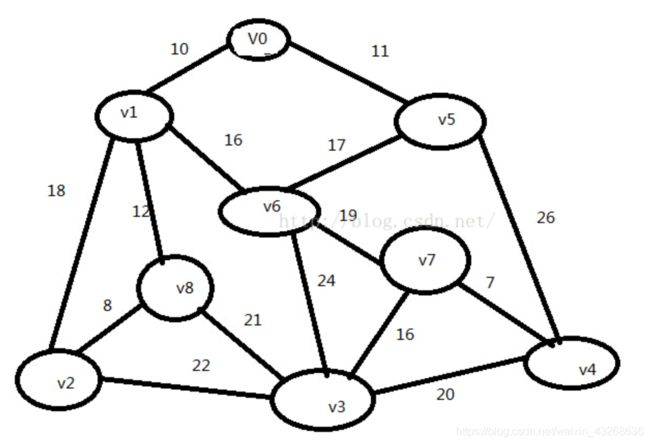
它的最小生成树为：

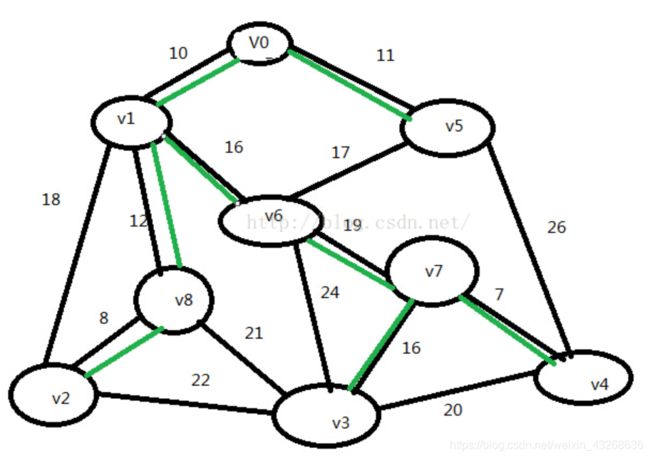
最小生成树的思路是：先从一个顶点出发，把它加入集合V中，从与它相连接的边中找到权值最小的边，与权值最小的边的另一个顶点作为起始点，加入集合V中，再从集合V中顶点中找出未遍历的权值最小的边，找出与它的相连的另一顶点再作为起始点，以此类推下去，最小生成树就形成了。

首先我们先创建邻接表

预定义

#define MaxVertexNum 100

int MAX=0;

typedef int VertexType;

typedef struct node//定义相连接的顶点与权值

{

int adjvex;

int lowcost;

struct node *next;

}EdgeNode;

typedef struct//定义顶点

{

int vertex;

EdgeNode *firstedge;

}VertexNode;

typedef VertexNode AdjList[MaxVertexNum];//定义100个顶点

typedef struct//图的顶点数量为n,边数为e.

{

AdjList adjlist;

int n,e;

}ALGraph;

struct

{

int adjvex;

int lowcost;

}compare[MaxVertexNum]; //记录访问过的顶点

创建邻接表

int localN(ALGraph *G,int m)//查找顶点的下标

{

int i;

for(i=0;in;i++)

{

if(G->adjlist[i].vertex==m)

{

return i;

}

}

return -1;

}

void create(ALGraph *G)//创建邻接表

{

int i,j,k,m;

EdgeNode *s;

printf("读入顶点和边数");

scanf("%d %d",&G->n,&G->e);

for(i=0;in;i++)

{

printf("建立顶点表");

fflush(stdin);

scanf("%d",&G->adjlist[i].vertex);

G->adjlist[i].firstedge=NULL;

}

printf("建立边表\n");

for(k=0;ke;k++)

{

printf("读入(vi-vj)的顶点对序号和之间的权值");

scanf("%d %d %d",&i,&j,&m);

if(m>MAX)//找出最大的权重

{

MAX=m;

}

i=localN(G,i);

j=localN(G,j);

s=(EdgeNode*)malloc(sizeof(EdgeNode));

s->adjvex=j;

s->lowcost=m;

s->next=G->adjlist[i].firstedge;

G->adjlist[i].firstedge=s;

s=(EdgeNode*)malloc(sizeof(EdgeNode));

s->adjvex=i;

s->lowcost=m;

s->next=G->adjlist[j].firstedge;

G->adjlist[j].firstedge=s;

}

MAX++;//制作比最大权重的数还大的数表示为两个顶点没有连通

for(k=0;kn;k++)

{

compare[k].lowcost=MAX;//初始化所有顶点。

}

}

普里姆算法(最小生成树算法)

int FindMin(ALGraph *G)//找到最小的权重的边

{

int i,result=-1;

int min=MAX;

for(i=0;in;i++)

{

if(min>compare[i].lowcost && compare[i].lowcost!=0)

{

min=compare[i].lowcost;

result=i;

}

}

return result;

}

void MinSpanTree_Prim(ALGraph *G,int m)//最小生成树算法

{

int i,j,k,n;

int t1,t2;

EdgeNode *p;

k=localN(G,m);

p=G->adjlist[k].firstedge;

while(p)//与顶点m相连的边的权重和顶点输入compare[]数组

{

i=p->adjvex;

compare[i].adjvex=m;//这里adjvex为与m这个顶点相连的顶点

compare[i].lowcost=p->lowcost;

p=p->next;

}

compare[k].lowcost=0;//访问过的顶点的边权重为0

for(i=1;in;i++)

{

k=FindMin(G);

t1=G->adjlist[k].vertex;

t2=compare[k].adjvex;

printf("%d->%d\n",t2,t1);

compare[k].lowcost=0;

p=G->adjlist[k].firstedge;

while(p)

{

n=p->adjvex;

if(compare[n].lowcost>p->lowcost)//与上个顶点比较，权重小的边输入权重和相连接的顶点

{

compare[n].adjvex=G->adjlist[k].vertex;

compare[n].lowcost=p->lowcost;

}

p=p->next;

}

}

}

主函数：

#include #include int main()

{

ALGraph *G=(ALGraph *)malloc(sizeof(ALGraph));

create(G);

MinSpanTree_Prim(G,0);

EdgeNode *p;

int i;

printf("其邻接表为('->'表示两个之间有连接)：\n");

for(i=0;in;i++)

{

p=G->adjlist[i].firstedge;

printf("%d->",G->adjlist[i].vertex);

while(p!=NULL)

{

printf("%d->",G->adjlist[p->adjvex].vertex);

p=p->next;

}

printf("\n");

}

return 0;

}

运行：输入顶点，输入边和权重。

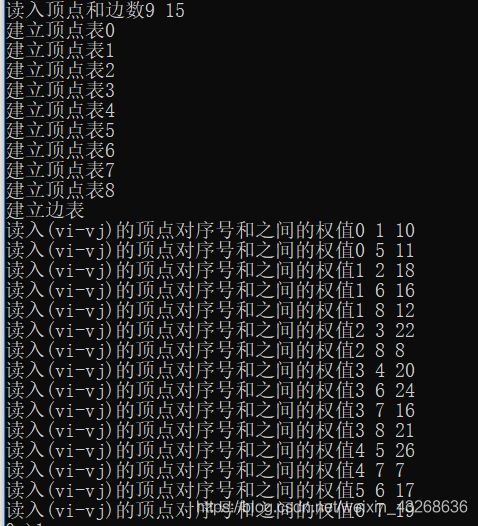
输出最小生成树和邻接表，结果如下：

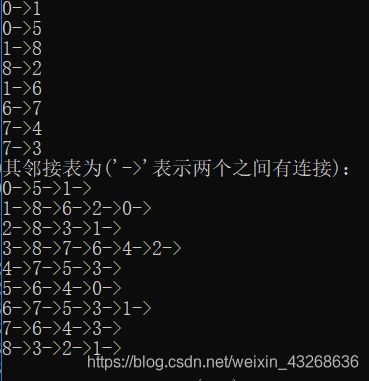
谢谢浏览~，点个赞支持一下呗！谢谢啦！