矩阵为奇异工作精度_矩阵与数值计算（4）——矩阵的奇异值分解

前言

对于方阵，利用其特征值和特征向量可以刻画矩阵的结构。对于长方阵情况，这些方法已经不适用，而推广的矩阵的奇异值分解可以改善这种情况。

矩阵奇异值分解在矩阵理论和数值计算中都有重要应用，以此为基础建立了不少稳定性算法。矩阵的奇异值分解来源于仿射变换将单位球变为椭圆。

我们想将非方阵建立与形如

或

矩阵之间的关系。

建立联系的过程就是对称化，对称化也有不同的计算形式。

对称化

我们思路就是通过

来进行计算。

一、矩阵奇异值分解的几何意义

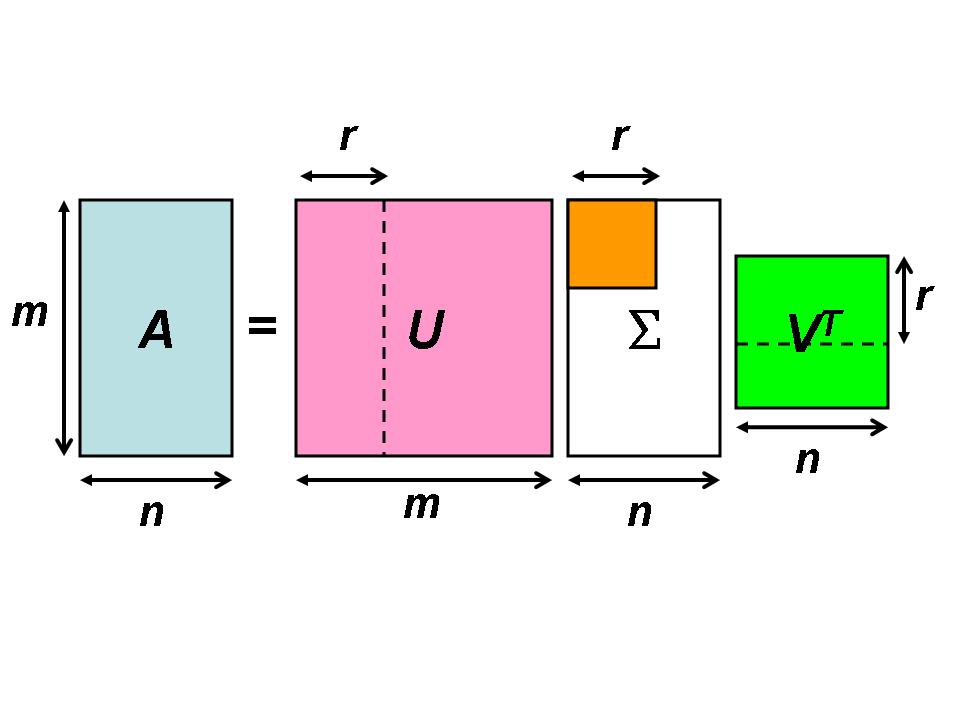
我们先给出矩阵奇异值分解的基本形式

，其中

和

是正交单位矩阵（酉矩阵）。假设当前有一个向量

，其二范数

，有单位圆

，我们有一个变换矩阵

，通过

作用到向量

上，得到新的

，变成了椭圆

。

仿射变换

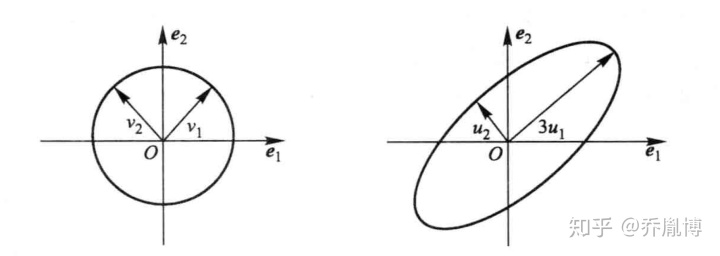
一般来说，

矩阵奇异值分解

二、构造性证明

假设存在A，B矩阵满足，

，我们做一下变换

，则进一步我们计算

如下推导，

，

其中的特征值

是计算出来的特征值，从大到小排列，那么我们进而会得到如下形式

=

=

，则我们可以推导出奇异值分解的构造。

。

三、奇异值分解过程

经过上面的推导，我们知道了奇异值分解的基本形式，矩阵A不一定是满秩矩阵，或矩阵A是一个非方阵，这种情况下，U和V需要进行划分，寻找的划分为如下这种形式。

。

那么继而有

，

那么相应的有，

。

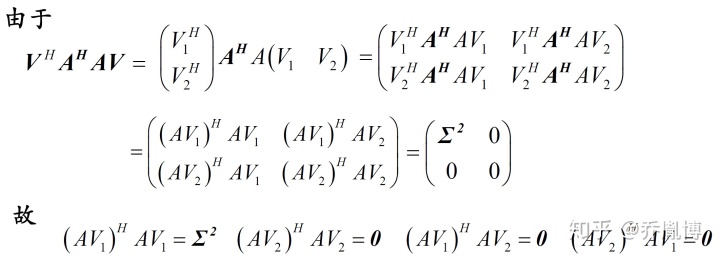
这样我们得到了八个式子，通过这八个式子，我们就可以计算出我们想要的

。

U,V推导

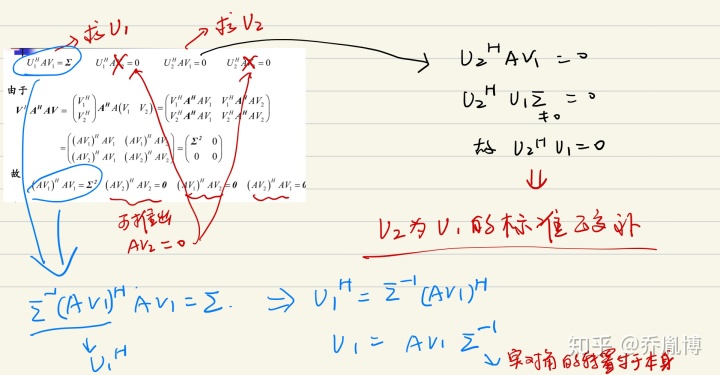
经过上面的公式推导，我们正式提出奇异值分解定理。

奇异值分解定理

其中

是矩阵A的非零奇异值。

里面包含0项，我们进而提出约化奇异值分解。

约化奇异值分解

左右奇异向量

左右奇异向量

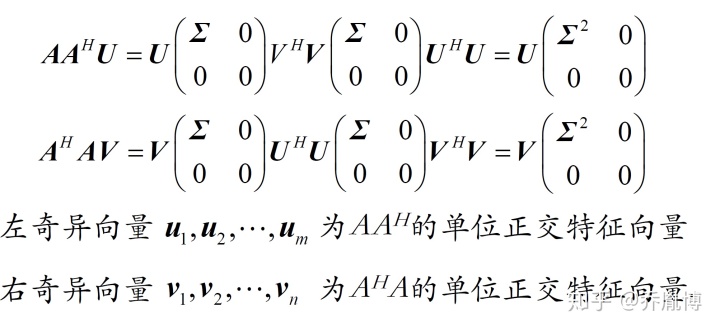
四、奇异值分解讨论矩阵的性质

像空间、零空间

矩阵奇异值与范数、行列式

矩阵奇异值与范数、行列式

总结

奇异值分解是非常重要的分解，在涉及矩阵的计算中被大规模使用。

到此为止，矩阵的三角分解相关知识介绍完毕，接下来将内容将会分享矩阵级数、矩阵幂级数和矩阵微积分的相关知识。