本文深入讲解了八大排序算法，包括冒泡排序、直接插入排序、希尔排序、快速排序、简单选择排序、堆排序、归并排序和基数排序。每种算法都详细介绍了其排序过程、动态流程图和代码实现。
八大排序：
目录
冒泡排序
排序过程：
从第一个往后进行相邻元素遍历，如果前一个元素大于后一个元素，则交换两者的位置，遍历完一轮就能确定最后一个元素为该次遍历总长度的最大值，而且每遍历一轮，下次遍历的元素个数减1，所以对于n个元素的数组，遍历n-1轮完成排序过程，第一轮确定n-1个元素，第二轮确定第n-2个元素......第n-1轮确定第2个元素，第一个元素自然确定了，下图展示了冒泡排序的整个过程：
动态流程图：
代码：
/*冒泡排序*/
class solution
{
public:
vector<int> bubbleSort(vector<int> data)
{
vector<int> result;;
int length=data.length();
int temp=0;
int number=length-1;
result=data;
while(number)
{
/*每循环一次，确定一个元素的位置，而且下一次遍历的个数减1*/
for(int i=0;i<number;i++)
{
if(result[i]>=result[i+1])
{
temp=result[i];
result[i]=result[i+1];
result[i+1]=temp;
}
}
number-=1;
}
return result;
}
}直接插入排序
排序过程：
从第二个元素遍历开始往前插入，具体怎么插入，每次遍历一个元素，都把该元素与前面元素一一比较，比如遍历到第m个元素，比较顺序是从m-1个元素开始往前挨个比较，如果第m个元素小于其中某个元素就互换两者位置，直到没有元素比该元素小，就确定下来该元素的位置。
动态流程图：
代码:
/*插入排序*/
class solution
{
public:
vector<int> directSort(vector<int> data)
{
vector<int> result;
result=data;
int temp=0;
/*从第一个元素开始，没遍历到一个元素，将该元素与前面元素比较，直到前面元素小于该元素为止*/
for(int i=1;i<result.length();i++)
{
int j=i;
while(result[j]<result[j-1]&&j>0)
{
temp=result[j];
result[j]=result[j-1];
result[j-1]=temp;
j--;
}
}
return result;
}
}
希尔排序
排序过程：
希尔排序是建立在冒泡排序基础之上，把数组分成若干份，这若干份是有讲究的，一般取n=n/2或者n=n/3，直到n=1为止，并且在每次分成这么多份后都要对每份进行选择排序，所以分割的数组元素下标的间隔顺序是n，并且随着n越小，每一子数组中的元素个数越多，当n=1时，数组元素最多，进行最后一组选择排序，并且只有一个数组且该数组个数是总的数组个数。下图是该数组的希尔排序的过程，相同颜色的表示一个子数组，并对相同颜色的元素进行选择排序，可以看出相同元素的间距越来越小，也就是n越来越小，最后等于1
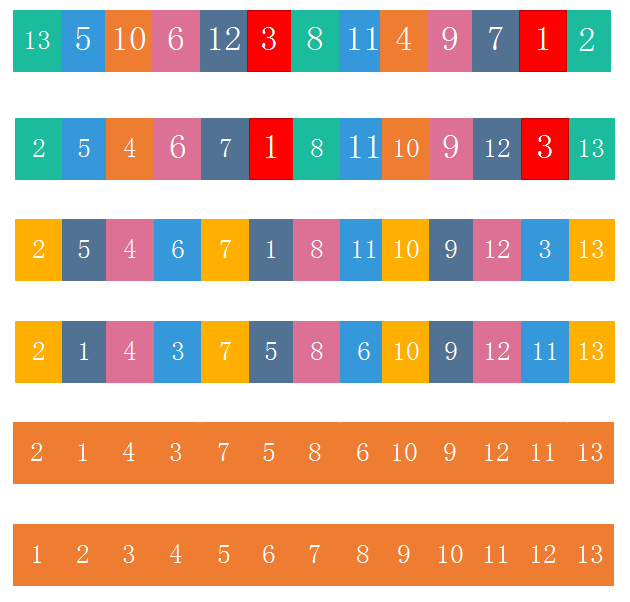
代码：
//@https://blog.51cto.com/13733462/2114341
/*希尔排序*/
class solution
{
public:
vector<int> hillSort(vector<int> data)
{
vector<int> result;
result=data;
int length=data.length();
for(int i=length/2;i>=1;i/=2)
{
/*分成若干个子数组进行插入排序，插入排序，每次的数据量不一定相同，总共i组*/
for(int j=0;j<i;j++)
{
// /*这些数组进行插入排序的顺序*/
// int num=0;
// num=j+i;
// int k=1;
// while(num*k<length)
// {
// k++;
// }
// /*计算得到数组的最大下标,并且该数组的下标以i为间隔*/
// int n=num*(k-1);
/*进行插入排序,每次插入排序的数组从第二个元素开始往前比较*/
for(int p=j+i;p<length;p+=i)
{
int num=p;
while(result[num]<result[num-i]&&num>0)
{
temp=result[num];
result[num]=result[num-i];
result[num-i]=temp;
num-=i;
}
}
}
}
}
}
快速排序
排序过程：
对于一个数组，首先确定一个基准元素，下面的操作是最终使得基准元素左边全部小于基准元素，基准元素右边全部大于基准元素，一般数组中的第一个元素就是基准元素，给一个指针left，末尾元素给一个指针right，看right指针指向的元素是否小于基准元素，如果小于的话互换两个元素位置，并且left往后移动，如果不小于的话，right往前移动，这里是2<8，则互换两个指针位置，并且left往后移动，移动到直到找到某一个元素大于8，这里是12>8，互换两个指针位置，并且右指针往前移动，直到找到某个元素小于8，找到7小于8，互换两个指针位置.........,如此下去直到left与right指向同一个位置即基准元素位置，则完车了基准元素两边的元素分布。接下来还要对基准元素两边的子数组进行同样的操作，所以要进行递归操作。
{2、5、1、6、7、3、4} 8 {11、9、13、12、10}
{1} 2 {5、6、7、3、4} 8 {10、9} 11 {12、13}
。。。
。。
。
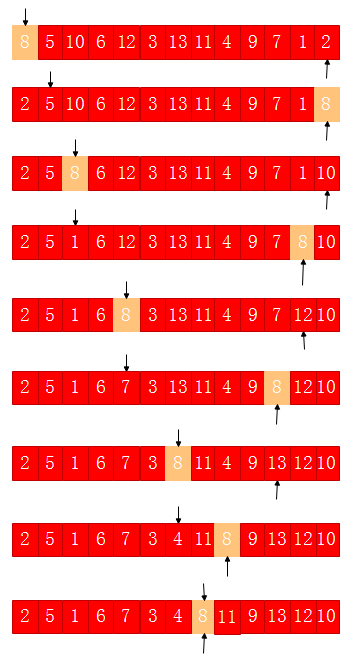
代码：
//@https://blog.51cto.com/13733462/2113397
/*快速排序*/
class solution
{
public:
vector<int> FastSort(vector<int> data,int begin,int last)
{
if(!data.empty())
return Sort(data,begin,last);
return NULL;
}
public:
vector<int> Sort(vector<int> data,int leftIndex,int rightIndex)
{
int right=rightIndex;
int left=leftIndex;
int temp=0;
while(left!=right)
{
/*如果左边数据大于右边数据，则交换位置*/
if(data[left]>data[right])
{
temp=data[left];
data[left]=data[right];
data[right]=temp;
left++;
while(data[left]<data[right])
{
left++;
if(data[left]>data[right])
{
temp=data[left];
data[left]=data[right];
data[right]=temp;
break;
}
}
}
else
{
right--;
while(data[left]<data[right])
{
right--;
if(data[left]>data[right])
{
temp=data[left];
data[left]=data[right];
data[right]=temp;
break;
}
}
}
}
Sort(data,leftIndex,left-1);
Sort(data,left+1,rightIndex);
return data;
}
}简单选择排序
排序过程：
从第一个元素开始，往后一个一个确定该位置上的元素值，刚开始第一个假设元素为最小值，与后面所有元素相比，取最小值，确定好第一个元素，再确定第二个元素，假设第二个元素是最小值，并将其与后面所有元素相比，取最小值.....后面一样的方法，直到确定所有位置上的元素为止。
动态流程图：
代码：
/*简单选择排序*/
class solution
{
public:
vector<int> SelectSort(vector<int> data)
{
vector<int> result;
result=data;
if(!data.empty())
{
sort(result);
return result;
}
return NULL;
}
void sort(vector<int> &data)
{
int minmum=0;
for(int i=0;i<data.length();i++)
{
minmum=data[i];
for(int j=i+1;j<data.length();j++)
{
if(data[j]<minmum)
{
minmum=data[j];
}
}
data[i]=minmum;
}
}
}堆排序
排序过程：
对于堆排序首先要了解的是堆排序是利用堆的性质进行排序的一种算法，这里要了解两种堆结构，大顶堆与小顶堆，每个节点的左右子节点值都大于节点值称作大顶堆，而每个节点的左右子节点的值都小于节点值称作小顶堆。下面使用的是大顶堆，对一个数组{8、7、9、5、20、13、14}按照从上到下，从左往右设置为二叉树的值，然后构造大顶堆，构造过程中，每互换两个节点的时候，要同时保证互换后，这两个节点与它们的子节点、父节点都要满足大顶堆的规则，流程如下：
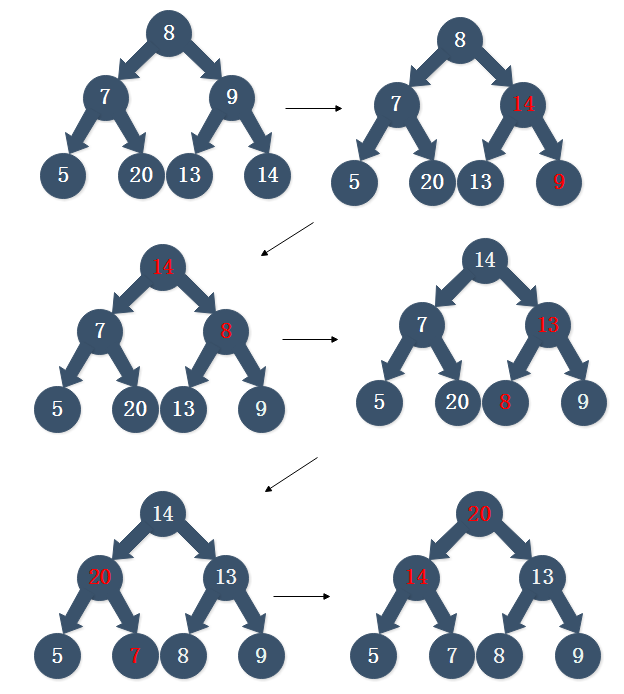
构造成一个大顶堆之后将堆顶元素与末尾元素互换位置，如下图所示，这时候末尾元素确定为我们要排序的最大值，下面要对除了该元素之外所有元素重新进行构造大顶堆，构造完了后同样将堆顶元素与末尾元素互换位置，如此下去，直到确定最后一个元素，最后就能完成整个排序。
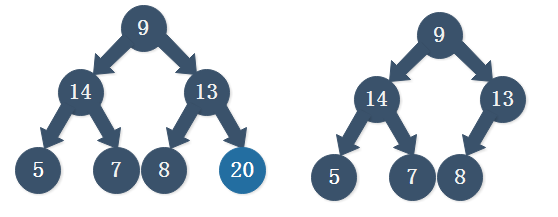
代码：
/*堆排序*/
class solution
{
public:
vector<int> HeapSort(vector<int> data)
{
vector<int> result;
result=data;
if(!data.empty())
{
Sort(result,result.begin(),result.end());
return result;
}
return NULL;
}
/*begin-end表达为数组中的元素个数*/
void Sort(vector<int> &data,int begin,int last)
{
if(last==begin)
return;
vector<int> result;
//result.push_back(data[]);
int temp=0;
for(int i=1;i<last-begin;i++)
{
/*左节点*/
if(i%2!=0)
{
if(data[i]>data[(i-1)/2])
{
temp=data[i];
data[i]=data[(i-1)/2];
data[(i-1)/2]=temp;
if(i>=3)
{
int m=(i-1)/2;
if(m%2!=0)
{
if(data[m]>data[(m-1)/2])
{
temp=data[m];
data[m]=data[(m-1)/2];
data[(m-1)/2]=temp;
}
}
else
{
if(data[m]>data[(m-2)/2])
{
temp=data[m];
data[m]=data[(m-2)/2];
data[(m-2)/2]=temp;
}
}
}
}
}
else//右节点
{
if(data[i]>data[(i-2)/2])
{
temp=data[i];
data[i]=data[(i-2)/2];
data[(i-2)/2]=temp;
if(i>=4)
{
int m=(i-2)/2;
if(m%2!=0)
{
if(data[m]>data[(m-1)/2])
{
temp=data[m];
data[m]=data[(m-1)/2];
data[(m-1)/2]=temp;
}
}
else
{
if(data[m]>data[(m-2)/2])
{
temp=data[m];
data[m]=data[(m-2)/2];
data[(m-2)/2]=temp;
}
}
}
}
}
}
if(last-begin==2)
return;
int length=last-begin-1;
/*互换第一个节点与最后一个节点位置*/
int temp=data[length];
data[length]=data[0];
data[0]=temp;
//int start=0;
int end=length;
Sort(data,0,end-1);
}
}归并排序
排序过程：
排序过程如下图所示：将所有元素分成两部分，子数组一样分成两部分，直到不能分为止，然后将两个子数组进行排序，从最小的两个数组开始排序，排序的数组越来越大，并且可以看出每次要排序的两个子数组都是升序的，已经排序好的两个子数组排序合并成一个数组如下下图所示。
动态流程图：
代码：
/*归并排序*/
class solution
{
public:
vector<int> MergeSort(vector<int> data)
{
vector<int> result;
result=data;
if(!data.empty())
{
Sort(result,result.begin(),result.end());
return result;
}
return NULL;
}
void Sort(vector<int> &data,int begin,int end)
{
if(begin==end)
return;
int left=begin;
int right=end;
int mid=(left+right)/2;
Sort(data,begin,mid);
Sort(data,mid+1,end);
int LeftIndex=mid,RightIndex=end,tempIndex=end;
int tempdata[end-begin+1];
while(LeftIndex>=begin&&RightIndex>=mid+1)
{
if(data[LeftIndex]>data[RightIndex])
{
tempdata[tempIndex]=data[LeftIndex];
tempIndex--;
LeftIndex--;
}
else
{
tempdata[tempIndex]=data[RightIndex];
tempIndex--;
RightIndex--;
}
}
while(LeftIndex>=begin)
{
tempdata[tempIndex]=data[LeftIndex];
tempIndex--;
LeftIndex--;
}
while(RightIndex>=mid+1)
{
tempdata[tempIndex]=data[RightIndex];
tempIndex--;
RightIndex--;
}
for(int i=begin;i<=end;i++)
{
data[i]=tempdata[tempIndex];
}
}
}
基数排序
排序过程：
基数排序是按照数据上的个位，十位，百位等等数据位上十位一种规则进行排序的，具体规则是，先取每个数的的个位数字，按照遍历的顺序从0~9的顺序放置，然后再按排好的顺序的基础上，再取每个数的十位数字，按照遍历顺序从0~9的顺序放置，接下来如果有百位、千位等等一样的步骤。下图是基数排序举例：
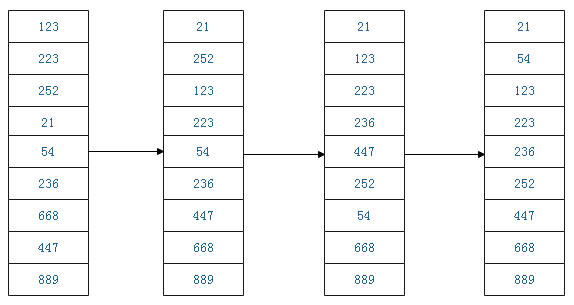
动态流程图：
代码：
/*基数排序*/
class solution
{
public:
vector<int> BaseSort(vector<int> data)
{
vector<int> result;
result=data;
if(!result.empty())
{
return Sort(result);
}
return NULL;
}
void Sort(vector<int> &data)
{
int maxmum=data[0];
for(int i=1;i<data.length();i++)
{
if(data[i]>maxmum)
maxmum=data[i];
}
int maxBit=1;
int maxBitNum=0;
while(maxmum/maxBit!=0)
{
maxBitNum++;
maxBit*=10;
}
int hash[10];
int mm=1;
int k=0;
vector<int> temp;
/*根据最大数的总位数进行从个位、十位、百位、等等往前遍历*/
for(int i=0;i<maxBitNum;i++)
{
/*哈希表初始化*/
for(int i=0;i<10;i++)
{
hash[i]=0;
}
/*哈希表计数*/
for(int i=0;i<n;i++)
{
k=(data[i]/mm)%10;
hash[k]++;
}
/*确定某一位上0~9数字的位置*/
for(int i=1;i<10;i++)
{
hash[i]=hash[i-1]+hash[i];
}
/*根据对应位上的数字放置在数组中对应的位置上*/
for(int i=0;i<n;i++)
{
k=(data[i]/mm)%10;
/*根据该位上的数字放在对应的位置上*/
temp[hash[k]-hash[k-1]]=data[i];
hash[k]--;
}
for(int i=0;i<n;i++)
{
data[i]=temp[i];
}
mm*=10;
}
}
}
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
