数据结构之二叉树（类模板实现）（C++）

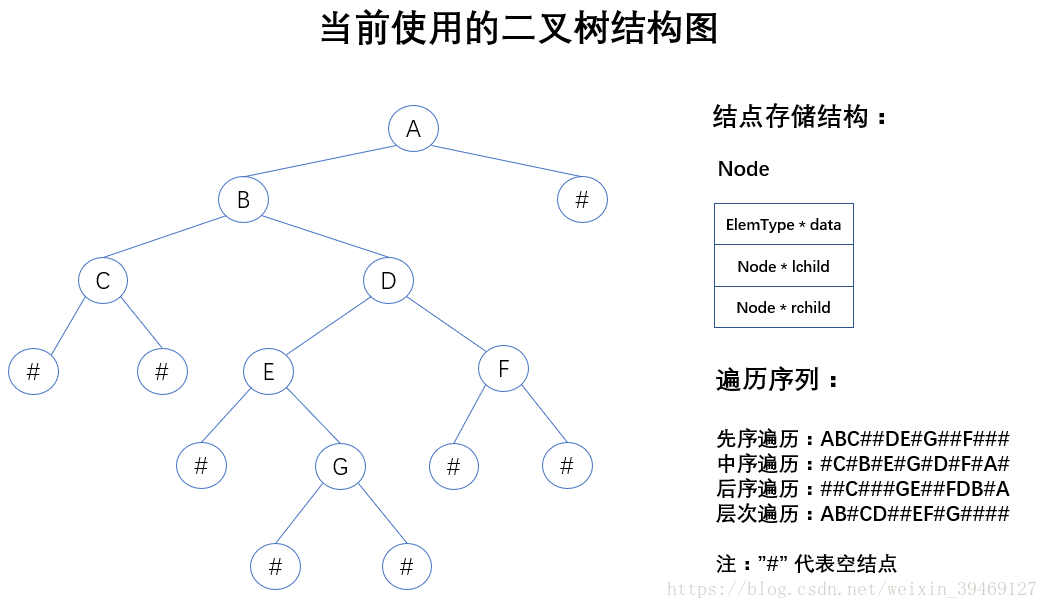
注：代码中使用的“ObjArrayList.h”、"SqStack.h"、"CQueue.h" 头文件代码在上三篇博文中已给出，分别为数据结构之顺序列表、栈、队列。

//文件名："BiTree.h"
#pragma once
#ifndef BITREE_H_
#define BITREE_H_
#include <string>
#include "ObjArrayList.h"	//顺序表（对象元素）
#include "SqStack.h"		//顺序栈（对象元素），也可用链栈
#include "CQueue.h"			//循环队列（对象元素），也可用链队列
using namespace std;

/*
.	二叉树 类模板实现 BiTree （Binary Tree）
.	存储结构：二叉链表
.	遍历方式：先序遍历（Preoder Traversal）、中序遍历（InOrder Traversal）、后序遍历（PostOrder Traversal）
.	注：元素对象需实现 输出操作符 的重载，否则无法打印树结点！
*/

//二叉树结点类型
template <typename ElemType>
struct Node
{
	ElemType * data;			//数据域
	int seq;					//完全二叉树序号
	int level;					//层次
	int num;					//层次上的坐标序号（考虑空结点）
	Node<ElemType> * lchild;	//左子树指针域
	Node<ElemType> * rchild;	//右子树指针域
};

//非递归后序遍历结点类型（含标志位）
template <typename ElemType>
struct NodeTag
{
	Node<ElemType> *p;		//二叉树结点域
	int tag;				//结点访问次数标志域：1|访问一次  2|访问二次  -1|可销毁
};

template <typename ElemType>
class BiTree
{
private:
	Node<ElemType> *bt;		//树根指针
	/*
	.	注：深度高度值虽相同，但算法上有不同
	.		1.高度：自下而上求解
	.		2.深度：自上而下求解
	*/
	int height;				//二叉树高度（自下而上定义）
	int depth;				//二叉树深度（自上而下定义）

	Node<ElemType> * _PreOrderCreate_R(ObjArrayList<ElemType> *list, int &index, int seq);	//先序遍历递归构造树（对象型结点）
	void _PostOrderDestory_R(Node<ElemType> *p);			//后序遍历递归 销毁二叉树
	
	void _CreateCoordinate(Node<ElemType> *p, int seq);		//创建结点坐标
	int _PostOrderHelght_R(Node<ElemType> *p);								//后序遍历递归 求二叉树高度（自下而上求解）
	void _PostOrderDepth_R(Node<ElemType> *p, int level, int &depth);		//后序遍历递归 求二叉树深度（自上而下求解）
	
	int _PostOrderNodeCount_R(Node<ElemType> *p);			//后序遍历递归 求结点个数
	int _PostOrderLeafCount_R(Node<ElemType> *p);			//后序遍历递归 求叶子结点个数

	bool _PreOrderCompare_R(Node<ElemType> *p, Node<ElemType> *q);	//比较二叉树是否相同
	Node<ElemType> * _PreOrderCopy_R(Node<ElemType> *p);		//复制二叉树

	void _PreOrderDisplay_R(Node<ElemType> *p);				//先序遍历递归 解析二叉树
	void _InOrderDisplay_R(Node<ElemType> *p);				//中序遍历递归 解析二叉树
	void _PostOrderDisplay_R(Node<ElemType> *p);			//后序遍历递归 解析二叉树

public:
	BiTree() { this->bt = NULL; this->height = 0; this->depth = 0; };
	BiTree(ObjArrayList<ElemType> *list);	//有参构造
	~BiTree();					//析构函数：销毁二叉树

	int Helght();				//获取二叉树高度
	int Depth();				//获取二叉树深度

	int NodeCount();			//获取二叉树结点个数
	int LeafCount();			//获取二叉树叶子结点个数

	bool Compare(BiTree<ElemType> *t);		//比较二叉树是否相同
	BiTree<ElemType> *Copy();			//复制二叉树对象

	void PreOrderDisplay_R();	//先序遍历递归 解析二叉树
	void PreOrderDisplay();		//先序遍历非递归 解析二叉树

	void InOrderDisplay_R();	//中序遍历递归 解析二叉树
	void InOrderDisplay();		//中序遍历非递归 解析二叉树

	void PostOrderDisplay_R();	//后序遍历递归 解析二叉树
	void PostOrderDisplay();	//后序遍历非递归 解析二叉树

	void LevelOrderDisplay();			//层次遍历非递归 解析二叉树
	void LevelOrderDisplayStruct();		//层次遍历非递归 打印二叉树结构
};



template <typename ElemType>
BiTree<ElemType>::BiTree(ObjArrayList<ElemType> *list)
{
	//默认采用先序遍历顺序表构造二叉树
	int index = 0;
	int seq = 1;
	this->bt = _PreOrderCreate_R(list, index, seq);
	//利用后序遍历，从下而上求树高
	this->height = _PostOrderHelght_R(this->bt);
	//利用后序遍历，从上而下求树深
	int level = 1, depth = 0;
	_PostOrderDepth_R(this->bt, level, depth);
	this->depth = depth;
}

template <typename ElemType>
BiTree<ElemType>::~BiTree()
{
	/*
	.	销毁二叉树
	*/
	_PostOrderDestory_R(this->bt);
	cout << "二叉树已销毁！" << endl;
}

template <typename ElemType>
int BiTree<ElemType>::Helght()
{
	/*
	.	获取二叉树高度
	*/
	return this->height;
}

template <typename ElemType>
int BiTree<ElemType>::Depth()
{
	/*
	.	获取二叉树高度
	*/

	return this->depth;
}

template <typename ElemType>
int BiTree<ElemType>::NodeCount()
{
	/*
	.	获取二叉树结点个数
	*/
	return _PostOrderNodeCount_R(this->bt);
}

template <typename ElemType>
int BiTree<ElemType>::LeafCount()
{
	/*
	.	获取二叉树叶子结点个数
	*/
	return _PostOrderLeafCount_R(this->bt);
}

template <typename ElemType>
bool BiTree<ElemType>::Compare(BiTree<ElemType> *t)
{
	/*
	.	比较两棵树是否相同
	*/
	return _PreOrderCompare_R(this->bt, t->bt);
}

template <typename ElemType>
BiTree<ElemType> *BiTree<ElemType>::Copy()
{
	/*
	.	比较两棵树是否相同
	*/
	//初始化二叉树对象
	BiTree<ElemType> *t = new BiTree<ElemType>();
	//复制二叉树（对象数据，非对象地址）
	t->bt = _PreOrderCopy_R(this->bt);
	t->height = this->height;
	t->depth = this->depth;
	return t;
}

template <typename ElemType>
Node<ElemType> *BiTree<ElemType>::_PreOrderCreate_R(ObjArrayList<ElemType> *list, int &index, int seq)
{
	/*
	.	先序遍历递归创建二叉树
	.	入参：
	.		ObjArrayList<ElemType> *list : 先序遍历组合的对象结点顺序表
	.		int &index: 顺序表遍历索引
	.		int seq: 以完全二叉树，对每个结点排序
	.	出参：
	.		Node<ElemType> * : 树根结点指针
	.	注：以顺序表（对象元素结点）创建
	*/
	Node<ElemType> *p = NULL;
	//1.超出顺序表时返回，结束
	if (index >= list->Length())
	{
		return p;
	}
	//2.元素为 NULL 时，意为空结点
	else if (list->Get(index) == NULL)
	{
		return p;
	}
	//3.创建根结点，并递归创建其左右子树
	else
	{
		p = new Node<ElemType>;
		p->data = list->Get(index);
		_CreateCoordinate(p, seq);	//创建结点坐标
		p->lchild = _PreOrderCreate_R(list, ++index, 2 * seq);
		p->rchild = _PreOrderCreate_R(list, ++index, 2 * seq + 1);
	}
	return p;
}

template <typename ElemType>
void BiTree<ElemType>::_PostOrderDestory_R(Node<ElemType> *p)
{
	/*
	.	后序遍历 递归 销毁二叉树
	.	注：需先销毁子节点，再根结点
	*/
	if (p != NULL)
	{
		_PostOrderDestory_R(p->lchild);
		_PostOrderDestory_R(p->rchild);
		delete p;
	}
}

template <typename ElemType>
void BiTree<ElemType>::_CreateCoordinate(Node<ElemType> *p, int seq)
{
	/*
	.	创建结点坐标
	.	入参：
	.		Node<ElemType> *p: 树结点
	.		int seq: 完全二叉树的形式的结点序号
	*/
	p->seq = seq;	//结点序号（完全二叉树形式）
	p->level = (int)floor(log(seq) / log(2)) + 1;	//结点所在层次深度：floor( log2(seq) ) + 1；log2() 利用换底公式：log2(x) = log(x)/log(2)
	p->num = seq - (int)pow(2, p->level - 1) + 1;	//结点所在层次的结点位置序号：seq - 上层末尾结点序号（完全二叉树形式）
}

template <typename ElemType>
int BiTree<ElemType>::_PostOrderHelght_R(Node<ElemType> *p)
{
	/*
	.	后序遍历 递归求二叉树高度（自下而上）
	.	入参：
	.		1.Node<ElemType> *p: 树结点
	.	出参：
	.		1.int : 子树高度
	.	算法解析：
	.		1.求每颗子树的高度（左右子树高度取最大）
	.		2.叶子结点高度为 1
	*/
	int lheight = 0, rheight = 0;
	if (p != NULL)
	{
		lheight = _PostOrderHelght_R(p->lchild);
		rheight = _PostOrderHelght_R(p->rchild);
		return (lheight > rheight ? lheight : rheight) + 1;	//返回较大的一个树深 + 1 (根结点)
	}
	return 0;	//空结点返回 0
}

template <typename ElemType>
void BiTree<ElemType>::_PostOrderDepth_R(Node<ElemType> *p, int level, int &depth)
{
	/*
	.	后序遍历递归 求树深度（自上而下）
	.	入参：
	.		1.Node<ElemType> *p: 树结点
	.		2.int level: 树层次
	.		3.int &depth: 树深度
	.	算法解析：
	.		1.depth = max[ level(i) ]	, 其中i 为每一个根到叶的路径
	.		2.自上而下体现在：level 的逐层往下增加
	*/
	if (p != NULL)
	{
		_PostOrderDepth_R(p->lchild, level + 1, depth);
		_PostOrderDepth_R(p->rchild, level + 1, depth);
		//若为叶子节点，则一条根叶路径走完，比较深度
		//if (p->lchild == NULL && p->rchild == NULL)	//此判断多此一举，上层深度不可能比下层大
			if (level > depth)
				depth = level;
	}
}

template <typename ElemType>
int BiTree<ElemType>::_PostOrderNodeCount_R(Node<ElemType> *p)
{
	/*
	.	后序遍历递归 求树结点数
	*/
	if (p != NULL)
		return _PostOrderNodeCount_R(p->lchild) + _PostOrderNodeCount_R(p->rchild) + 1; //先左，后右，再返回相加结果，即为后序
	return 0;
}

template <typename ElemType>
int BiTree<ElemType>::_PostOrderLeafCount_R(Node<ElemType> *p)
{
	/*
	.	后序遍历递归 求树叶子结点数
	*/
	if (p != NULL)
	{
		if (p->lchild == NULL && p->rchild == NULL)
			return 1;
		else
			return _PostOrderLeafCount_R(p->lchild) + _PostOrderLeafCount_R(p->rchild); //先左，后右，再返回相加结果，即为后序
	}
	return 0;
}
template <typename ElemType>
bool BiTree<ElemType>::_PreOrderCompare_R(Node<ElemType> *p, Node<ElemType> *q)
{
	/*
	.	先序遍历递归 比较两颗二叉树是否相同
	*/
	if (p != NULL && q != NULL)
	{
		//先比较根结点元素（结点元素类需实现 Compare() 接口），后比较左右子树
		return (p->data->Compare(q->data))
			&& _PreOrderCompare_R(p->lchild, q->lchild) 
			&& _PreOrderCompare_R(p->rchild, q->rchild);
	}
	else if (p == NULL && q == NULL)
		return true;
	else
		return false;
}

template <typename ElemType>
Node<ElemType> * BiTree<ElemType>::_PreOrderCopy_R(Node<ElemType> *p)
{
	/*
	.	先序遍历递归 复制二叉树（实现复制对象数据，并非对象地址！！）
	*/
	Node<ElemType> *q = NULL;
	if (p != NULL)
	{
		q = new Node<ElemType>;
		q->data = p->data->Copy();	//结点元素类需实现 Copy() 接口！！
		q->lchild = _PreOrderCopy_R(p->lchild);
		q->rchild = _PreOrderCopy_R(p->rchild);
	}
	return q;
}

template <typename ElemType>
void BiTree<ElemType>::PreOrderDisplay_R()
{
	/*
	.	先序遍历递归显示二叉树
	*/
	cout << "The BiTree is: ";
	_PreOrderDisplay_R(this->bt);
	cout << endl;
}

template <typename ElemType>
void BiTree<ElemType>::_PreOrderDisplay_R(Node<ElemType> *p)
{
	/*
	.	先序遍历递归显示二叉树
	*/
	if (p != NULL)
	{
		cout << p->data << " ";
		_PreOrderDisplay_R(p->lchild);
		_PreOrderDisplay_R(p->rchild);
	}
	else
	{
		cout << "# ";	//空结点以 '#' 代替
	}
}

template <typename ElemType>
void BiTree<ElemType>::PreOrderDisplay()
{
	/*
	.	先序遍历 非递归 解析二叉树
	.	算法：（栈）
	.		1.先访问子树根结点，根结点入栈，然后访问左子树；
	.		2.等到子树根结点为空，出栈根结点，访问其右子树；
	.		3.如此循环...
	*/
	//树根结点
	Node<ElemType> *p = this->bt;
	//初始化栈，存放压栈结点
	SqStack<Node<ElemType>> *st = new SqStack<Node<ElemType>>(20);	//栈容量 需满足 二叉树深度减一
	/*	按照一般思路写出的代码，其中两个 while 可以合并，如下结果
	//子树根结点不为空，遍历整棵树
	while (p != NULL)
	{
		//1.输出子树根结点
		cout << p->data << " ";
		//2.入栈根结点（含NULL）（也可入栈右子树结点，但这样就不可输出 NULL 结点）
		st->Push(p);
		//3.指针 p 移到左子树结点
		p = p->lchild;
		//输出 左子树（NULL）结点
		if (p == NULL)
			cout << "# ";
		//4.若子树结点为空，且栈不为空
		while (p == NULL && !st->Empty())
		{
			//则出栈，且指针 p 移到出栈结点右子树上
			p = st->Pop();
			p = p->rchild;
			//输出 右子树（NULL）结点
			if (p == NULL)
				cout << "# ";
		}
	}
	*/
	cout << "The BiTree is: ";
	//子树根结点不为空，且栈不为空，遍历整棵树
	while (p != NULL || !st->Empty())
	{
		//1.子树根结点不为空
		if (p != NULL)
		{
			//1.输出子树根结点
			cout << p->data << " ";
			//2.入栈根结点（含NULL）（也可入栈右子树结点，但这样就不可输出 NULL 结点）
			st->Push(p);
			//3.指针 p 移到左子树结点
			p = p->lchild;			
		}
		//2.子树结点为空
		else
		{
			//则出栈，且指针 p 移到出栈结点右子树根上
			p = st->Pop();
			p = p->rchild;
		}
		//输出 子树（NULL）结点（左右）
		if (p == NULL)
			cout << "# ";
	}
	cout << endl;
	//释放栈
	delete st;
}

template <typename ElemType>
void BiTree<ElemType>::InOrderDisplay_R()
{
	/*
	.	中序遍历递归显示二叉树
	*/
	cout << "The BiTree is: ";
	_InOrderDisplay_R(this->bt);
	cout << endl;
}

template <typename ElemType>
void BiTree<ElemType>::_InOrderDisplay_R(Node<ElemType> *p)
{
	/*
	.	中序遍历递归显示二叉树
	*/
	if (p != NULL)
	{
		_InOrderDisplay_R(p->lchild);
		cout << p->data << " ";
		_InOrderDisplay_R(p->rchild);
	}
	else
	{
		cout << "# ";	//空结点以 '#' 代替
	}
}

template <typename ElemType>
void BiTree<ElemType>::InOrderDisplay()
{
	/*
	.	中序遍历 非递归 显示二叉树
	.	算法：（栈）
	.		1.先根结点入栈，然后访问左子树；
	.		2.等到子树根结点为空，出栈根结点，访问根结点，访问右子树；
	.		3.如此循环...
	*/
	//初始化根结点
	Node<ElemType> *p = this->bt;
	//初始化栈，存放压栈结点
	SqStack<Node<ElemType>> *st = new SqStack<Node<ElemType>>(20);	//栈容量 需满足 二叉树深度减一
	cout << "The BiTree is: ";
	//子树根结点不为空，且栈不为空，遍历整棵树
	while (p != NULL || !st->Empty())
	{
		//1.子树根结点不为空
		if (p != NULL)
		{
			//1.入栈根结点（含NULL）（也可入栈右子树结点，但这样就不可输出 NULL 结点）
			st->Push(p);
			//2.指针 p 移到左子树结点
			p = p->lchild;
		}
		//2.子树结点为空
		else
		{
			//1.则出栈
			p = st->Pop();
			//2.输出子树根结点
			cout << p->data << " ";
			//3.指针 p 移到出栈结点右子树根上
			p = p->rchild;
		}
		//输出 子树（NULL）结点（左右）
		if (p == NULL)
			cout << "# ";
	}
	cout << endl;
	//释放栈
	delete st;
}

template <typename ElemType>
void BiTree<ElemType>::PostOrderDisplay_R()
{
	/*
	.	后序遍历递归显示二叉树
	*/
	cout << "The BiTree is: ";
	_PostOrderDisplay_R(this->bt);
	cout << endl;
}

template <typename ElemType>
void BiTree<ElemType>::_PostOrderDisplay_R(Node<ElemType> *p)
{
	/*
	.	后序遍历递归显示二叉树
	*/
	if (p != NULL)
	{
		_PostOrderDisplay_R(p->lchild);
		_PostOrderDisplay_R(p->rchild);
		cout << p->data << " ";
	}
	else
	{
		cout << "# ";	//空结点以 '#' 代替
	}
}

template <typename ElemType>
void BiTree<ElemType>::PostOrderDisplay()
{
	/*
	.	后序遍历 非递归 显示二叉树
	.	算法：（栈）
	.		1.先入栈子树根结点（访问次数默认1），访问左子树结点；
	.		2.直到子树根结点为空，出栈根结点：
	.			2.1.若其访问次数为1，则标记其为2，并将其再入栈，访问其右子树；
	.			2.2.若其访问次数为2，则访问根结点；
	.		3.如此循环...
	.		注：也可每次入栈根结点、右子树结点，这样会比只入栈根结点多一倍的栈容量，但可不用区分栈中根结点第几次被访问
	*/
	//初始化根结点
	Node<ElemType> *p = this->bt;
	//初始化带标识位结点
	NodeTag<ElemType> *nt = NULL;
	//初始化栈，存放压栈结点
	SqStack<NodeTag<ElemType>> *st = new SqStack<NodeTag<ElemType>>(20);	//栈容量 需满足 二叉树深度减一
	cout << "The BiTree is: ";
	//子树根结点不为空，且栈不为空，遍历整棵树
	while (p != NULL || !st->Empty())
	{
		//1.子树根结点不为空
		if (p != NULL)
		{
			//0.创建带标识位的结点
			nt = new NodeTag<ElemType>;
			nt->p = p;		//赋值根结点
			nt->tag = 1;	//标识位初始默认 1
			//1.入栈根结点（带标识位）
			st->Push(nt);
			//2.指针 p 移到左子树根结点
			p = p->lchild;
		}
		//2.子树根结点为空
		else
		{
			//1.出栈根结点
			nt = st->Pop();
			//2.若第一次访问
			if (nt->tag == 1)
			{
				//1.置标识位 2 ，根结点再次入栈
				nt->tag = 2;
				st->Push(nt);
				//2.指针 p 移到右子树根结点
				p = nt->p->rchild;
			}
			//3.若第二次访问
			else
			{
				//输出根结点
				cout << nt->p->data << " ";
				//标记结点为可销毁 -1 状态
				nt->tag = -1;
			}
		}
		//输出 子树（NULL）结点（左右），且出栈根结点为可销毁（-1）状态
		if (p == NULL && nt->tag != -1)
			cout << "# ";
		//销毁 nt 指向的标志结点内存
		if (nt->tag == -1)
			delete nt;
		//置空 nt
		nt = NULL;	//置空
	}
	cout << endl;
	delete st;
}

template <typename ElemType>
void BiTree<ElemType>::LevelOrderDisplay()
{
	/*
	.	层次遍历 非递归 显示二叉树
	.	算法：（队列）
	.		1.将树根结点入队；
	.		2.出队结点，访问子树根结点，为空时输出"#",非空时输出结点，入队左、右子树；
	.		3.如此循环 2 ...
	.		注：两种结点访问时机：
	.			1.结点入队前：需分左右子树输出，代码不统一。
	.			2.结点出队后：统一由出队子树根结点输出，代码更统一。（此处采用）
	*/
	//初始化队列
	CQueue<Node<ElemType>> *cq = new CQueue<Node<ElemType>>(20);	//入队容量 需满足 结点数最多的一层（ <= 取最深层叶子节点数 (2^n - 1) ）
	//初始化结点指针
	Node<ElemType> *p = NULL;

	cout << "The BiTree is: ";
	if (this->bt == NULL)
		return;
	//1.入队根结点
	cq->EnQueue(this->bt);
	//2.循环出队，访问子树
	while (!cq->isEmpty())
	{	
		//1.出队 子树根结点
		p = cq->DeQueue();
		//1.1.为空：输出 "#"
		if (p == NULL)
			cout << "# ";
		//1.2.非空：访问子树
		else
		{
			//1.访问根结点
			cout << p->data << " ";
			//2.入队 左子树
			cq->EnQueue(p->lchild);
			//3.入队 右子树
			cq->EnQueue(p->rchild);
		}
	}
	cout << endl;
	delete cq;
}

template <typename ElemType>
void BiTree<ElemType>::LevelOrderDisplayStruct()
{
	/*
	.	层次遍历 非递归 打印二叉树结构（含结点坐标信息）
	.	结点坐标信息：
	.		1.seq		: 完全二叉树序号
	.		2.level		: 层次
	.		3.num		: 层次上的坐标序号（考虑空结点）
	.	算法：（队列）
	.		1.访问根结点，将其入队；
	.		2.出队结点，先访问左子树（非空时输出、入队，空时输出 "#"），后访问右子树（非空时输出、入队，空时输出 "#"）；
	.		3.如此循环 2 ...
	.		注：两种结点访问时机：
	.			1.结点入队前：需分左右子树输出，代码不统一，但是可以由出队结点确定其下子树 NUlL 的层次。（此处采用）
	.			2.结点出队后：统一由出队子树根结点输出，代码更统一。
	.
	.	注：目前还是实现不了结点位置的准确输出---！！！
	.	（想法：再实现一个坐标类，可将结点坐标输进去，就能显示了）
	*/
	//初始化队列
	CQueue<Node<ElemType>> *cq = new CQueue<Node<ElemType>>(20);	//入队容量 需满足 结点数最多的一层（ <= 取最深层叶子节点数 (2^n - 1) ）
	//初始化结点指针
	Node<ElemType> *p = NULL, *q = NULL;
	//初始化树层次
	int level = 1;
	//初始化标记
	int tag = -1;	// -1|队列出队  0|访问右子树  1|访问左子树

	cout << "The BiTree Struct is: " << endl;
	if (this->bt == NULL)
		return;
	//1.访问根结点，将其入队
	cout << this->bt->data << " ";
	cq->EnQueue(this->bt);
	//2.循环出队，访问子树
	while (!cq->isEmpty() || tag != -1)
	{
		//标记：出队
		if (tag == -1)
		{
			//1.出队 子树根结点
			p = cq->DeQueue();
			//如果 p->level + 1 > level ，则转为下一层
			if (p->level + 1 > level)
			{
				level = p->level + 1;	//出队元素层次 + 1，即为当前层次
				cout << endl;
			}
			tag = 0;	//将标记置为 0
			continue;	//进入下一次循环
		}
		//标记：访问左子树
		else if (tag == 0)
		{
			q = p->lchild;
			tag = 1;	//将标记置为 1
		}
		//标记：访问右子树
		else
		{
			q = p->rchild;
			tag = -1;	//将标记置为 -1
		}
		
		//访问子树结点
		if (q == NULL)
			cout << "# ";
		else
		{
			//1.1.访问子树结点
			cout << q->data << "_(" << q->seq << "," << q->level << "," << q->num << ") ";
			//1.2.入队 子树
			cq->EnQueue(q);
		}
	}
	cout << endl;
	delete cq;
}

#endif // !BITREE_H_

//文件名："BiTree_Test.cpp"
#include "stdafx.h"
#include <iostream>
#include "BiTree.h"
#include "ObjArrayList.h"
using namespace std;

//树结点元素
struct Element
{
	char a;
	int b;
public:
	bool Compare(Element *p)
	{
		/*
		.	实现元素对象比较接口
		*/
		return a == p->a;
	}
	Element *Copy()
	{
		/*
		.	实现元素对象复制接口
		*/
		Element *p = new Element;
		p->a = a;
		p->b = b;
		return p;
	}
	friend ostream & operator <<(ostream& out, Element *p)
	{
		/*
		.	友元函数重载输出操作符，实现对象输出
		*/
		out << "(" << p->a << "," << p->b << ")";
		return out;
	}
};

int mian()
{
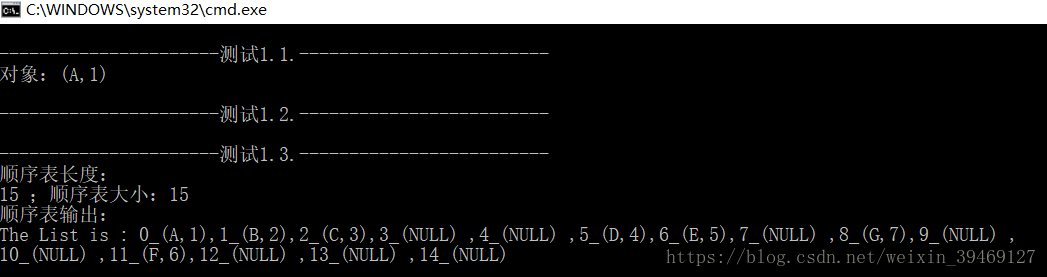
	cout << endl << "----------------------测试1.1.-------------------------" << endl;
	//1.1.测试 元素对象 输出
	Element *e = new Element{ 'A',1 };
	cout << "对象：" << e << endl;

	cout << endl << "----------------------测试1.2.-------------------------" << endl;
	//1.2.以 先序遍历的结点顺序 存放元素结点于 顺序列表 中
	//.................012345678901234
	//先序遍历字符串："ABC##DE#G##F###";	//15个字符
	ObjArrayList<Element> *list = new ObjArrayList<Element>(15);
	list->Add(0, new Element{ 'A',1 });
	list->Add(1, new Element{ 'B',2 });
	list->Add(2, new Element{ 'C',3 });
	list->Add(3, NULL);
	list->Add(4, NULL);
	list->Add(5, new Element{ 'D',4 });
	list->Add(6, new Element{ 'E',5 });
	list->Add(7, NULL);
	list->Add(8, new Element{ 'G',7 });
	list->Add(9, NULL);
	list->Add(10, NULL);
	list->Add(11, new Element{ 'F',6 });
	list->Add(12, NULL);
	list->Add(13, NULL);
	list->Add(14, NULL);

	cout << endl << "----------------------测试1.3.-------------------------" << endl;
	//1.3.测试 顺序列表 输出
	cout << "顺序表长度：" << endl << list->Length() << " ；顺序表大小：" << list->Size() << endl;
	cout << "顺序表输出：" << endl << list << endl;

	cout << endl << "----------------------测试2.1.-------------------------" << endl;
	//2.1.测试 创建二叉树（先序遍历）
	BiTree<Element> *t = new BiTree<Element>(list);

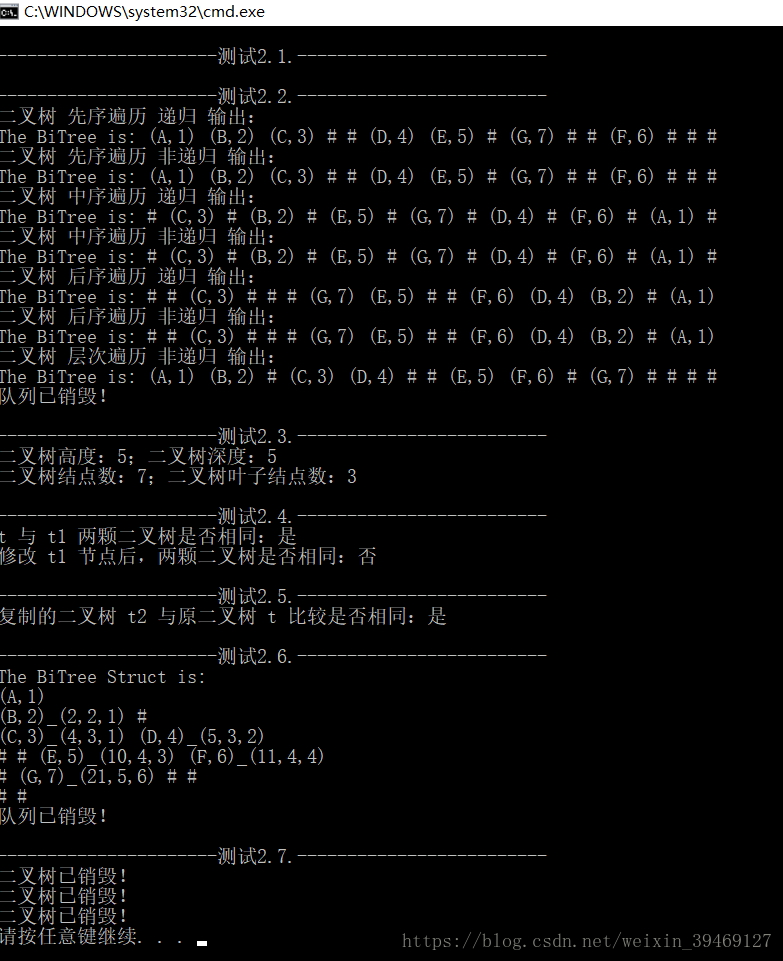
	cout << endl << "----------------------测试2.2.-------------------------" << endl;
	//2.2.测试 显示二叉树（先序、中序、后续遍历）
	cout << "二叉树 先序遍历 递归 输出：" << endl;
	t->PreOrderDisplay_R();
	cout << "二叉树 先序遍历 非递归 输出：" << endl;
	t->PreOrderDisplay();
	cout << "二叉树 中序遍历 递归 输出：" << endl;
	t->InOrderDisplay_R();
	cout << "二叉树 中序遍历 非递归 输出：" << endl;
	t->InOrderDisplay();
	cout << "二叉树 后序遍历 递归 输出：" << endl;
	t->PostOrderDisplay_R();
	cout << "二叉树 后序遍历 非递归 输出：" << endl;
	t->PostOrderDisplay();
	cout << "二叉树 层次遍历 非递归 输出：" << endl;
	t->LevelOrderDisplay();

	cout << endl << "----------------------测试2.3.-------------------------" << endl;
	//2.3.测试 树属性
	cout << "二叉树高度：" << t->Helght() << "；二叉树深度：" << t->Depth() << endl;
	cout << "二叉树结点数：" << t->NodeCount() << "；二叉树叶子结点数：" << t->LeafCount() << endl;

	cout << endl << "----------------------测试2.4.-------------------------" << endl;
	//2.4.测试 二叉树两两比较
	ObjArrayList<Element> *list1 = new ObjArrayList<Element>(15);
	list1->Add(0, new Element{ 'A',1 });
	list1->Add(1, new Element{ 'B',2 });
	list1->Add(2, new Element{ 'C',3 });
	list1->Add(3, NULL);
	list1->Add(4, NULL);
	list1->Add(5, new Element{ 'D',4 });
	list1->Add(6, new Element{ 'E',5 });
	list1->Add(7, NULL);
	list1->Add(8, new Element{ 'G',7 });
	list1->Add(9, NULL);
	list1->Add(10, NULL);
	list1->Add(11, new Element{ 'F',6 });
	list1->Add(12, NULL);
	list1->Add(13, NULL);
	list1->Add(14, NULL);
	BiTree<Element> *t1 = new BiTree<Element>(list1);
	cout << "t 与 t1 两颗二叉树是否相同：" << (t->Compare(t1) ? "是" : "否") << endl;
	//更改二叉树 t1 结点 后再比较
	list1->Get(11)->a = 'H';
	cout << "修改 t1 节点后，两颗二叉树是否相同：" << (t->Compare(t1) ? "是" : "否") << endl;

	cout << endl << "----------------------测试2.5.-------------------------" << endl;
	//2.5.测试 二叉树复制
	BiTree<Element> *t2 = t->Copy();
	cout << "复制的二叉树 t2 与原二叉树 t 比较是否相同：" << (t->Compare(t2) ? "是" : "否") << endl;

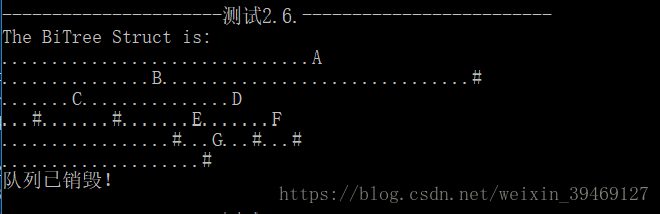
	cout << endl << "----------------------测试2.6.-------------------------" << endl;
	//2.6.测试 以二叉树结构输出
	t->LevelOrderDisplayStruct();

	cout << endl << "----------------------测试2.7.-------------------------" << endl;
	//2.7.测试 二叉树销毁
	delete t;
	delete t1;
	delete t2;
	
	return 0;
}

增加函数：int BiTree<ElemType>::_CalSpaceNum_Coordinate(int level, int num)

修改函数：void BiTree<ElemType>::LevelOrderDisplayStruct()

实现二叉树树形打印：

template <typename ElemType>
void BiTree<ElemType>::LevelOrderDisplayStruct()
{
	/*
	.	层次遍历 非递归 打印二叉树结构（含结点坐标信息）
	.	结点坐标信息：
	.		1.seq		: 完全二叉树序号
	.		2.level		: 层次
	.		3.num		: 层次上的坐标序号（考虑空结点）
	.	算法：（队列）
	.		1.访问根结点，将其入队；
	.		2.出队结点，先访问左子树（非空时输出、入队，空时输出 "#"），后访问右子树（非空时输出、入队，空时输出 "#"）；
	.		3.如此循环 2 ...
	.		注：两种结点访问时机：
	.			1.结点入队前：需分左右子树输出，代码不统一，但是可以由出队结点确定其下子树 NUlL 的层次。（此处采用）
	.			2.结点出队后：统一由出队子树根结点输出，代码更统一。
	.
	.	二叉树形打印示例图及相关公式：
	.		1.公式：
	.			1.1.计算每层第一个结点左侧空格数
	.				space_i_first = pow(2, tol_level - level) - 1;
	.			1.2.计算各层结点间的空格数（间距）
	.				space_i = 2 * space_i_first + 1;
	.			1.3.计算第 n 层 第 num 个结点前的空格数
	.				space_num = (num - 1) * (space_i + 1) + space_i_first; //其中 space_i + 1 意为 空格数加上结点本身占的位置
	.			1.4.计算当前层上当前结点前实际需要打印的空格数
	.				1.4.1.当前层上 第一次 打印结点：直接打印当前结点前空格数 cur_space_num
	.				1.4.1.当前层上 第二次及以上 打印结点：打印 当前结点空格 - 之前结点空格（需加上本身）
	.														cur_space_num - (last_space_num + 1)
	.		2.图例：
	.		(注：图中以 '.' 代表空格，因为 数个'_'连在一起，分不清个数)
	.												space_i_first			space_i
	.	1	...............A................		15 = 2^(5-1)-1			31 = 15*2+1
	.	2	.......A...............A........		7 = 2^(5-2)-1			15 = 7*2+1
	.	3	...A.......A.......A.......A....		3 = 2^(5-3)-1			7 = 3*2+1
	.	4	.A...A...A...A...A...A...A...A..		1 = 2^(5-4)-1			3 = 1*2+1
	.	5	A.A.A.A.A.A.A.A.A.A.A.A.A.A.A.A.		0 = 2^(5-5)-1			1 = 0*2+1
	.
	*/
	//初始化队列
	CQueue<Node<ElemType>> *cq = new CQueue<Node<ElemType>>(20);	//入队容量 需满足 结点数最多的一层（ <= 取最深层叶子节点数 (2^n - 1) ）
	//初始化结点指针
	Node<ElemType> *p = NULL, *q = NULL;
	//初始化树层次
	int level = 1;
	//初始化当前层上结点的序号
	int num = 1;
	//初始化当前层上的空格打印信息
	int last_space_num = 0;	//当前层的上一个结点前的空格数
	int cur_space_num = 0;	//当前层的当前结点前的空格数
	
	//初始化标记
	int tag = -1;	// -1|队列出队  0|访问右子树  1|访问左子树

	cout << "The BiTree Struct is: " << endl;
	if (this->bt == NULL)
		return;
	q = this->bt;
	//2.循环出队，访问子树
	while (q == this->bt || !cq->isEmpty() || tag != -1)
	{
		//计算当前层的当前结点前的空格数
		cur_space_num = _CalSpaceNum_Coordinate(level, num);
		/*
		.	打印空格：（两种情况）
		.		1.当前结点是本层上打印的第一个结点（序号不一定为 1 ），即：last_space_num == 0 时，直接打印空格数
		.		2.当前结点不是本层上打印的第一个结点，即：last_space_num != 0时，需减掉之前结点及空格数
		*/
		for (int i = 0; i < cur_space_num - (last_space_num == 0 ? 0 : last_space_num + 1); i++)
			cout << ".";
		//上一结点前空格数 赋值上 当前结点前空格数，并置当前结点空格数为 0
		last_space_num = cur_space_num;
		cur_space_num = 0;
		//访问子树结点
		if (q == NULL)
			cout << "#";	//空结点输出
		else
		{
			//1.访问子树结点
			cout << q->data;
			//2.入队 子树
			cq->EnQueue(q);
			q = NULL;	//指针 q 置空
		}

		//标记：出队
		if (tag == -1)
		{
			//1.出队 子树根结点
			p = cq->DeQueue();
			//如果 p->level + 1 > level ，则转为下一层
			if (p->level + 1 > level)
			{
				level = p->level + 1;	//出队元素层次 + 1，即为当前层次
				last_space_num = 0;		//置为下一层时，空格数置 0
				cout << endl;
			}
			tag = 0;	//将标记置为 0
		}

		//标记：访问左子树
		if (tag == 0)
		{
			q = p->lchild;
			if (q == NULL)
				num = 2 * p->seq - (int)pow(2, level - 1) + 1;	//根据双亲结点，计算其左子树结点层上序号（含空结点）
			else
				num = q->num;
			tag = 1;	//将标记置为 1
		}
		//标记：访问右子树
		else if (tag == 1)
		{
			q = p->rchild;
			num = num + 1;	//根据 左子树结点 + 1， 即为右子树结点层上序号（含空结点）
			tag = -1;	//将标记置为 -1
		}
	}
	cout << endl;
	delete cq;
}

template <typename ElemType>
int BiTree<ElemType>::_CalSpaceNum_Coordinate(int level, int num)
{
	/*
	.	计算结点需打印空格数（坐标计算）
	.	入参：
	.		1.int level: 当前结点所在层数
	.		2.int num: 当前层的第几个结点（含空结点，按完全二叉树形式）
	.	出参：
	.		1.int : 需打印坐标空格数
	*/
	int tol_level = this->height + 1;									//树的总层数 + 1 （希望将最后一层之下的空层也打印）
	int space_i_first = (int)pow(2, tol_level - level) - 1;				//各层首个结点前空格数
	int space_i = 2 * space_i_first + 1;								//各层结点间空格数
	int space_num = (num - 1) * (space_i + 1) + space_i_first;			//返回结点前空个数
	return space_num;
}

打印结果：