本文详细介绍了HashMap的工作原理，包括其在JDK1.8之前的数组+链表结构和JDK1.8之后引入的红黑树优化。探讨了HashMap的扩容机制、链表转红黑树的条件以及不同版本中put和get方法的实现细节。
简介
- JDK1.8之前：数组(HashMap主体) + 链表(解决Hash冲突--“拉链法”)
- JDK1.8之后：数组(HashMap主体) + 链表(解决Hash冲突--“拉链法”) + 红黑树
链表转红黑树条件：- 链表长度>8(默认值)
- HashMap数组长度>64
基本原理
扩容机制
默认长度为16，初始化时判断容量是否是2的幂次方，如果不是扩容至最接近的幂次方。
优势：
充分利用数组的每个角标位，不会造成空间的浪费，同时扩容时不需要重新hash，效率更好。
使用2的幂次方的原因：
扩容后，数据迁移时，数据要么在原来的位置，要么在原来的位置+扩容长度，不需要重新hash--效率更好。
扩容时间
JDK1.7:
- 判断是否到达阈值（0.75*数组长度[容量]）
- 同时判断是否产生hash冲突
- 扩容后，再添加元素
//元素个数大于阈值，同时当前索引位有值，就会执行扩容操作
if ((size >= threshold) && (null != table[bucketIndex])) {
//2倍扩容
resize(2 * table.length);
hash = (null != key) ? hash(key) : 0;
//重新计算索引位置
bucketIndex = indexFor(hash, table.length);
}
//基于键值创建Entry节点，并以头插法存入对应位置
createEntry(hash, key, value, bucketIndex);
JDK1.8:
- 先添加元素
- 判断是否达到阈值
插入元素
...
// 实际大小大于阈值则扩容
if (++size > threshold)
resize();
...
扩容方法
JDK1.7:
- 添加元素采用头插法
- 将单向链表的数据进行迁移
void transfer(Entry[] newTable, boolean rehash) {
int newCapacity = newTable.length; // 扩容后的长度
for (Entry<K,V> e : table) { // 遍历整个数组的索引
while(null != e) { // 判断桶中是否有元素--链表结构
//记录遍历到的元素的下一个元素
Entry<K,V> next = e.next;
if (rehash) {
e.hash = null == e.key ? 0 : hash(e.key);
}
//使用扩容后的容量计算新数组的角标位置
int i = indexFor(e.hash, newCapacity);
//把当前元素的下一个改为新数组对应位置的元素--头插法
e.next = newTable[i];
//将当前元素放置在数组对应索引位置
newTable[i] = e;
//指针向下移动
e = next;
}
}
}
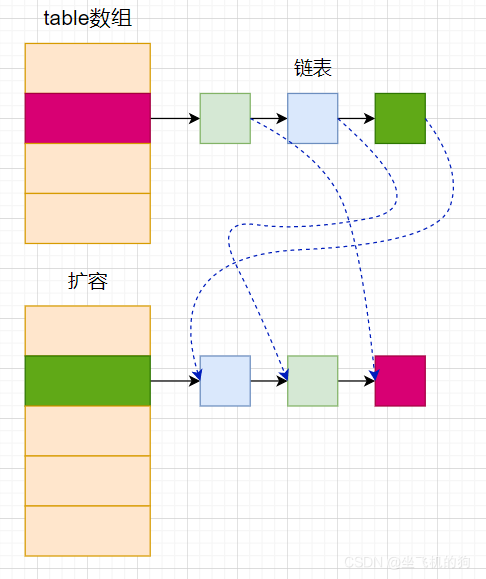
JDK1.8:
- 添加元素使用尾插法
- 如果是单向链表，将单向链表进行数据迁移
- 如果对应角标是红黑树，将双向链表(为了做数据迁移)进行数据迁移
// 在链表最末插入结点
for (int binCount = 0; ; ++binCount) {
// 到达链表的尾部
if ((e = p.next) == null) {
// 在尾部插入新结点
p.next = newNode(hash, key, value, null);
// 结点数量达到阈值(默认为 8[长度为8时hash冲突的概率已经很小了])，执行 treeifyBin 方法
// 这个方法会根据 HashMap 数组来决定是否转换为红黑树。
// 只有当数组长度大于或者等于 64 的情况下，才会执行转换红黑树操作，以减少搜索时间。否则，就是只是对数组扩容。
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
// 树化--》真的形成树形结构
treeifyBin(tab, hash);
// 跳出循环
break;
}
// 判断链表中结点的key值与插入的元素的key值是否相等
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
// 相等，跳出循环
break;
// 用于遍历桶中的链表，与前面的e = p.next组合，可以遍历链表
p = e;
}
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize();
else if ((e = tab[index = (n - 1) & hash]) != null) {
TreeNode<K,V> hd = null, tl = null;
// 双向链表的构建过程--由于维护双向链表比较容易，而维护红黑树比较耗费资源
do {
TreeNode<K,V> p = replacementTreeNode(e, null);
if (tl == null)
hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
if ((tab[index] = hd) != null)
hd.treeify(tab); // 真的形成树形结构
}
存在的问题(多线程环境)
JDK1.7:
多线程环境下会形成环形链表
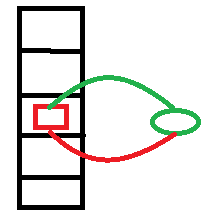
JDK1.8:
多线程环境下会有数据丢失的问题
拉链法
重hash、开放地址、溢出区、链地址法(拉链法)解决hash冲突。
“拉链法” 是：将链表和数组相结合。也就是说创建一个链表数组，数组中每一格就是一个链表。若遇到哈希冲突，则将冲突的值加到链表中即可--解决hash冲突
扰动函数
扰动函数指的是 HashMap 的 hash 方法。使用 hash 方法也就是扰动函数是为了防止一些实现比较差的 hashCode() 方法 换句话说使用扰动函数之后可以减少碰撞,
通过一定的散列函数，把一个不固定长度的输入，转成一个固定长度的输出，输出结果就是hash.
哈希表：存储哈希值的数组--存取散列值的容器（通过数组的索引存储值）
需要一个映射：hash-->函数-->对应的索引
哈希函数：将哈希值通过某种运算得到对应的数组index.
JDK1.7和JDK1.8类似，JDK1.7采用函数的方式，JDK1.8直接放在了方法里面：
static int indexFor(int h, int length){
// length是map中数组的长度
// 数组长度的规则--2的幂次方数
return h & (length - 1);
}
基本结构
Node节点类源码
static class Node<K,V> implements Map.Entry<K,V> {
// 哈希值，存放元素到hashmap中时与其它元素hash值比较
final int hash;
// 键
final K key;
// 值
V value;
// 指向下一个节点
Node<K,V> next;
}
树节点类源码
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
TreeNode<K,V> parent; // 父
TreeNode<K,V> left; // 左
TreeNode<K,V> right; // 右
TreeNode<K,V> prev; // 双向链表--便于迁移needed to unlink next upon deletion
boolean red; // 判断颜色
TreeNode(int hash, K key, V val, Node<K,V> next) {
super(hash, key, val, next);
}
// 返回根节点
final TreeNode<K,V> root() {
for (TreeNode<K,V> r = this, p;;) {
if ((p = r.parent) == null)
return r;
r = p;
}
JDK1.8之前结构
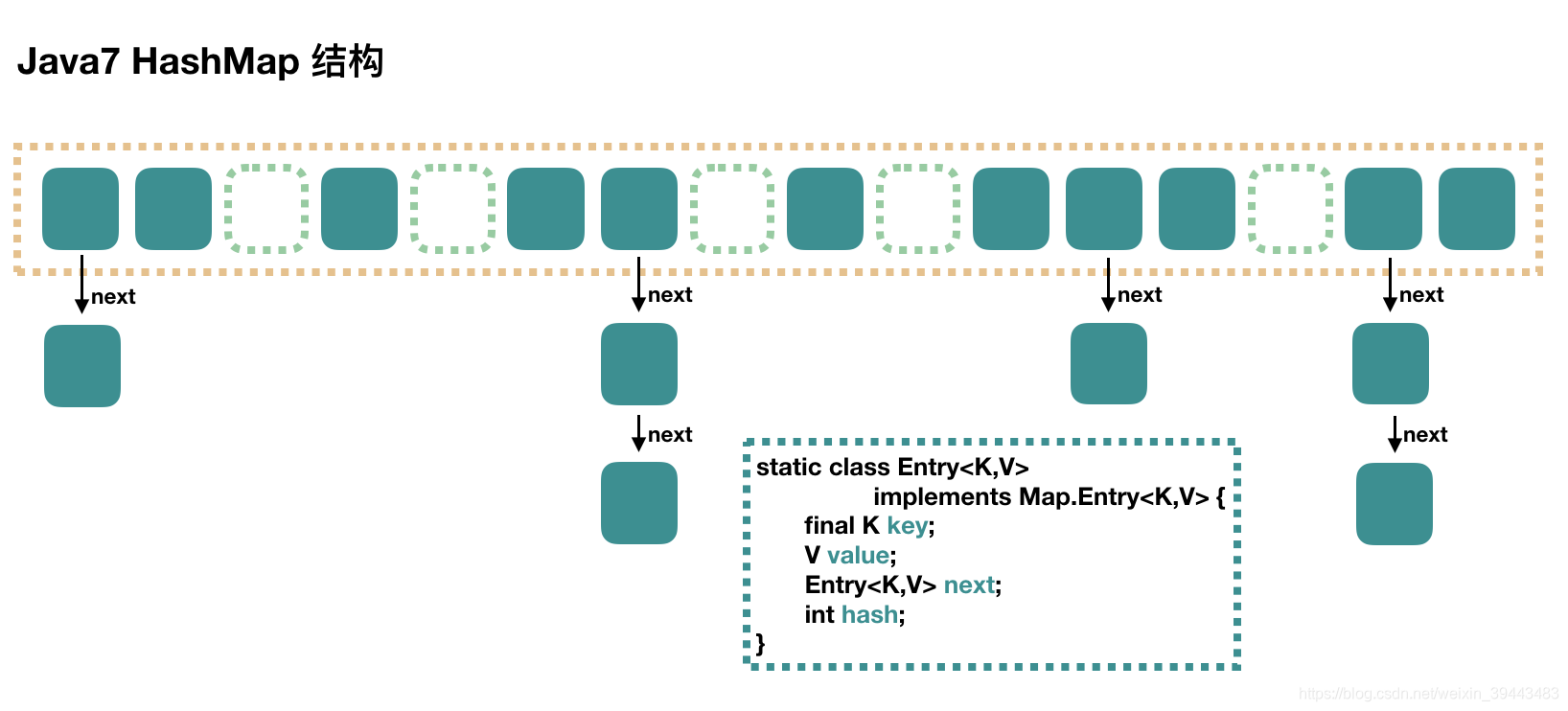
JDK1.7中的HashMap的hash方法：
static int hash(int h) {
// ^(异或)为了保留更多的信息
h ^= (h >>> 20) ^ (h >>> 12);
return h ^ (h >>> 7) ^ (h >>> 4);
}
和0做异或保持原值不变，和1做异或得到原值的相反值
a = a ^ b; b = b ^ a; a = a ^ b; 仅用2个变量完成变量交换[a = a0 ^ b0 || b = b0 ^ (a0 ^ b0)->b = a0 || a = (a0 ^ b0) ^ a0 -> a = b0]
JDK1.8之后结构
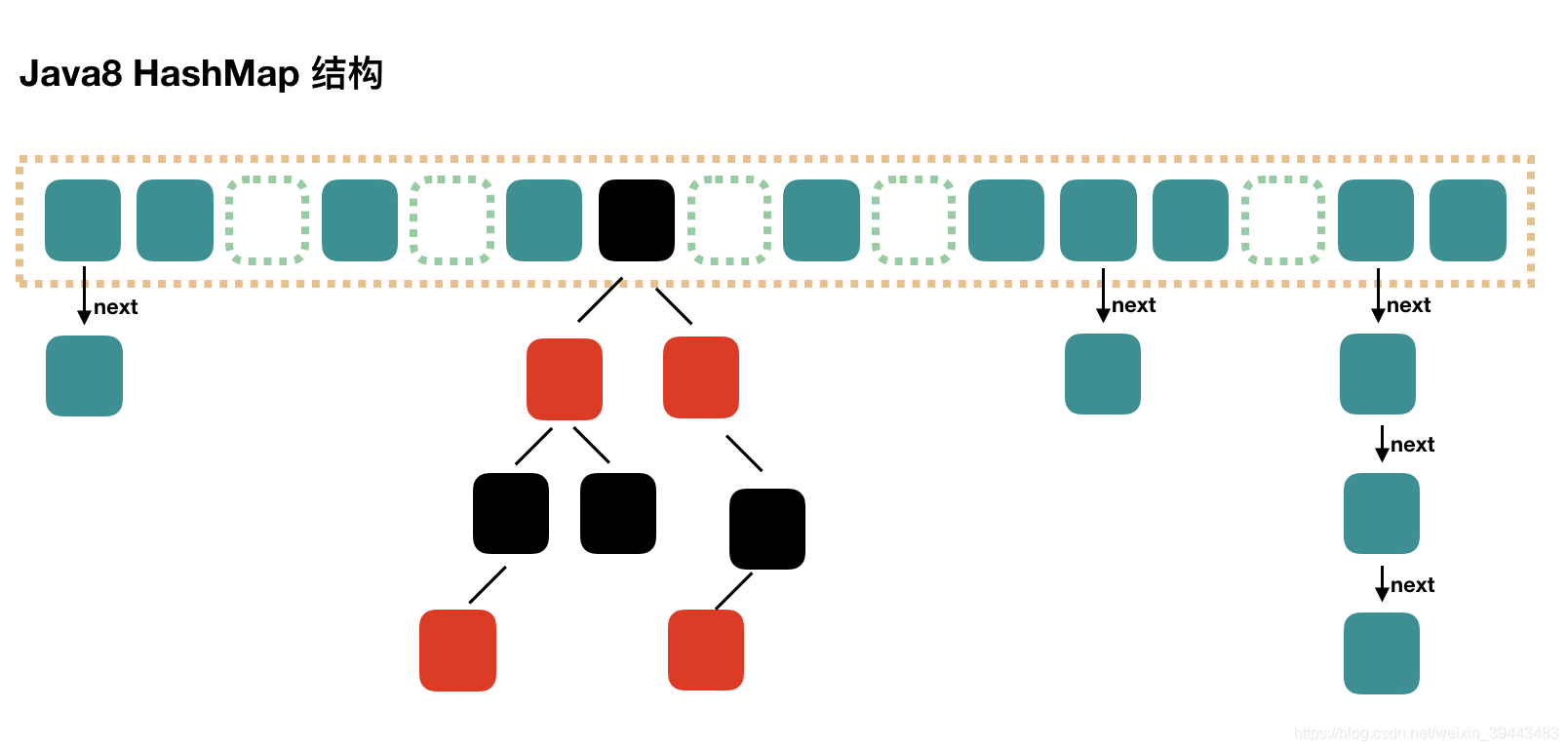
JDK1.8中的HashMap的hash方法：
static final int hash(Object key) {
int h;
// key.hashCode()：返回散列值也就是hashcode
// ^ ：按位异或
// >>>:无符号右移，忽略符号位，空位都以0补齐
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
put方法
JDK1.8之前
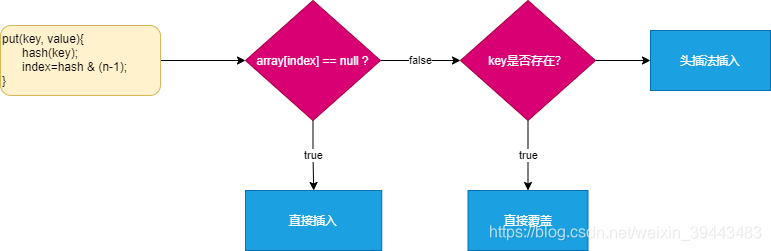
public V put(K key, V value) {
//HashMap允许存储null键，存储在数组的0索引位置
if (key == null)
return putForNullKey(value);
//内部通过一个扰乱算法获得一个hash值，用于计算数组索引
int hash = hash(key);
//计算数组索引
int i = indexFor(hash, table.length);
//判断是否是重复键
for (Entry<K,V> e = table[i]; e != null; e = e.next) {
Object k;
if (e.hash == hash && ((k = e.key) == key || key.equals(k))) {
V oldValue = e.value;
e.value = value;
e.recordAccess(this);
return oldValue;
}
}
modCount++;
//添加元素
addEntry(hash, key, value, i);
return null;
}
void addEntry(int hash, K key, V value, int bucketIndex) {
//元素个数大于阈值，同时当前索引位有值，就会执行扩容操作
if ((size >= threshold) && (null != table[bucketIndex])) {
//2倍扩容
resize(2 * table.length);
hash = (null != key) ? hash(key) : 0;
//重新计算索引位置
bucketIndex = indexFor(hash, table.length);
}
//基于键值创建Entry节点，并以头插法存入对应位置
createEntry(hash, key, value, bucketIndex);
}
JDK1.8之后
public V put(K key, V value) {
// hash(key) 计算hash值，用于计算索引
return putVal(hash(key), key, value, false, true);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
// table未初始化或者长度为0，进行扩容
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
// (n - 1) & hash 确定元素存放在哪个桶中，桶为空，新生成结点放入桶中(此时，这个结点是放在数组中)--相当于indexFor(int h, int len)这个方法
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
// 桶中已经存在元素
else {
Node<K,V> e; K k;
// 比较桶中第一个元素(数组中的结点)的hash值相等，key相等
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
// 将第一个元素赋值给e，用e来记录
e = p;
// hash值不相等，即key不相等；为红黑树结点
else if (p instanceof TreeNode)
// 放入树中
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
// 为链表结点
else {
// 在链表最末插入结点
for (int binCount = 0; ; ++binCount) {
// 到达链表的尾部
if ((e = p.next) == null) {
// 在尾部插入新结点
p.next = newNode(hash, key, value, null);
// 结点数量达到阈值(默认为 8 )，执行 treeifyBin 方法
// 这个方法会根据 HashMap 数组来决定是否转换为红黑树。
// 只有当数组长度大于或者等于 64 的情况下，才会执行转换红黑树操作，以减少搜索时间。否则，就是只是对数组扩容。
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
// 跳出循环
break;
}
// 判断链表中结点的key值与插入的元素的key值是否相等
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
// 相等，跳出循环
break;
// 用于遍历桶中的链表，与前面的e = p.next组合，可以遍历链表
p = e;
}
}
// 表示在桶中找到key值、hash值与插入元素相等的结点
if (e != null) {
// 记录e的value
V oldValue = e.value;
// onlyIfAbsent为false或者旧值为null
if (!onlyIfAbsent || oldValue == null)
//用新值替换旧值
e.value = value;
// 访问后回调
afterNodeAccess(e);
// 返回旧值
return oldValue;
}
}
// 结构性修改
++modCount;
// 实际大小大于阈值则扩容
if (++size > threshold)
resize();
// 插入后回调
afterNodeInsertion(evict);
return null;
}
get方法
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
// 数组元素相等
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
// 桶中不止一个节点
if ((e = first.next) != null) {
// 在树中get
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
// 在链表中get
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}
扫一扫
1912
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
