李宏毅2021春季机器学习课程视频笔记5-模型训练不起来问题(当梯度很小的时候问题)

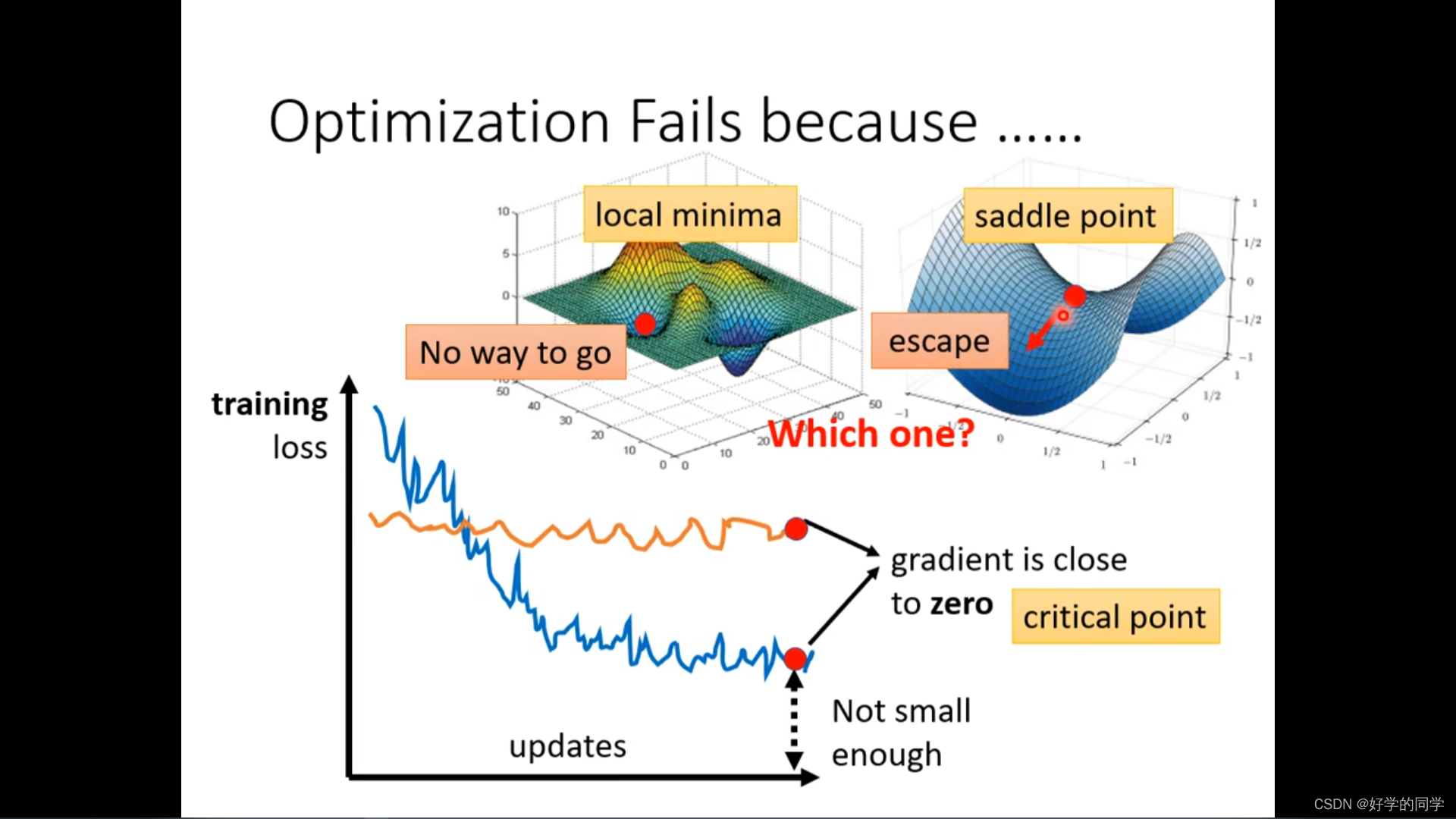
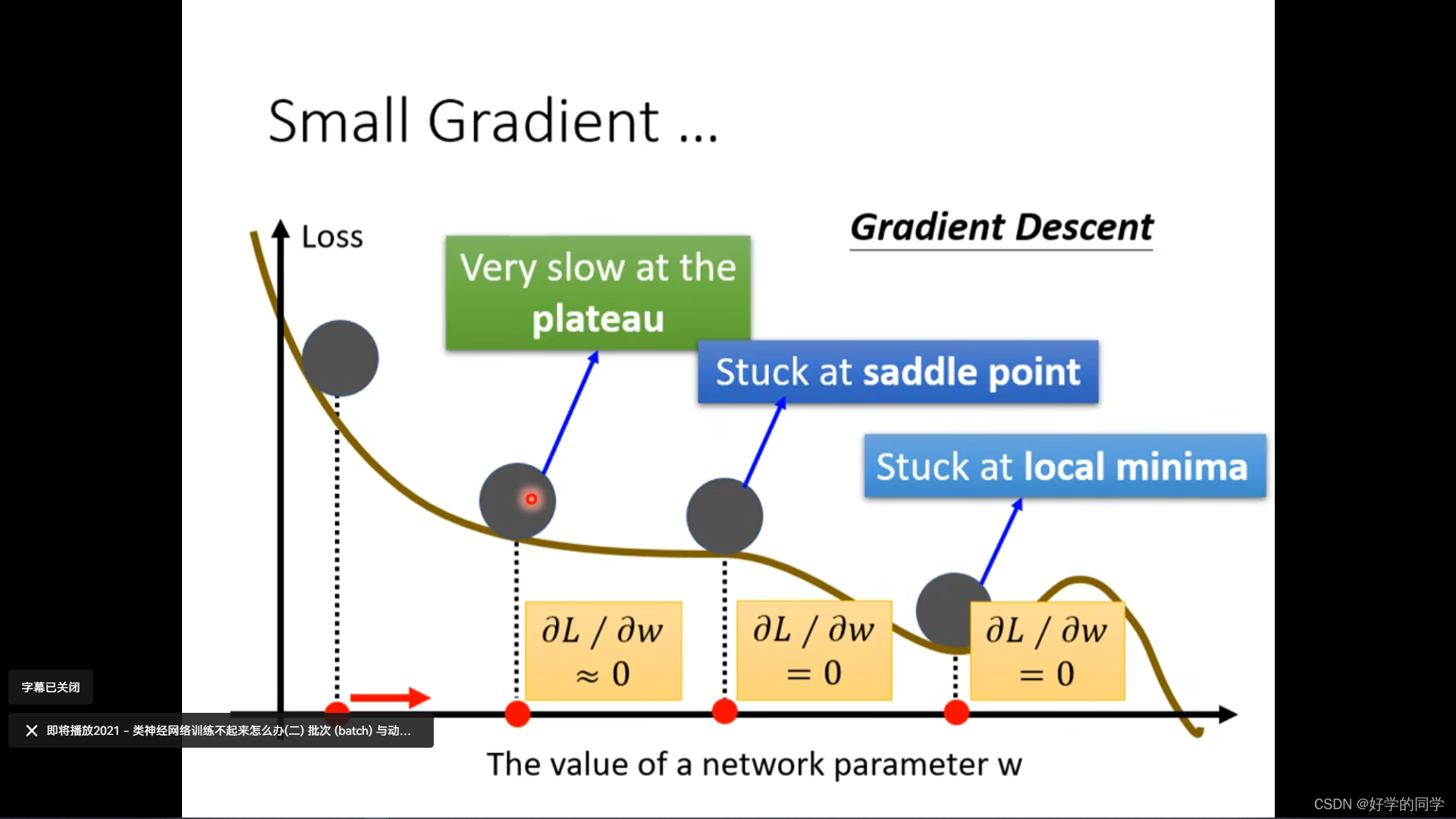
 求解最小Loss的失败，不能得到最优的值，找不到Loss足够小的值。

•  1.Loss关于参数的梯度为0，不能继续更新参数。（local minima 或者 saddle point）

如何知道走到了哪个点？

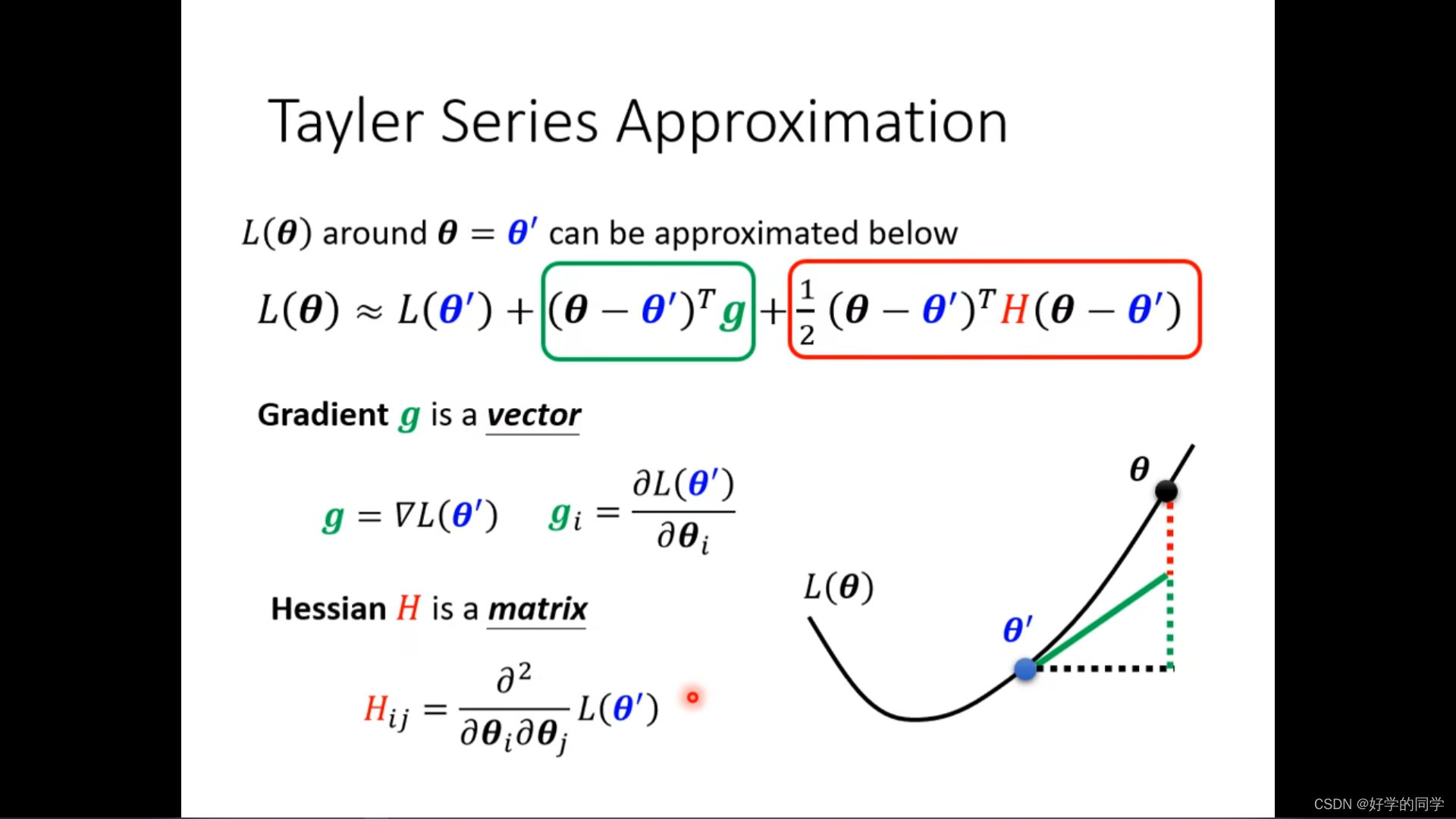
 利用泰勒展开：

 Critical Point的一阶导数为0。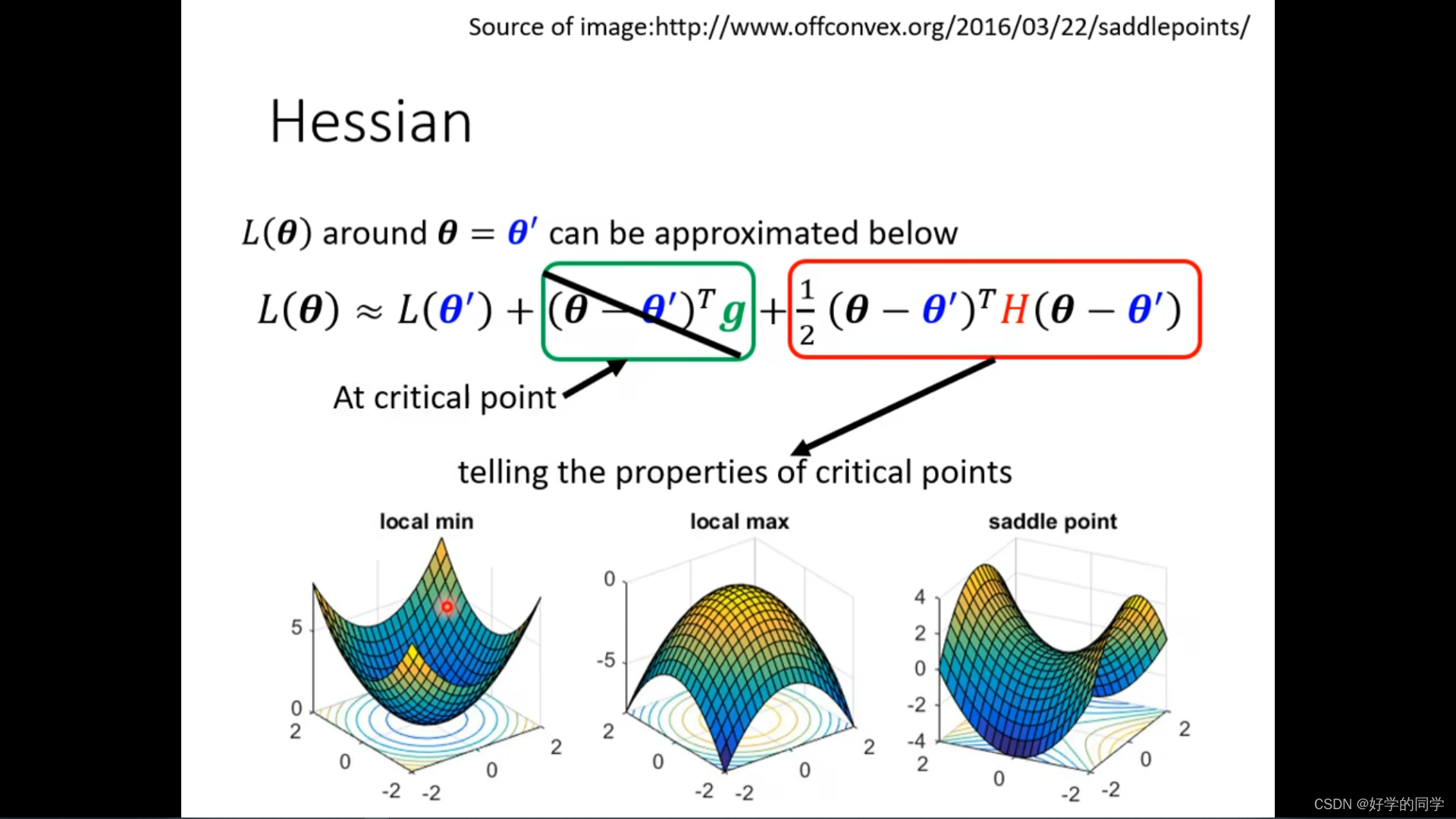

 

 举例子（Example）：

 

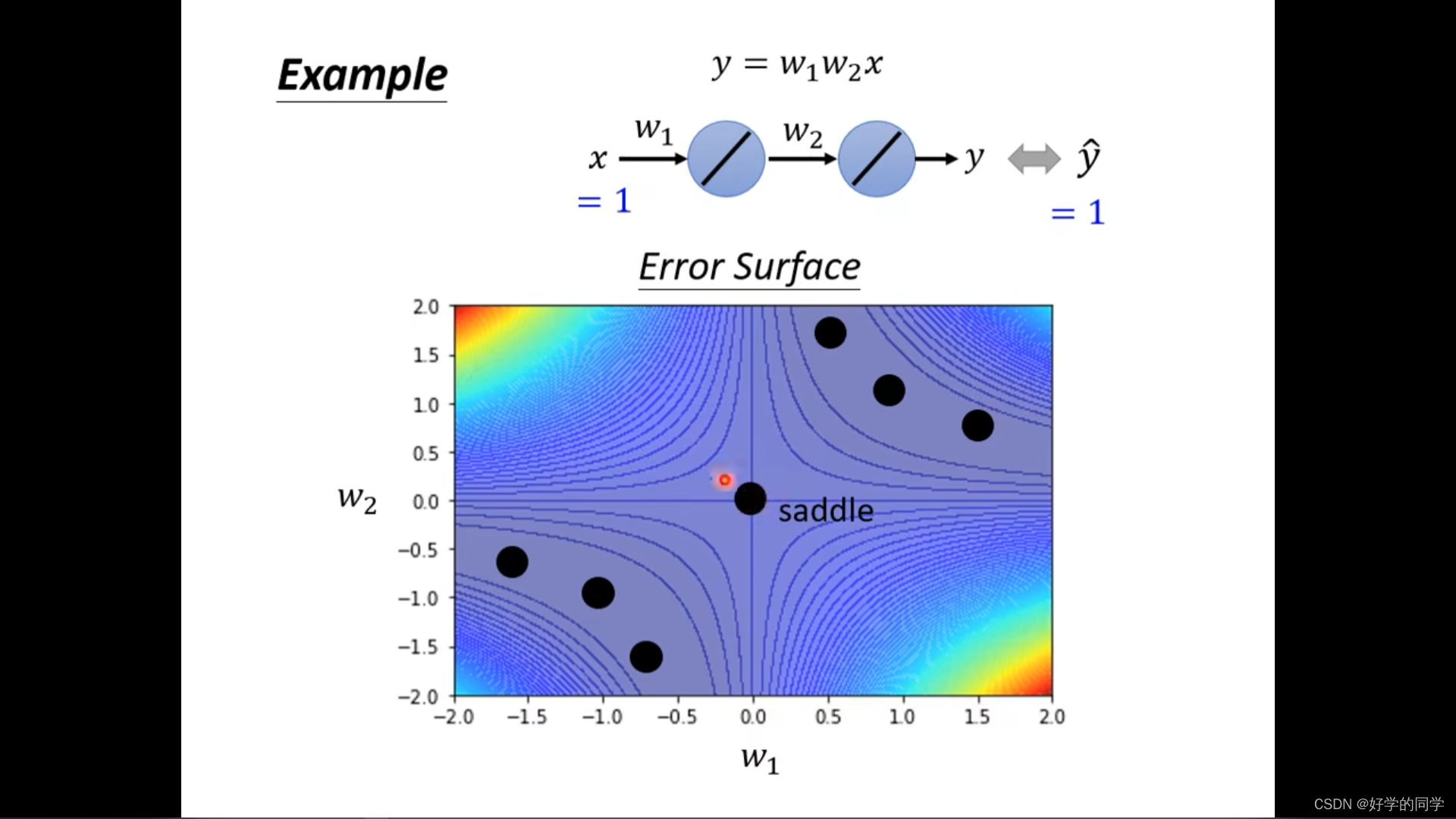
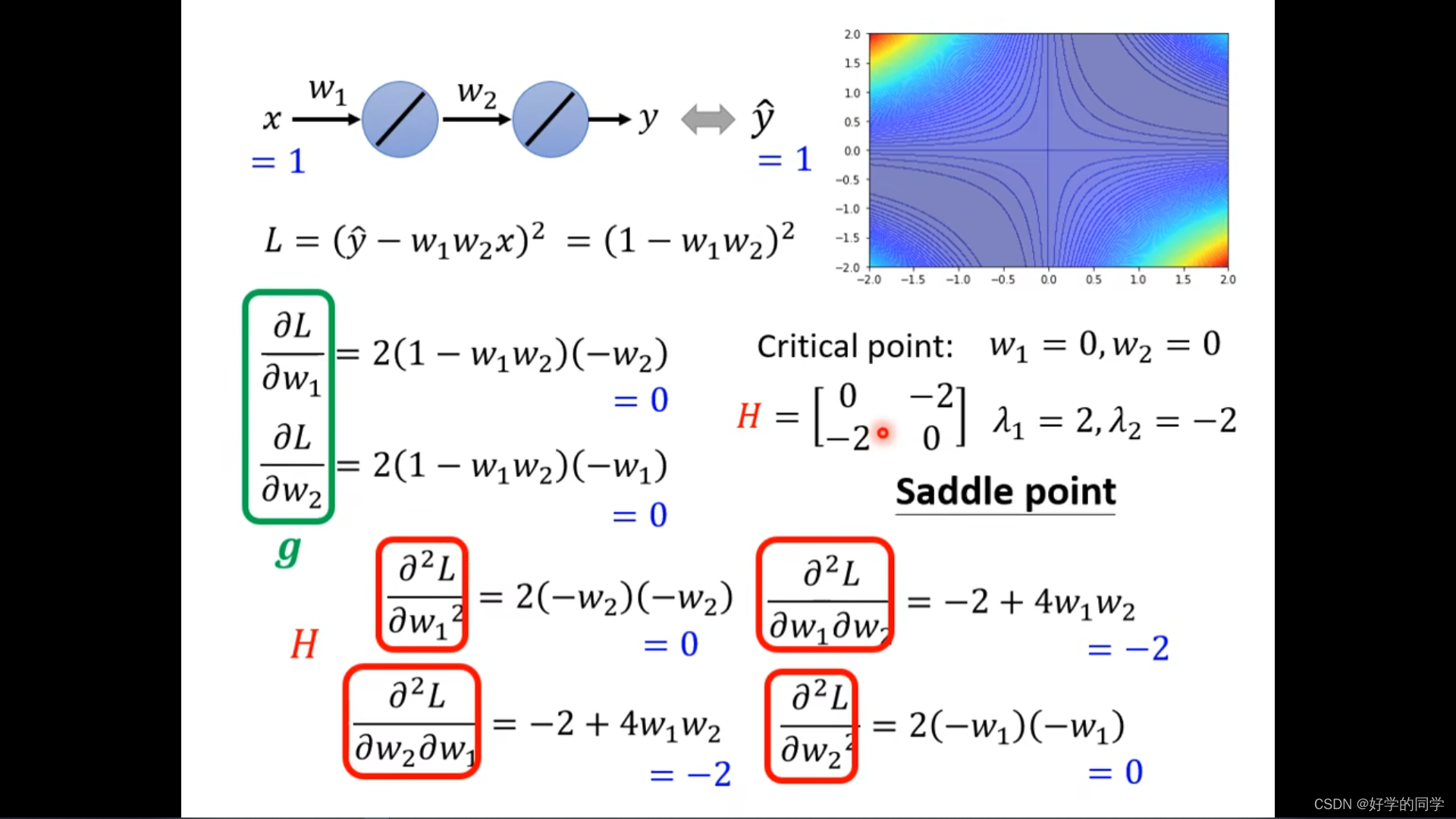
 不需要担心Saddle Point，因为Hessian矩阵会告诉我们参数更新的方向。

 

 

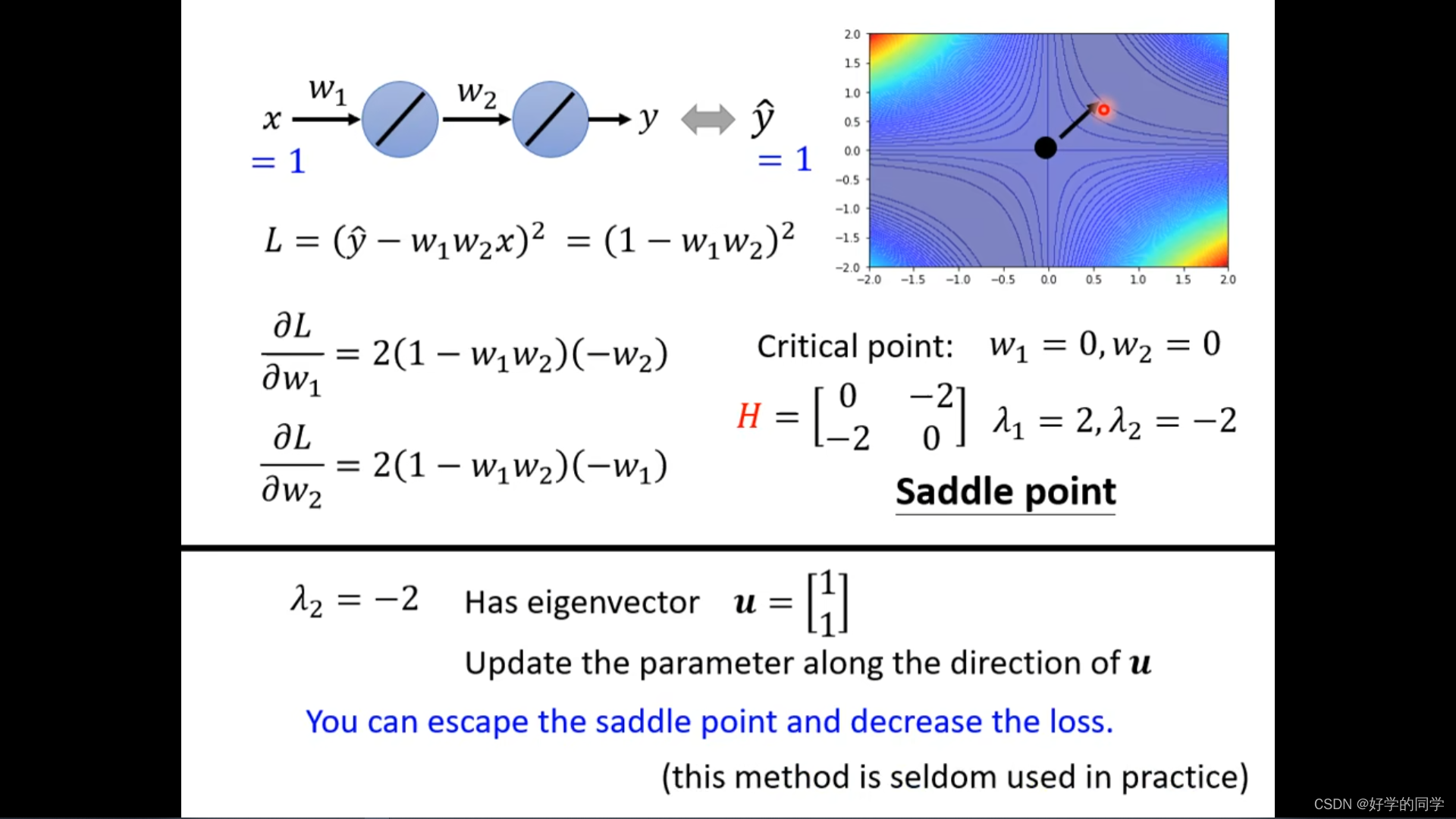
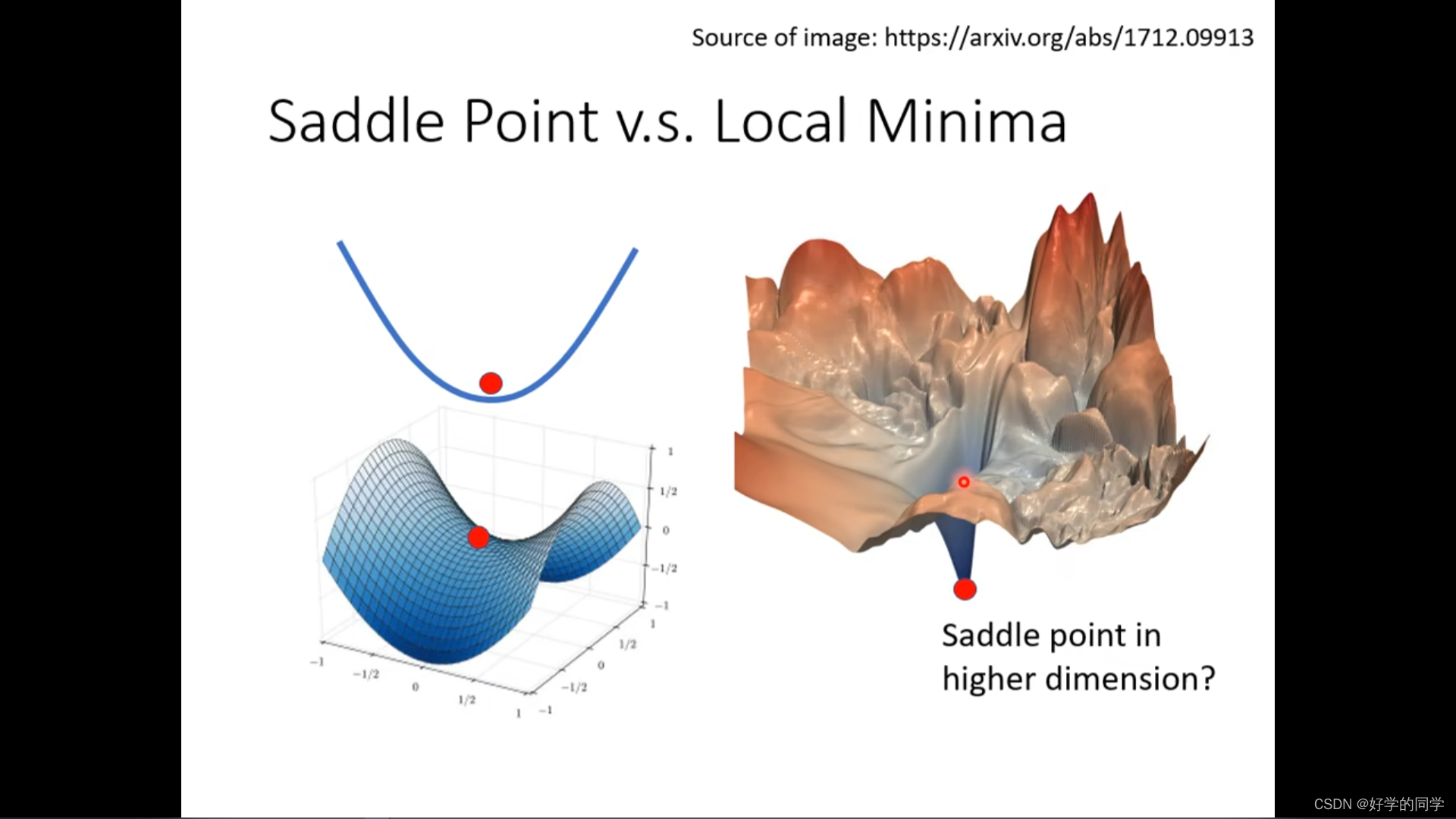
 Saddle Point V.S. Local Minima

 

 三维空间这个石棺是封闭的，但是在高维空间里石棺可能是非封闭的，取到里面的东西。推广到损失函数形状，在二维空间中可能是一个Local Minima，但是转换到三位空间中其可能就是一个Saddle Point。

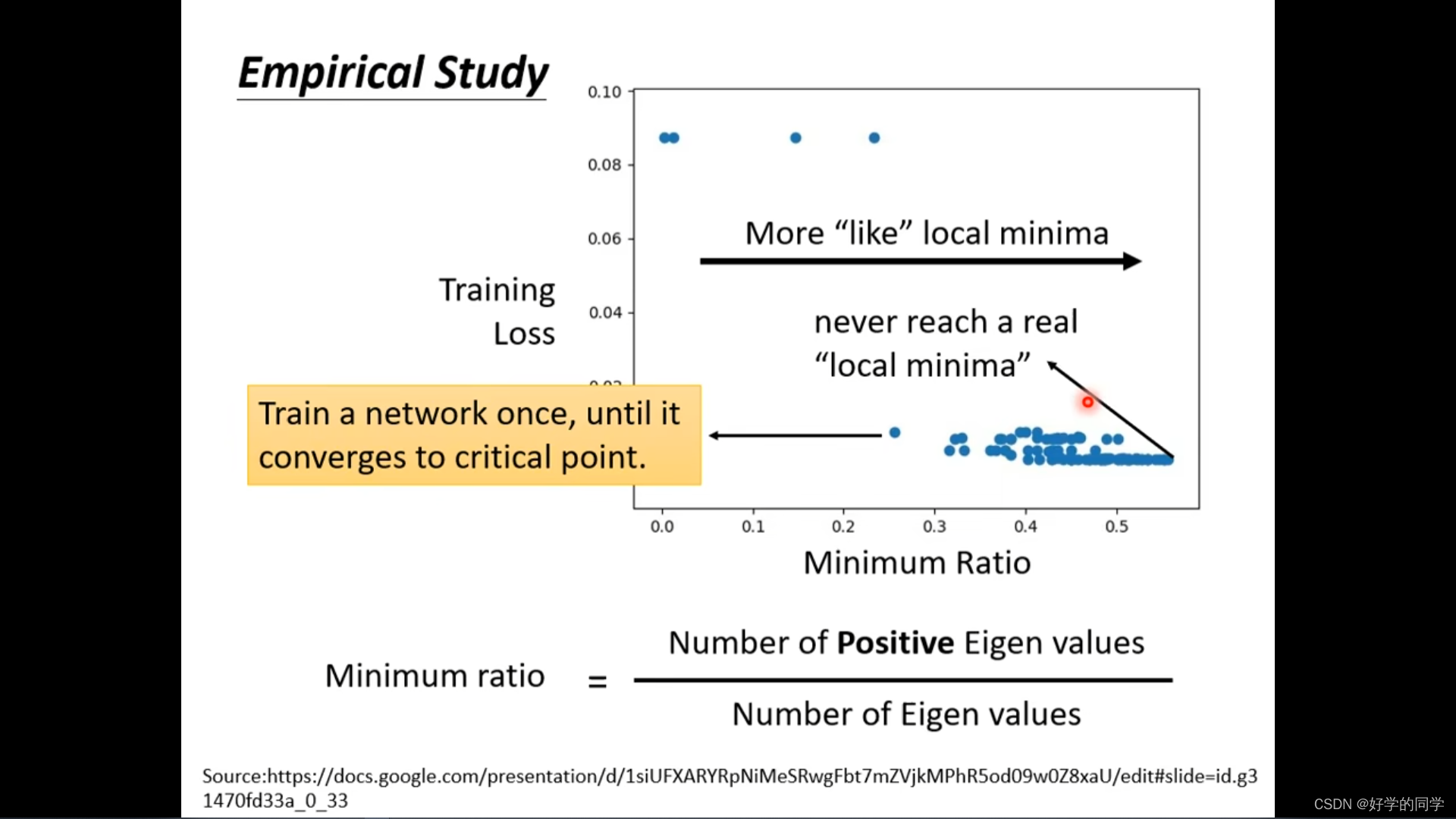
 实际研究，当所有的Hessian矩阵的Eigen Value都大于0时，表明这一点为Local Minima，如果有小于0的Value就表明这是一个Saddle Point。实际实验表明Local Minima最少，大多数为Saddle Point。