《3D Graph Neural Networks for RGBD Semantic Segmentation》论文笔记
pytorch实现的代码:
https://github.com/yanx27/3DGNN_pytorch
一、摘要
随着深度传感器的发展,RGBD语义分割被应用于许多问题上,如:虚拟现实,机器人以及人机交互等等。与现有的2D语义分割相比,RGBD语义分割可以通过探索深度信息来利用现实世界的几何信息辅助分割。如下图所示,在常规的2D图像上,桌子会和微波炉在像素上非常接近,但是在3D的世界中,却不存在这种误区,因为这些像素点在3D点云中距离很遥远。

也有许多方法是将RGBD分割和2D分割一样来做,将深度图片当做一种输入图片,用神经网络分别对这两个图像(RGB和深度图)进行特征的提取。这种做法需要两个CNN,使得计算量和显存使用都变成了原来的两倍。而整合时内容上的缺失,可能也会导致错误,如下图所示:2D的CNN模型会将table 误认为是 counter。
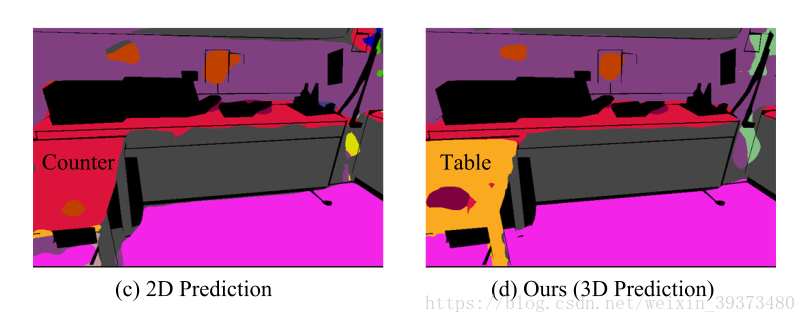
另一种方法是利用3D CNN来处理,但是也有一定的局限性:由于3D点云非常稀疏,因此从这些数据中学习有效得学习非常困难。 此外,3D CNN在计算成本上比2D CNN更加大,因此难以扩展到处理大量点云。
为了解决上述的挑战,论文提出一种端到端的 3D Graph Neural Network,来直接从3D点云中学习其表示。首先根据深度图像将2D像素转化为3D,然后用一元特征向量将每个3D点连接起来,相当于2D语义分割FCN的输出
(
x
i
,
y
i
,
d
e
p
t
h
i
)
(x_i,y_i,depth_i)
(xi,yi,depthi)。然后构建一个图(graph),其结点(nodes)是3D的点,边缘(edges)是从3D空间中找到的最近邻的点。对于每一个结点,论文将图像特征向量作为初始的表达,然后用一个循环函数来迭代更新它。这个动态计算机制的核心想法是:每个结点的状态不仅取决于它的历史状态,还取决于他周围的点,即既考虑其形状也考虑其3D的信息。
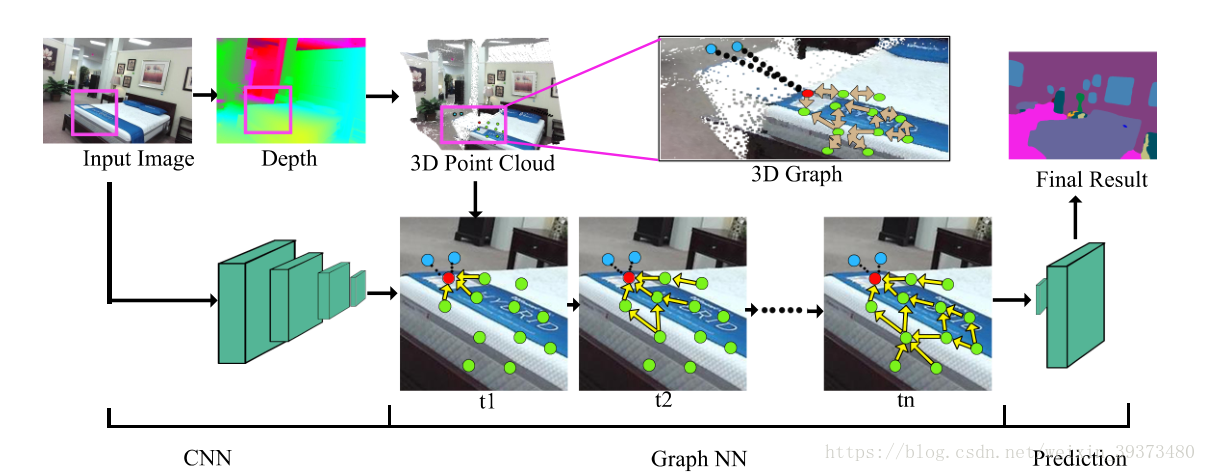
图中的第一部分首先将RGB图片和深度图片变为3D点云,第二部分其通过点云构建图(graph)。下半部分的图中蓝色的点和黑色的线代表着由2D图像构造的结点(node)和边(edge),很明显从三维点云中编码的几何信息是难以从2D图像中推断的。在底部,连接红点的子图代表着传播的过程,黄色边缘表明红点在不同时间步骤中接收的信息来源。
论文用每一个结点的最终状态来作为每个结点的分类。梯度则由CNN来进行端到端的训练。实验结果表明:NYUD2和SUN-RGBD数据集上,取得了极好的分割效果。
二、Graph Neural Networks的详述
图神经网络(Graph Neural Networks)是一种可以直接对有向图、无向图、循环图等图数据直接进行训练的神经网络。传统的神经网络一般会通过一个传导函数(transduction function)将图结构和构成图的点映射到M维的欧式空间中。
一般来讲,我们会希望构建一个传导函数 τ \tau τ将有 n n n个结点的图数据 G G G映射成一个向量,其中 τ ( G , n ) ∈ R m \tau(G,n)\in R^m τ(G,n)∈Rm。我们可以根据其与不与 n n n有关分为两大类:
- Graph focused:传导函数与点(node)无关,并且在图形结构化数据集上实现分类器或回归器。
- Node focused:传导函数与点(node)有关,分类器或归类器取决于每个点的属性(property)。
因此我们可以将分类或者分割问题转换成对每一个结点的类别预测,比如说下图中属于房子的点我们预测出为1(黑点),而不属于房子的点预测成-1(白点),这就是图数据的最初处理想法。
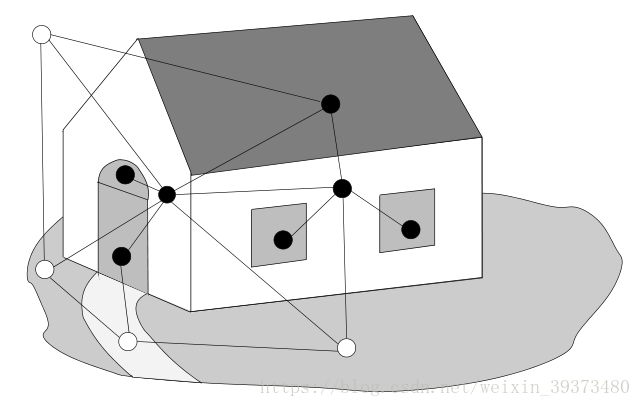
传统的方法一般通过RNN对Graph focused的图数据进行训练,但在转换过程中其可能会丢弃很多图的拓扑结构,而文章的方法结合了RNN和马尔科夫链,可以同时针对 Graph focused 和 Node focused 进行训练。
图结构数据由 G ( N , E ) G(N,E) G(N,E)表示, N N N是点的集合而 E E E是边的集合。 n e [ n ] ne_{[n]} ne[n]表示点 n n n的邻结点。 c o [ n ] co_{[n]} co[n]表示和结点 n n n连接的边。 l n l_n ln和 l ( n 1 , n 2 ) l_{(n1,n2)} l(n1,n2)表示n的标签以及边的标签。而 L L L表示整个图结构数据中所有的标签。这个模型(GNN)考虑的图结构数据分为非位置图(Non-positional graph)和位置图(positional graph)。非位置图可以理解成一般的图,在这里着重说明下位置图:在位置图中,对每个结点而言,存在一个内部映射函数(injective function) u n : n e [ n ] → { 1 , . . . , ∣ N ∣ } u_n:ne[n]\rightarrow\{1,...,|N |\} un:ne[n]→{1,...,∣N∣}。它为 n n n(图中任意一个结点)的邻结点分配不同的位置。邻结点的位置可以隐含地用于存储有用的信息。比如:可以用这个来表示某一点的邻接点在顺时针(或逆时针)的意义上的次序,或者重要性的排序。
GNN的核心思想便是用结点表示物体的类别而用边表示他们的关系。图结构数据中,我们可以用 X n X_n Xn来表示一个点的状态,其由邻结点的信息以及边的信息而决定,其数学表达等式如下:
x n = f w ( l n , x n e [ n ] , l n e [ n ] ) , n ∈ N x_n = f_w (l_n ,x_{ne_[n]} ,l_{ne_[n]}), n \in N xn=fw(ln,xne[n],lne[n]),n∈N
其中
l
n
,
x
n
e
[
n
]
,
l
n
e
[
n
]
l_n ,x_{ne_[n]} ,l_{ne_[n]}
ln,xne[n],lne[n]是结点
n
n
n的标签、邻结点的状态和标签。
f
w
f_w
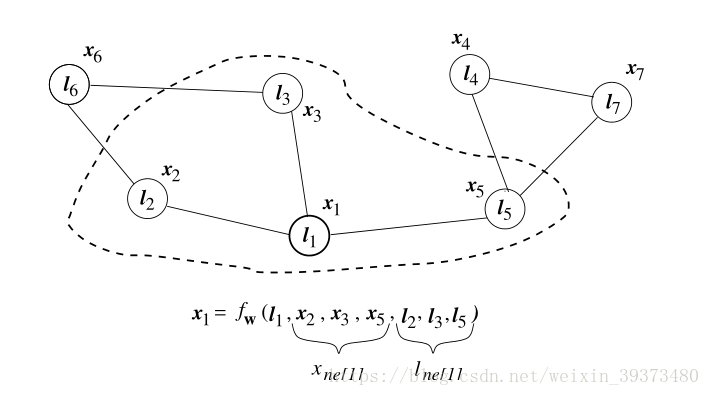
fw是一个包含参数的方程,称为局部过渡函数(local transition function)。如下图,
x
1
x_1
x1的状态就是与其本身的标签,以及其邻结点的状态和标签有关。
对于每一个结点
n
n
n,我们同样可以定义其局部输出函数(local output function)
o
n
∈
R
m
o_n \in R^m
on∈Rm。其表达式如下:
o n = g w ( x n , l n ) , n ∈ N o_n = g_w (x_n ,l_n ), n \in N on=gw(xn,ln),n∈N
最终,我们让 x x x和 l l l表示所有的结点和结点标签的集合,我们可以得到全局过渡函数 (global transition function)和全局输出函数 (global output function)
x = F w ( x , l ) o = G w ( x , l ) x = F_w (x,l) \\o = G_w (x,l) x=Fw(x,l)o=Gw(x,l)
上面这两个等式有唯一解的条件是 F w F_w Fw是一个收缩映射(contraction map),并且存在 μ , 0 < μ < 1 μ,0<μ<1 μ,0<μ<1,对于任何的 x , y x,y x,y使得接下来的不等式满足:
∣ ∣ F w ( x , l ) − F w ( y , l ) ∣ ∣ ≥ μ ∣ ∣ x − y ∣ ∣ ||F_w(x,l)-F_w(y,l)||\geq\mu ||x-y|| ∣∣Fw(x,l)−Fw(y,l)∣∣≥μ∣∣x−y∣∣
这里 x , y x,y x,y表示图结构数据中的任意两个节点。(这一点之前的文章已经证明出来了)
-
若对于非位置图(Non-positional graph),其点的状态可以被替换成一下形式:
x n = ∑ u ∈ n e n h w ( l n , x u , l u ) , n ∈ N x_n = \sum_{u\in ne_{n} }h_w(l_n ,x_{u} ,l_{u}), \ n \in N xn=u∈nen∑hw(ln,xu,lu), n∈N
每个点的状态只与周围的一个点的状态和标签以及自己的标签有关,这其实类似于RNN的基本原理。这里的 h w h_w hw可以用线性(Linear GNN)或者网络(Neural GNN)两种形式。 -
能够处理位置图(positional graph)便是GNN最大的优势,我们可以通过最小化下列式子来得到理想的output:(其中 ϕ w ( G , n ) = o n \phi_w (G,n) = o_n ϕw(G,n)=on, t t t为真实标签)
e w = ∑ i = 1 p ( t i − ϕ w ( G i , n i ) ) 2 e_w = \sum_{i=1}^p(t_i-\phi_w(G_i,n_i))^2 ew=i=1∑p(ti−ϕw(Gi,ni))2
因此我们引入时间
t
t
t,通过迭代下述公式找到全局最优点:
x
n
(
t
+
1
)
=
f
w
(
l
n
,
x
n
e
[
n
]
(
t
)
,
l
n
e
[
n
]
)
,
o
n
(
t
+
1
)
=
g
w
(
x
n
(
t
+
1
)
,
l
n
)
,
n
∈
N
x_n (t + 1) = f_w (l_n ,x_{ne_{[n]}} (t),l_{ne_{[n]}} ),\\ o_n (t + 1) = g_w (x_n (t + 1),l_n ), \\n \in N
xn(t+1)=fw(ln,xne[n](t),lne[n]),on(t+1)=gw(xn(t+1),ln),n∈N
上述式子被称为编码网络(encoding network)
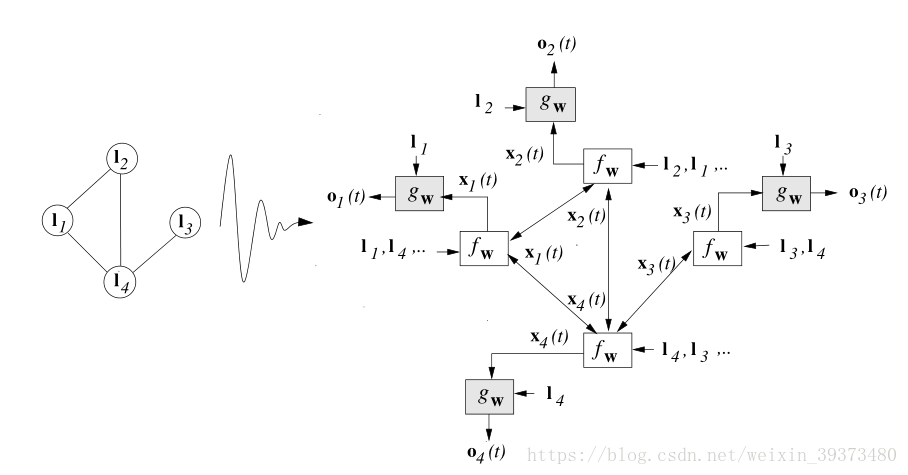
可以从图中看出,编码网络有
f
w
f_w
fw和
g
w
g_w
gw两类单元组成,每一个结点储存着当前
x
n
(
t
)
x_n(t)
xn(t)的状态信息,当我们激活这些单元时,他便会去计算
x
n
(
t
+
1
)
x_n(t+1)
xn(t+1)。至于反向传播依然是采用梯度下降的方法,类似于RNN的Back-propagation through time (BPTT),这里不给予过多解释。
三、如何用GNN做语义分割
Graph Construction
首先,通过2D的像素图和一张深度图,我们可以构造一个有向图。令 [ x , y , z ] [x,y,z] [x,y,z]为坐标系中的3D坐标。利用这些点构建一个图(graph),其结点(nodes)是3D坐标上的点,边缘(edges)是从3D空间中找到的K最近邻的点。
Propagation Model
对于每一个结点,论文将图像特征向量作为初始的表达,然后用上述的GNN来迭代更新它。这个动态计算机制的核心想法是:每个结点的状态不仅取决于它的历史状态,还取决于他周围的点,即既考虑其形状也考虑其3D的信息。 最终用收敛时结点的状态作为这个点的标签进行语义分割。
Prediction Model
文中列出了在 NYUD2数据集的表现:
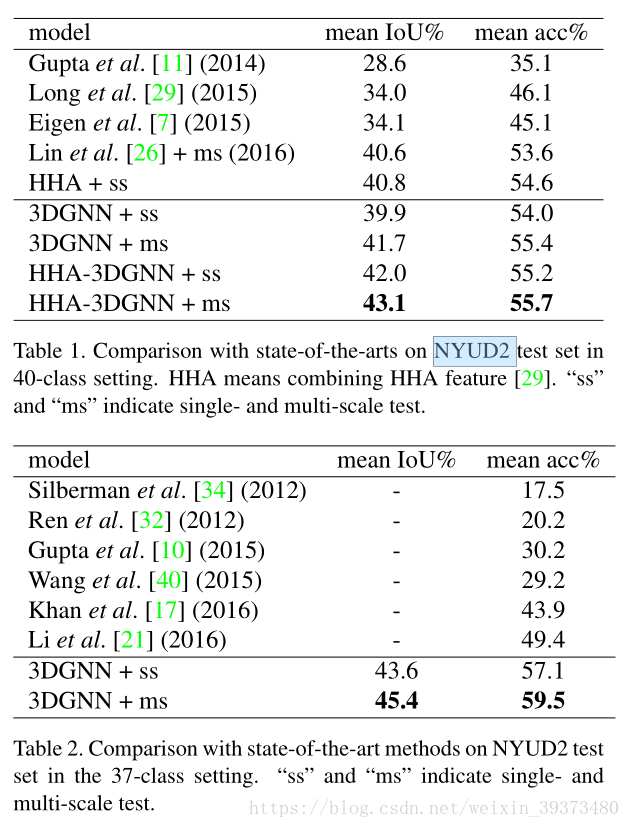





 本文探讨了一种创新的3D图神经网络(GNN)方法,用于RGBD语义分割任务。该方法直接从3D点云中学习表示,通过构建图结构,将图像特征向量作为初始表达,利用GNN迭代更新,充分考虑3D信息和形状特征,最终用于语义分割。在NYUD2和SUN-RGBD数据集上取得了显著的效果。
本文探讨了一种创新的3D图神经网络(GNN)方法,用于RGBD语义分割任务。该方法直接从3D点云中学习表示,通过构建图结构,将图像特征向量作为初始表达,利用GNN迭代更新,充分考虑3D信息和形状特征,最终用于语义分割。在NYUD2和SUN-RGBD数据集上取得了显著的效果。
















 324
324

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








