JavaScript深入系列之浮点数精度

前言

0.1+0.2是否等于0.3作为一道经典的面试题，已经广外熟知，说起原因，大家能回答出这是浮点数精度问题导致，也能辩证的看待这并非是ECMAScript这门语言的问题，今天就是具体看一下背后的原因。

数字类型

ECMAScript中的Number类型使用IEEE754标准来表示整数和浮点数值。所谓IEEE754标准，全称IEEE二进制浮点数算术标准，这个标准定义了表示浮点数的格式等内容。

在IEEE754中，规定了四种表示浮点数值的方式：单精确度（32位）、双精确度（64位）、延伸单精确度、与延伸双精确度。像ECMAScript采用的就是双精确度，也就是说，会用64位字节来储存一个浮点数。

浮点数转二进制

我们来看下1020用十进制的表示：

1020 = 1 10^3 + 0 10^2 + 2 10^1 + 0 10^0

所以1020用十进制表示就是1020……(哈哈)

如果1020用二进制来表示呢？

1020=1 2^9+1 2^8+1 2^7+1 2^6+1 2^5+1 2^4+1 2^3+1 2^2+0 2^1+0 2^0

所以1020的二进制为1111111100

那如果是0.75用二进制表示呢？同理应该是：

0.75=a 2^-1+b 2^-2+c 2^-3+d 2^-4+...

因为使用的是二进制，这里的abcd……的值的要么是0要么是1。

那怎么算出abcd……的值呢，我们可以两边不停的乘以2算出来，解法如下：

0.75=a 2^-1+b 2^-2+c 2^-3+d 2^-4...

两边同时乘以2

1+0.5=a 2^0+b 2^-1+c 2^-2+d 2^-3...(所以a=1)

剩下的：

0.5=b 2^-1+c 2^-2+d*2^-3...

再同时乘以2

1+0=b2^0+c2^-2+d*2^-3...(所以b=1)

所以0.75用二进制表示就是0.ab，也就是0.11

然而不是所有的数都像0.75这么好算，我们来算下0.1：

0.1 = a * 2^-1 + b * 2^-2 + c * 2^-3 + d * 2^-4 + ...

0 + 0.2 = a * 2^0 + b * 2^-1 + c * 2^-2 + ... (a = 0)

0 + 0.4 = b * 2^0 + c * 2^-1 + d * 2^-2 + ... (b = 0)

0 + 0.8 = c * 2^0 + d * 2^-1 + e * 2^-2 + ... (c = 0)

1 + 0.6 = d * 2^0 + e * 2^-1 + f * 2^-2 + ... (d = 1)

1 + 0.2 = e * 2^0 + f * 2^-1 + g * 2^-2 + ... (e = 1)

0 + 0.4 = f * 2^0 + g * 2^-1 + h * 2^-2 + ... (f = 0)

0 + 0.8 = g * 2^0 + h * 2^-1 + i * 2^-2 + ... (g = 0)

1 + 0.6 = h * 2^0 + i * 2^-1 + j * 2^-2 + ... (h = 1)

....

然后你就会发现，这个计算在不停的循环，所以0.1用二进制表示就是0.00011001100110011……

浮点数的存储

虽然0.1转成二进制时是一个无限循环的数，但计算机总要储存吧，我们知道ECMAScript使用64位字节来储存一个浮点数，那具体是怎么储存的呢？这就要说回IEEE754这个标准了，毕竟是这个标准规定了存储的方式。

这个标准认为，一个浮点数(Value)可以这样表示：

Value=sign exponent fraction

sign(符号) exponent（指数） fraction（小数）

看起来很抽象的样子，简单理解就是科学计数法……

比如-1020，用科学计数法表示就是:

-1 10^3 1.02

sign就是-1，exponent就是10^3，fraction就是1.02

对于二进制也是一样，以0.1的二进制0.00011001100110011……这个数来说：

可以表示为：

1 2^-4 1.1001100110011……

其中sign就是1，exponent就是2^-4，fraction就是1.1001100110011……

而当只做二进制科学计数法的表示时，这个Value的表示可以再具体一点变成：

V=(-1)^S (1+Fraction) 2^E

(如果所有的浮点数都可以这样表示，那么我们存储的时候就把这其中会变化的一些值存储起来就好了)

我们来一点点看：

(-1)^S表示符号位，当S=0，V为正数；当S=1，V为负数。

再看(1+Fraction)，这是因为所有的浮点数都可以表示为1.xxxx*2^xxx的形式，前面的一定是1.xxx，那干脆我们就不存储这个1了，直接存后面的xxxxx好了，这也就是Fraction的部分。

最后再看2^E

如果是1020.75，对应二进制数就是1111111100.11，对应二进制科学计数法就是1 _1.11111110011 _2^9，E的值就是9，而如果是0.1，对应二进制是1 _1.1001100110011…… _2^-4，E的值就是-4，也就是说，E既可能是负数，又可能是正数，那问题就来了，那我们该怎么储存这个E呢？

我们这样解决，假如我们用8位字节来存储E这个数，如果只有正数的话，储存的值的范围是0~254，而如果要储存正负数的话，值的范围就是-127~127，我们在存储的时候，把要存储的数字加上127，这样当我们存-127的时候，我们存0，当存127的时候，存254，这样就解决了存负数的问题。对应的，当取值的时候，我们再减去127。

所以呢，真到实际存储的时候，我们并不会直接存储E，而是会存储E+bias，当用8个字节的时候，这个bias就是127。

所以，如果要存储一个浮点数，我们存S和Fraction和E+bias这三个值就好了，那具体要分配多少个字节位来存储这些数呢？IEEE754给出了标准：

 

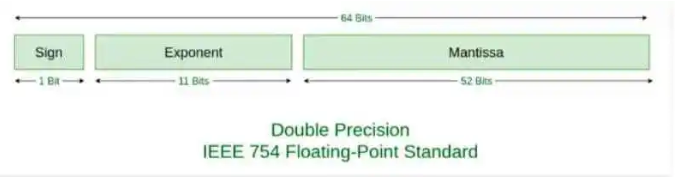
在这个标准下：

我们会用1位存储S，0表示正数，1表示负数。

用11位存储E+bias（偏差），对于11位来说，bias的值是2^(11-1)-1，也就是1023。

 

用52位存储Fraction。

举个例子，就拿0.1来看，对应二进制是1_1.1001100110011……_2^-4，Sign是0，E+bias是-4+1023=1019，1019用二进制表示是1111111011，Fraction是1001100110011……

对应64个字节位的完整表示就是：

0 011111110111001100110011001100110011001100110011001100110011010

同理,0.2表示的完整表示是：

0 011111111001001100110011001100110011001100110011001100110011010

所以当0.1存下来的时候，就已经发生了精度丢失，当我们用浮点数进行运算的时候，使用的其实是精度丢失后的数。

浮点数的运算

关于浮点数的运算，一般由以下五个步骤完成：对阶、尾数运算、规格化、舍入处理、溢出判断。我们来简单看一下0.1和0.2的计算。

首先是对阶，所谓对阶，就是把阶码调整为相同，比如0.1是1. 1001100110011……*2^-4，阶码是-4，而0.2就是1. 10011001100110...*2^-3，阶码是-3，两个阶码不同，所以先调整为相同的阶码再进行计算，调整原则是小阶对大阶，也就是0.1的-4调整为-3，对应变成0. 11001100110011……*2^-3

接下来是尾数计算:

0.1100110011001100110011001100110011001100110011001101

+ 1.1001100110011001100110011001100110011001100110011010

————————————————————————————————

 10.0110011001100110011001100110011001100110011001100111

我们得到结果为10.0110011001100110011001100110011001100110011001100111*2^-3

将这个结果处理一下，即结果规格化，变成1. 0011001100110011001100110011001100110011001100110011(1)*2^-2

括号里的1意思是说计算后这个1超出了范围，所以要被舍弃了。

再然后是舍入，四舍五入对应到二进制中，就是0舍1入，因为我们要把括号里的1丢了，所以这里会进一，结果变成

1.0011001100110011001100110011001100110011001100110100*2^-2

本来还有一个溢出判断，因为这里不涉及，就不讲了。

所以最终的结果存成64位就是

0 011111111010011001100110011001100110011001100110011001100110100

将它转换为10进制数就得到0.30000000000000004440892098500626

因为两次存储时的精度丢失加上一次运算时的精度丢失，最终导致了0.1+0.2!==0.3

其他

//十进制转二进制

parseFloat(0.1).toString(2);

=> "0.0001100110011001100110011001100110011001100110011001101"

//二进制转十进制

parseInt(1100100,2)

=> 100

//以指定的精度返回该数值对象的字符串表示

(0.1 + 0.2).toPrecision(21)

=> "0.300000000000000044409"

(0.3).toPrecision(21)

=> "0.299999999999999988898"

参考

whyis0.1+0.2notequalto0.3inmostprogramminglanguages

IEEE-754标准与浮点数运算

Precision（精度）

（整数部分“除以二反序取余”）如：25
25/2 12......1
12/2 6......0
6/2 3......0
3/2 1......1
1/2 0......1
得10011
 25=（11001）<-二进制
（小数部分“乘二正序取整”）如：0.75
 0.75*2=1.50 整数部分为1
（取小数0.50）0.50*2=1.00 整数部分为1
（取小数0.00）计算结束
得11
0.75=（0.11)<-二进制