冒泡排序

以下：动图来源与五分钟学算法公众号，图片来自于《漫画算法》

讲解：

从动画可已看出，冒泡排序的思想，我们要把相邻的元素两两比较，根据大小来交换元素的位置。

代码：

原始版本

/**
 * 最原始的冒泡排序代码
 *
 * @param array
 */
public static void baseBubbleSore(int[] array) {
    for (int i = 0; i < array.length; i++) {
        for (int j = 0; j < array.length - i - 1; j++) {
            if (array[j] > array[j + 1]) {
                int temp = array[j];
                array[j] = array[j + 1];
                array[j + 1] = temp;
            }
        }
    }
}

优化版本

例如数列：{5，8，6，3，9，2，1，7}，执行第6、7、8轮的情况如下；

    很明显可以看出，自从经过第六轮排序，整个数列已然是有序的了。可是我们的排序算法仍然“兢兢业业”地继续执行第七轮、第八轮。

利用布尔变量isSorted作为标记。如果在本轮排序中，元素有交换，则说明数列无序；如果没有元素交换，说明数列已然有序，直接跳出大循环

代码：

/**
 * 进阶版本1： 对于已经有序的，则做出标记，不需要再进行排序比较。
 *
 * @param array
 */
public static void advancedBubbleSore1(int array[]) {
    for (int i = 0; i < array.length; i++) {
        // 有序的标记，每一轮的初始值都为true
        Boolean isSorted = true;
        for (int j = 0; j < array.length - i - 1; j++) {
            if (array[j] > array[j + 1]) {
                int temp = array[j];
                array[j] = array[j + 1];
                array[j + 1] = temp;
                isSorted = false;
            }

        }
        // 表示上一轮没有元素交换，则已经有序
        if (isSorted) {
            // 有序，则直接跳出循环
            break;
        }
    }
}

   还可以继续优化，例如数列：{3, 4, 2, 1, 5, 6, 7, 8}，这个数列的特点是前半部分（3，4，2，1）无序，后半部分（5，6，7，8）升序，并且后半部分的元素已经是数列最大值。

第一轮

元素3和4比较，发现3小于4，所以位置不变。

元素4和2比较，发现4大于2，所以4和2交换。

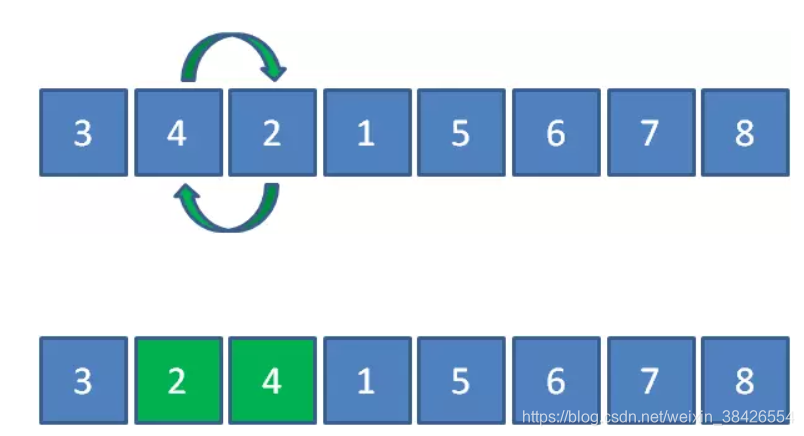
元素4和1比较，发现4大于1，所以4和1交换。

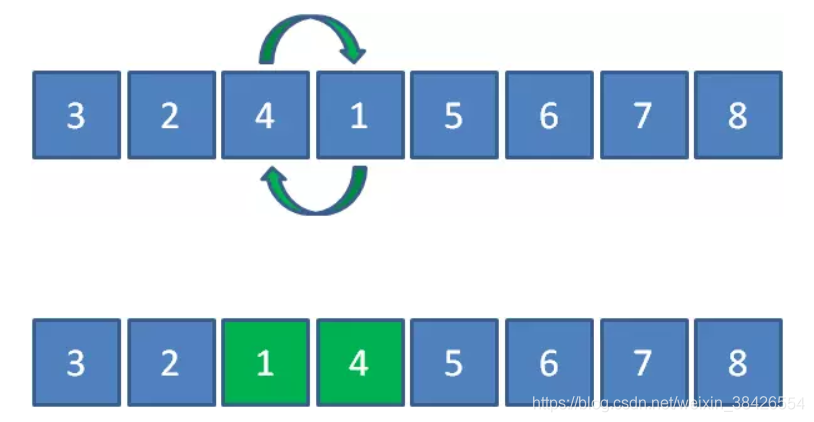
元素4和5比较，发现4小于5，所以位置不变。

元素5和6比较，发现5小于6，所以位置不变。

元素6和7比较，发现6小于7，所以位置不变。

元素7和8比较，发现7小于8，所以位置不变。

第一轮结束，数列有序区包含一个元素：

第二轮

 

元素3和2比较，发现3大于2，所以3和2交换

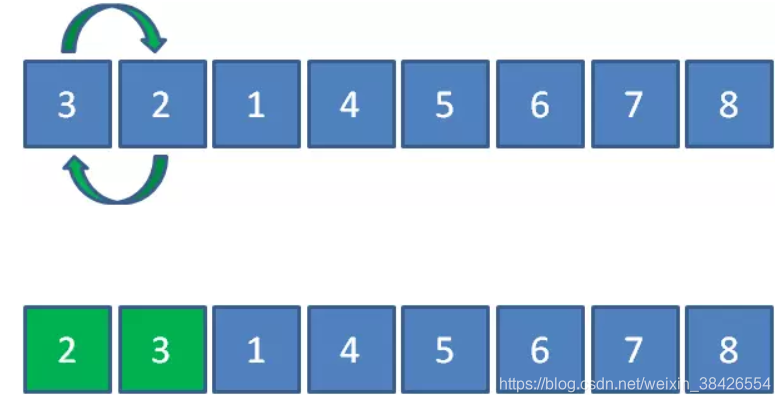
元素3和1比较，发现3大于1，所以3和1交换。

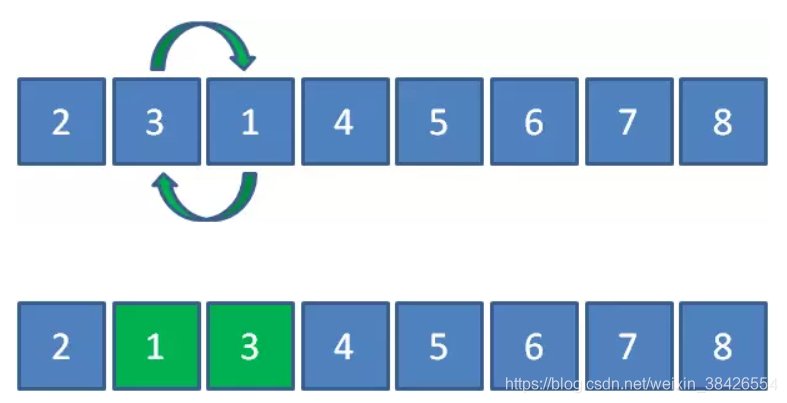
元素3和4比较，发现3小于4，所以位置不变。

元素4和5比较，发现4小于5，所以位置不变。

元素5和6比较，发现5小于6，所以位置不变。

元素6和7比较，发现6小于7，所以位置不变。

元素7和8比较，发现7小于8，所以位置不变。

第二轮结束，数列有序区包含一个元素：

按照现有的逻辑，有序区的长度和排序的轮数是相等的。比如第一轮排序过后的有序区长度是1，第二轮排序过后的有序区长度是2 ......

 

实际上，数列真正的有序区可能会大于这个长度，比如例子中仅仅第二轮，后面5个元素实际都已经属于有序区。因此后面的许多次元素比较是没有意义的。

 

如何避免这种情况呢？我们可以在每一轮排序的最后，记录下最后一次元素交换的位置，那个位置也就是无序数列的边界，再往后就是有序区了

/**
 * 进阶版本2： 对于数组后面的有序数列，在每一轮排序后，记录下来最后一次原始交换的位置，该位置即为无序数列的边界，再往后就是有序区。
 *          例如数列： {3, 2, 1, 4, 5, 6, 7, 8}
 *
 * @param array
 */
public static void advancedBubbleSore2(int array[]) {
    for (int i = 0; i < array.length; i++) {
        // 有序的标记，每一轮的初始值都为true
        Boolean isSorted = true;
        // 无序数列的边界，每次比较只需要比较到这里即可
        int soretBorder = array.length - 1;
        for (int j = 0; j < soretBorder; j++) {
            if (array[j] > array[j + 1]) {
                int temp = array[j];
                array[j] = array[j + 1];
                array[j + 1] = temp;
                // 因为有元素交换，所有不是有序的，标记为false
                isSorted = false;
                // 把无序数列的边界更新为最后一次交换元素的位置
                soretBorder = j;
            }
        }
        if (isSorted) {
            // 有序，则直接跳出循环
            break;
        }
    }
}

 

鸡尾酒版本

数列{2, 3, 4, 5, 6, 7, 8, 1}

鸡尾酒排序的元素比较和交换过程是双向的。

第一轮（和冒泡排序一样，8和1交换）

 

第二轮

 

此时开始不一样了，我们反过来从右往左比较和交换：

 

8已经处于有序区，我们忽略掉8，让1和7比较。元素1小于7，所以1和7交换位置：

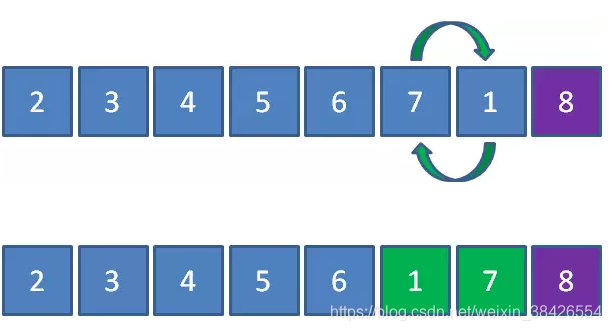
接下来1和6比较，元素1小于6，所以1和6交换位置：

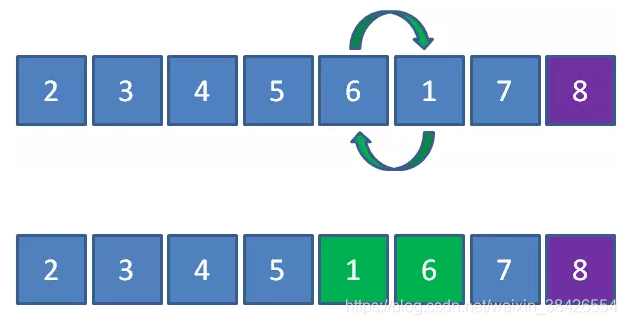
接下来1和5比较，元素1小于5，所以1和5交换位置：

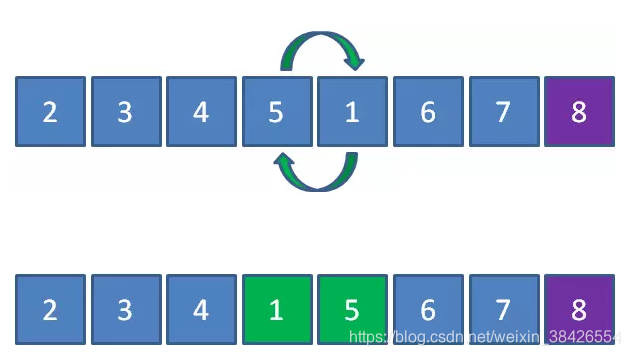
接下来1和4交换，1和3交换，1和2交换，最终成为了下面的结果：

第三轮（虽然已经有序，但是流程并没有结束）

 

鸡尾酒排序的第三轮，需要重新从左向右比较和交换：

1和2比较，位置不变；2和3比较，位置不变；3和4比较，位置不变......6和7比较，位置不变。

没有元素位置交换，证明已经有序，排序结束。

这就是鸡尾酒排序的思路。排序过程就像钟摆一样，第一轮从左到右，第二轮从右到左，第三轮再从左到右......

 

优缺点：能够在特定条件下，减少排序的回合数；而缺点也很明显，就是代码量几乎扩大一倍；

代码：

/**
 *  鸡尾酒版本
 * @param array
 */
public static void sort(int array[])
{
    int tmp  = 0;
   // 因为奇偶来回循环，所以这里外循环只要循环一半长度即可数组
    for(int i=0; i < array.length/2; i++)
    {
        //有序标记，每一轮的初始是true
        boolean isSorted = true;
        //奇数轮，从左向右比较和交换
        for(int j=i; j<array.length-i-1; j++)
        {
            if(array[j] > array[j+1])
            {
                tmp = array[j];
                array[j] = array[j+1];
                array[j+1] = tmp;
                //有元素交换，所以不是有序，标记变为false
                isSorted = false;
            }
        }
        if(isSorted){
            break;
        }

        //偶数轮之前，重新标记为true
        isSorted = true;
        //偶数轮，从右向左比较和交换
        for(int j=array.length-i-1; j>i; j--)
        {
            if(array[j] < array[j-1])
            {
                tmp = array[j];
                array[j] = array[j-1];
                array[j-1] = tmp;
                //有元素交换，所以不是有序，标记变为false
                isSorted = false;
            }
        }
        if(isSorted){
            break;
        }
    }
}