CART决策树Python代码详细实现

CART决策树Python代码实现

CART决策树：使用”基尼指数“来选择划分特征。数据集的纯度可用基尼值(Gini)来度量。Gini(D)反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率，Gini值越小，则数据集的纯度越高。

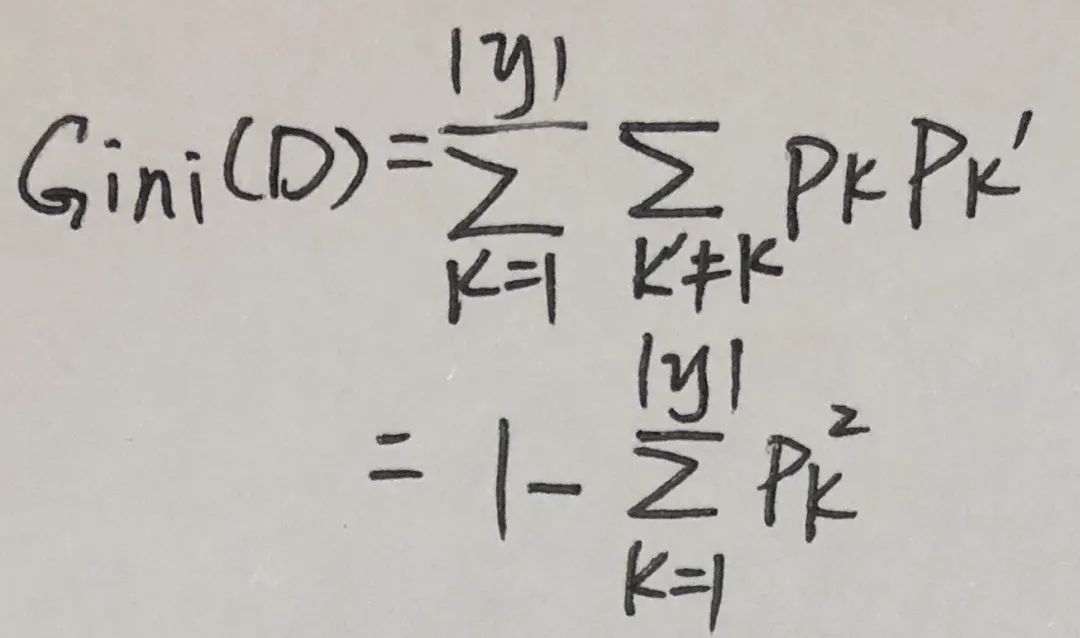
特征的“基尼指数”(Gini index)定义如下，选择使得划分后基尼指数最小的特征作为最优划分特征。

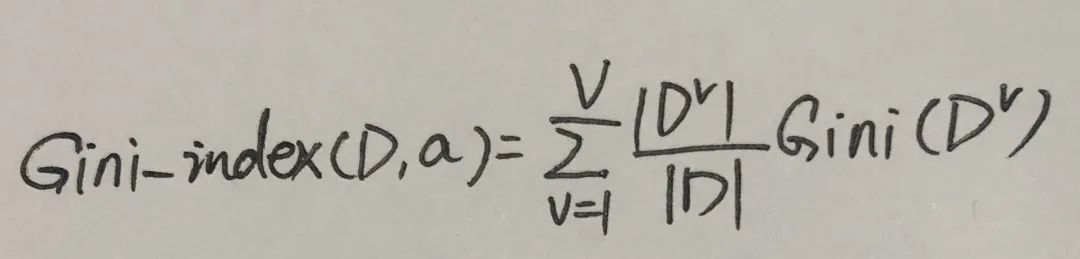
计算每个特征的基尼指数前，先计算下该节点的基尼值，若基尼值为0，则表示该节点下的数据集已完全分类。

接下来让我们大致复习一下Gini指数的计算：

根节点包含D中所有数据，数据总数为17，可用特征{色泽，根蒂，敲声，纹理，脐部，触感}：

★特征“色泽”：

1. 青绿：{1，4，6，10，13，17}，数据总计：6，正例p1= 3/6，反例p2= 3/6
Gin(青绿)=1−(3/6×3/6+3/6×3/6)=0.5

2. 乌黑：{2，3，7，8，9，15}，数据总计：6，正例p1= 4/6，反例p2= 2/6
Gini(乌黑)=1−(4/6×4/6+2/6×2/6)=0.444

3. 浅白：{5，11，12，14，16}，数据总计：5，正例p1= 1/5，反例p2= 4/5
Gini(浅白)=1−(1/5×1/5+4/5×4/5)=0.32