[Luogu 3902]Increasing

最新推荐文章于 2025-03-04 22:58:40 发布

weixin_38168081

最新推荐文章于 2025-03-04 22:58:40 发布

阅读量58

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/NaVi-Awson/p/7351616.html

本文介绍了一种求解最长不下降子序列的高效算法，通过预处理原数列并利用二分查找优化，实现快速求解。适用于大规模数据处理，如10^5级别的数据规模。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Description

Input

Output

Sample Input

3
1 3 2

Sample Output

HINT

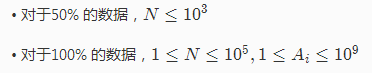
题解

由于题目要求我们求严格递增的数列，即：

$$A[i]>A[i-1],1<i<=N$$

我们不妨令B[i]=A[i]-i，那么我们容易得到

$$B[i]>=B[i-1],1<i<=N$$

两式是等价的。

那么我们可以将原数列处理一下，我们只需要求出$B[i]$的最长不下降子序列，把不在序列中的那些数$B[i]$都改成符合条件的数（比如说和左边最近一个在最长不下降子序列中的$B[j]$相等）就能满足题意了。

当然，我们并不需要求出具体的修改方案，我们只需要求出最长不下降的长度$K$，输出$N-K$即可。

注意：

由于数据为$10^5$显然我们要用二分优化求最长不下降子序列长度。同时由于减去了$i$，我们需要将数组初始化为极小值。

 1 #include<map>
 2 #include<set>
 3 #include<ctime>
 4 #include<cmath>
 5 #include<queue>
 6 #include<stack>
 7 #include<cstdio>
 8 #include<string>
 9 #include<vector>
10 #include<cstdlib>
11 #include<cstring>
12 #include<iostream>
13 #include<algorithm>
14 #define LL long long
15 #define RE register
16 #define IL inline
17 using namespace std;
18 const int N=1e5;
19 
20 int n,x;
21 int f[N+5],maxn;
22 
23 IL int Dev(int x)
24 {
25     int l=0,r=maxn,mid,ans;
26     while(l<=r)
27     {
28         mid=(l+r)>>1;
29         if (f[mid]<=x) ans=mid,l=mid+1;
30         else r=mid-1;
31     }
32     return ans;
33 }
34 IL int Min(int a,int b) {return a<b ? a:b;}
35 
36 int main()
37 {
38     memset(f,128,sizeof(f));
39     scanf("%d",&n);
40     for (RE int i=1;i<=n;i++)
41     {
42         scanf("%d",&x);
43         x-=i;
44         int tmp=Dev(x);
45         if (tmp==maxn) f[++maxn]=x;
46         else f[tmp+1]=Min(f[tmp+1],x);
47     }
48     printf("%d\n",n-maxn);
49     return 0;
50 }