高精度a+b

最新推荐文章于 2022-04-05 12:56:14 发布

weixin_38166852

最新推荐文章于 2022-04-05 12:56:14 发布

阅读量573

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/zxjhaha/p/11309539.html

本文详细介绍了一种处理高精度加法的算法实现，通过使用数组模拟竖式计算过程，解决longlong等基本数据类型无法处理的大数运算问题。文章提供了具体的C++代码示例，包括字符串输入转换、倒序存储、进位处理及结果输出等关键步骤。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

所谓“高精度”，就是两个几十甚至几百位的两个数进行四则运算。这时候long long也远远不够，所以我们要另辟蹊径——用数组模拟竖式计算。

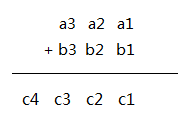
注：网图，https://i-blog.csdnimg.cn/blog_migrate/d556ce69f092e7bb60ab9a42cb10d5e3.png

我们用两个字符串a[505],b[505]用来输入。紧接着，定义两个int数组ans1[505],ans2[505]。把a,b倒过来(因为竖式从低位到高位算)且变成int类型存在ans1,ans2中。最后定义一个int类型的ans[505]，ans[i] 存ans1[i]+ans2[i]。最后逆向输出即可。代码如下。

#include <bits/stdc++.h>
using namespace std;
char a[505],b[505];
int ans[505],ans1[505],ans2[505];
int main()
{
	cin>>a>>b;
	int la=strlen(a); //求a的长度 。 
	int lb=strlen(b); //求b的长度。 
	for(int i=0;i<la;i++) ans1[i]=a[la-i-1]-'0'; //把a倒过来且变成int存储 。 
	for(int i=0;i<lb;i++) ans2[i]=b[lb-i-1]-'0'; //把b倒过来且变成int存储 。 
	int jw=0; //有可能出现进位，所以用jw记录 
	int maxl=max(la,lb); //若出现ans1,ans2长度不同，则取长的加数长度。因为定义在全局变量所以多余位为0。 
	for(int i=0;i<maxl;i++)
	{
		ans[i]=(ans1[i]+ans2[i]+jw)%10; //相加，若有进位%10可以保证此为为一位数。 
		jw=(ans1[i]+ans2[i]+jw)/10; //若相加大于0，则jw为1。否则为0. 
	}
	if(jw==1) cout<<1; //若最后有进位，则输出1。如：9+2=11,先输出1。 
	for(int i=maxl-1;i>=0;i--) cout<<ans[i]; //逆向输出。 
	return 0;
}

转载于:https://www.cnblogs.com/zxjhaha/p/11309539.html