Lecture 1 – Introduction and Word Vectors(19winter)

1. How do we represent the meaning of a word?
The first and arguably most important common denominator across all NLP tasks is how we represent words as input to any of our models. Much of the earlier NLP work that we will not cover treats words as atomic symbols. To perform well on most NLP tasks we first need to have some notion of similarity and difference between words. With word vectors, we can quite easily encode this ability in the vectors themselves (using distance measures such as Jaccard, Cosine, Euclidean, etc).

1.1 How do we have usable meaning in a computer?
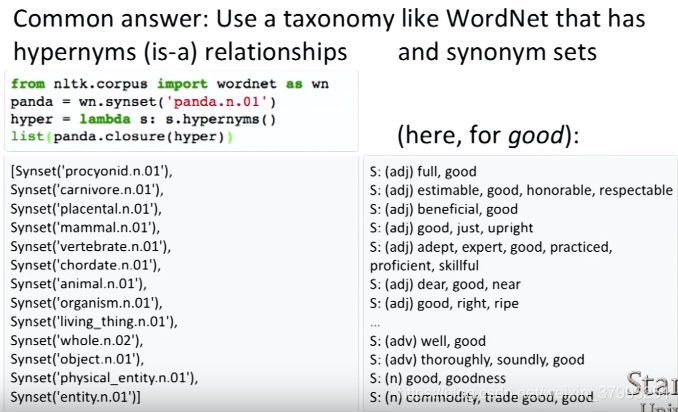
1.2 Problem with this discrete representation

one-hot vector
So let’s dive into our first word vector and arguably the most simple, the one-hot vector: Represent every word as an ![]() vector with all 0s and one 1 at the index of that word in the sorted english language. In this notation,
vector with all 0s and one 1 at the index of that word in the sorted english language. In this notation, ![]() is the size of our vocabulary. Word vectors in this type of encoding would appear as the following:
is the size of our vocabulary. Word vectors in this type of encoding would appear as the following:
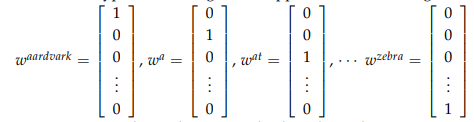
We represent each word as a completely independent entity. As we previously discussed, this word representation does not give us directly any notion of similarity. For instance,
![]()
So maybe we can try to reduce the size of this space from ![]() to something smaller and thus find a subspace that encodes the relationships between words.
to something smaller and thus find a subspace that encodes the relationships between words.

Problems with word as discrete symbols

1.3 Distributional similarity based representations

1.4 Word meaning is defined in terms of vectors

2. word2vec
There are an estimated 13 million tokens for the English language but are they all completely unrelated? Feline to cat, hotel to motel? I think not. Thus, we want to encode word tokens each into some vector that represents a point in some sort of "word" space. This is paramount for a number of reasons but the most intuitive reason is that perhaps there actually exists some N-dimensional space (such that N 13 million) that is sufficient to encode all semantics of our language. Each dimension would encode some meaning that we transfer using speech. For instance, semantic dimensions might indicate tense (past vs. present vs. future), count (singular vs. plural), and gender (masculine vs. feminine).
2.1 Basic idea of learning neural network word embeddings

2.2 Directly learning low-dimensional word vectors

Main idea of word2vec

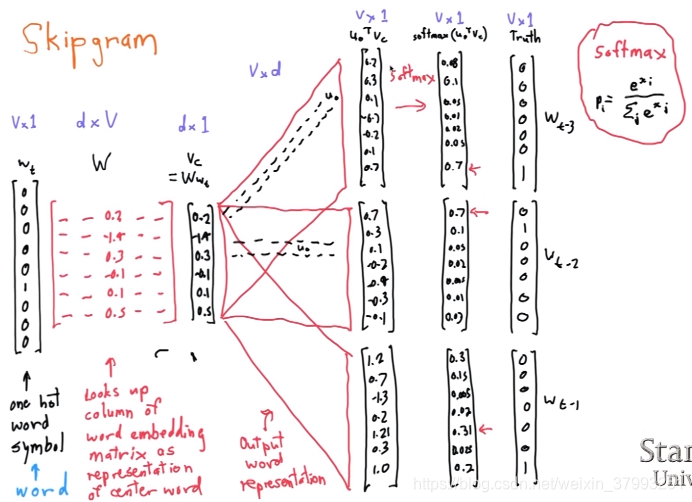
Skip-gram prediction
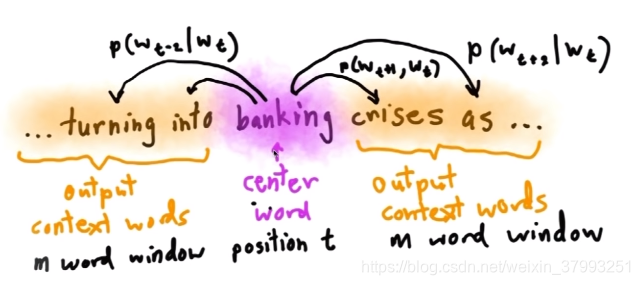
Skip-gram



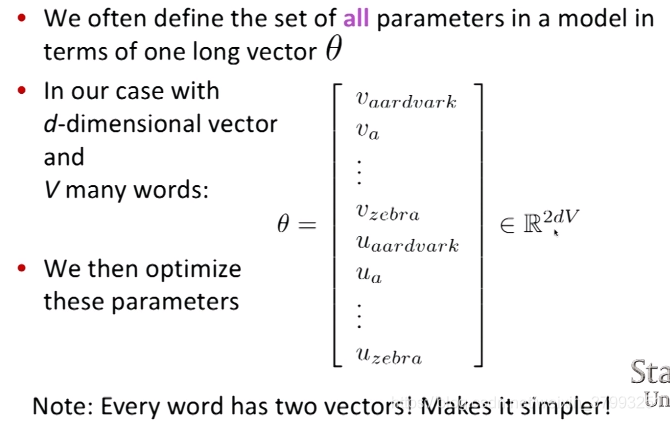
Details of word2vec

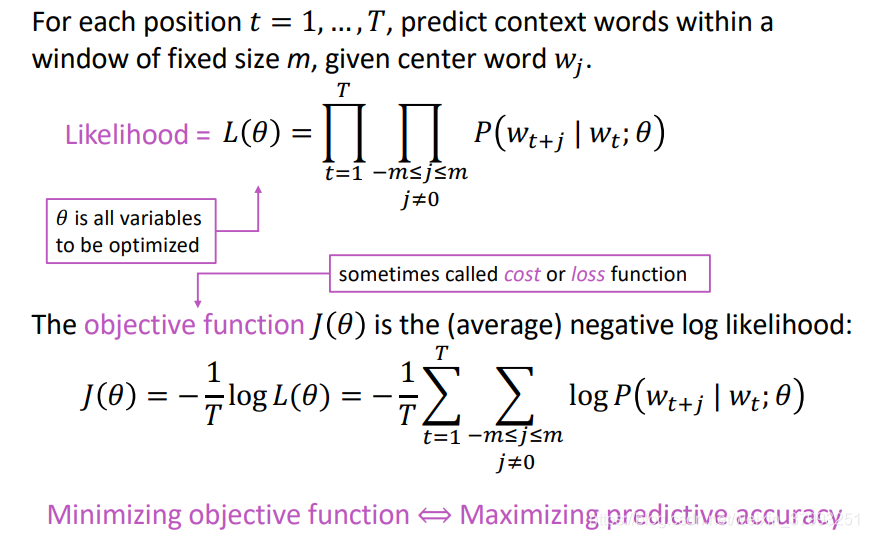
The objective function - details


dot products
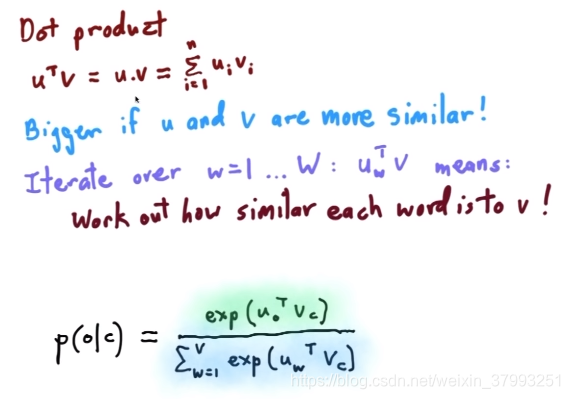
softmax
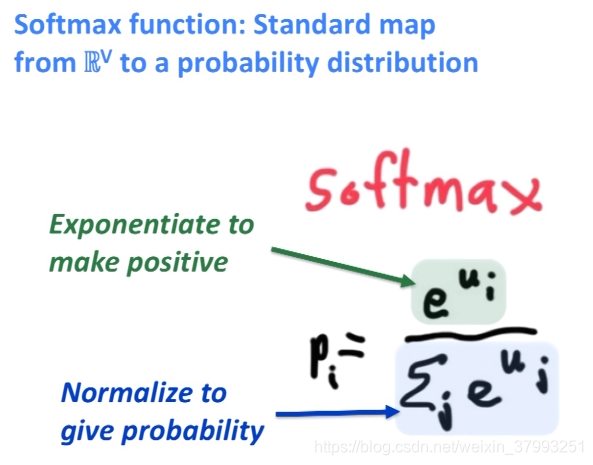
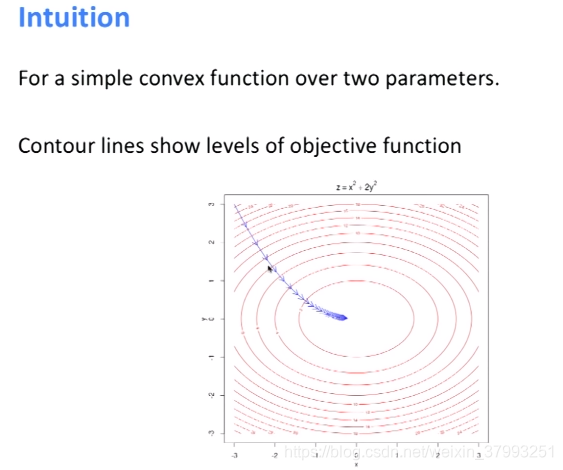
To train the model: Compute all vector gradients
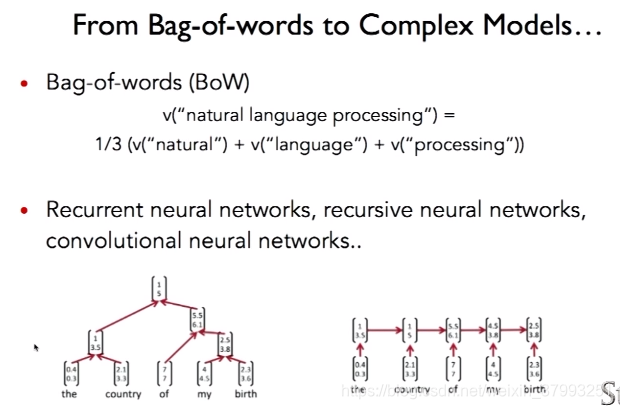
3. CS224N Research Highlight




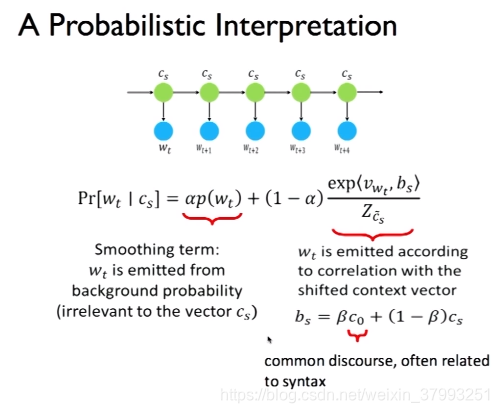
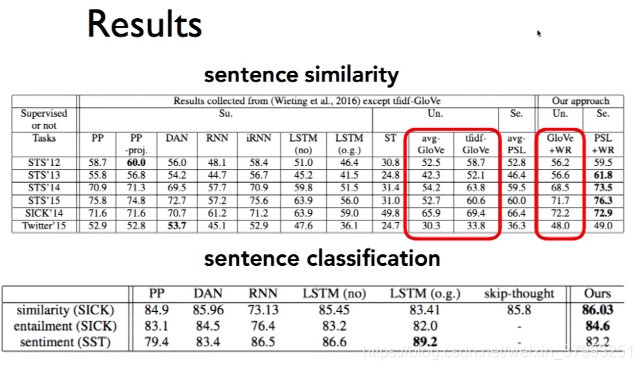
4. object function gradient

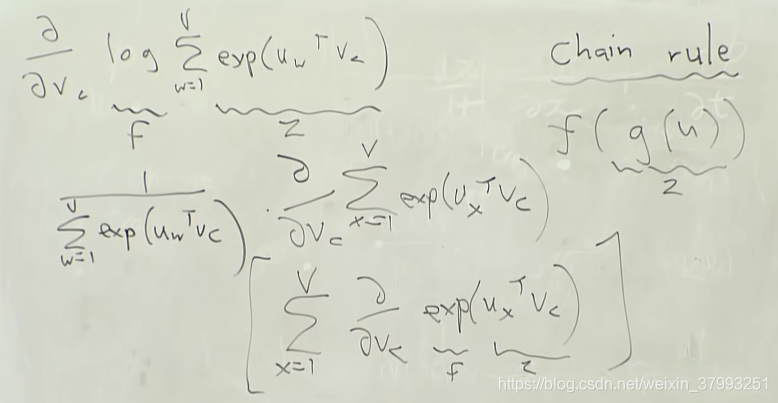
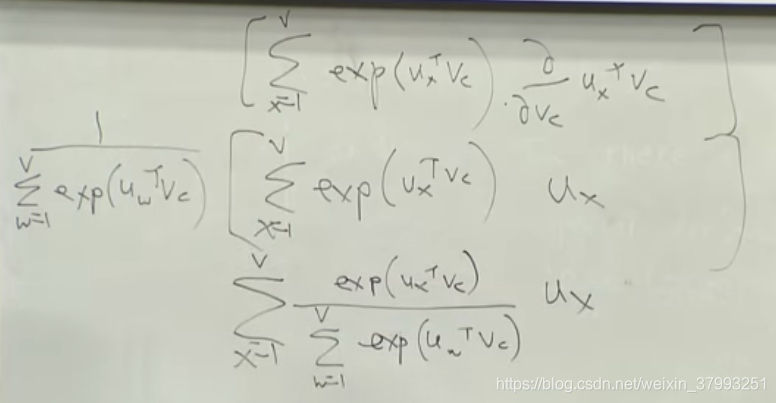




Gensim word vector visualization
import numpy as np
# Get the interactive Tools for Matplotlib
%matplotlib notebook
import matplotlib.pyplot as plt
plt.style.use('ggplot')
from sklearn.decomposition import PCA
from gensim.test.utils import datapath, get_tmpfile
from gensim.models import KeyedVectors
from gensim.scripts.glove2word2vec import glove2word2vecFor looking at word vectors, I'll use Gensim. We also use it in hw1 for word vectors. Gensim isn't really a deep learning package. It's a package for for word and text similarity modeling, which started with (LDA-style) topic models and grew into SVD and neural word representations. But its efficient and scalable, and quite widely used.
Our homegrown Stanford offering is GloVe word vectors. Gensim doesn't give them first class support, but allows you to convert a file of GloVe vectors into word2vec format. You can download the GloVe vectors from the Glove page. They're inside this zip file
(I use the 100d vectors below as a mix between speed and smallness vs. quality. If you try out the 50d vectors, they basically work for similarity but clearly aren't as good for analogy problems. If you load the 300d vectors, they're even better than the 100d vectors.)
glove_file = datapath('G:/Glove/glove.6B.100d.txt')
word2vec_glove_file = get_tmpfile("glove.6B.100d.word2vec.txt")
glove2word2vec(glove_file, word2vec_glove_file)(400000, 100)
model = KeyedVectors.load_word2vec_format(word2vec_glove_file)model.most_similar('obama')
[('barack', 0.937216579914093),
('bush', 0.927285373210907),
('clinton', 0.8960003852844238),
('mccain', 0.8875633478164673),
('gore', 0.8000321388244629),
('hillary', 0.7933663129806519),
('dole', 0.7851964235305786),
('rodham', 0.751889705657959),
('romney', 0.7488929629325867),
('kerry', 0.7472623586654663)]
model.most_similar('banana')
[('coconut', 0.7097253799438477),
('mango', 0.7054824233055115),
('bananas', 0.6887733936309814),
('potato', 0.6629636287689209),
('pineapple', 0.6534532904624939),
('fruit', 0.6519855260848999),
('peanut', 0.6420576572418213),
('pecan', 0.6349173188209534),
('cashew', 0.6294420957565308),
('papaya', 0.6246591210365295)]
model.most_similar(negative='banana')
[('keyrates', 0.7173938751220703),
('sungrebe', 0.7119239568710327),
('þórður', 0.7067720890045166),
('zety', 0.7056615352630615),
('23aou94', 0.6959497928619385),
('___________________________________________________________',
0.694915235042572),
('elymians', 0.6945434212684631),
('camarina', 0.6927202939987183),
('ryryryryryry', 0.6905653476715088),
('maurilio', 0.6865653395652771)]
result = model.most_similar(positive=['woman', 'king'], negative=['man'])
print("{}: {:.4f}".format(*result[0]))queen: 0.7699
def analogy(x1, x2, y1):
result = model.most_similar(positive=[y1, x2], negative=[x1])
return result[0][0]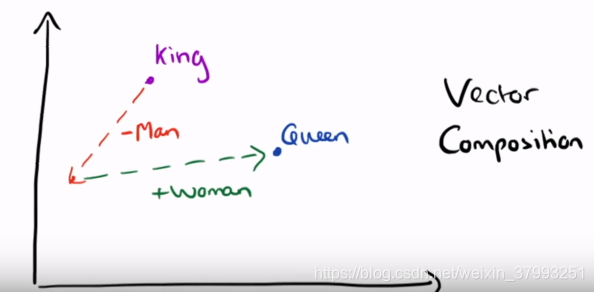
analogy('japan', 'japanese', 'australia')'australian'
analogy('japan', 'japanese', 'china')analogy('australia', 'beer', 'france')'champagne'
analogy('australia', 'beer', 'mexico')'tequila'
analogy('obama', 'clinton', 'reagan')'nixon'
print(model.doesnt_match("breakfast cereal dinner lunch".split()))cereal
def display_pca_scatterplot(model, words=None, sample=0):
if words == None:
if sample > 0:
words = np.random.choice(list(model.vocab.keys()), sample)
else:
words = [ word for word in model.vocab ]
word_vectors = np.array([model[w] for w in words])
twodim = PCA().fit_transform(word_vectors)[:,:2]
plt.figure(figsize=(6,6))
plt.scatter(twodim[:,0], twodim[:,1], edgecolors='k', c='r')
for word, (x,y) in zip(words, twodim):
plt.text(x+0.05, y+0.05, word)display_pca_scatterplot(model,
['coffee', 'tea', 'beer', 'wine', 'brandy', 'rum', 'champagne', 'water',
'spaghetti', 'borscht', 'hamburger', 'pizza', 'falafel', 'sushi', 'meatballs',
'dog', 'horse', 'cat', 'monkey', 'parrot', 'koala', 'lizard',
'frog', 'toad', 'monkey', 'ape', 'kangaroo', 'wombat', 'wolf',
'france', 'germany', 'hungary', 'luxembourg', 'australia', 'fiji', 'china',
'homework', 'assignment', 'problem', 'exam', 'test', 'class',
'school', 'college', 'university', 'institute'])
display_pca_scatterplot(model, sample=300)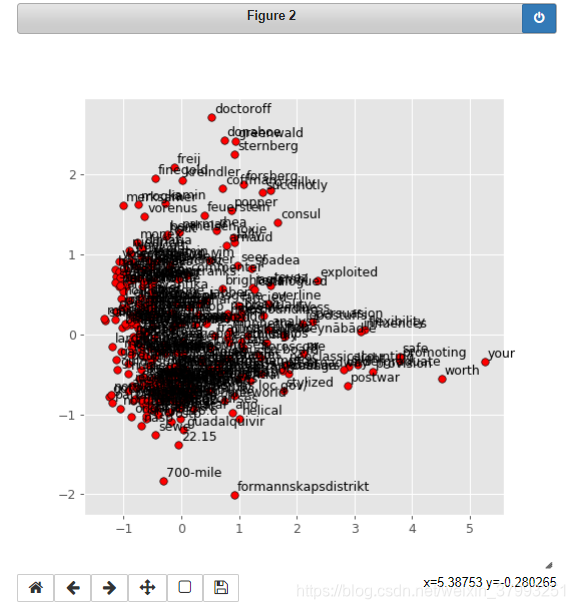







 本文介绍自然语言处理中词向量的基础概念,从简单的独热编码到分布假设下的词向量模型,重点讲解word2vec的工作原理及其应用。通过实例演示如何使用Gensim库加载并分析预训练的GloVe词向量。
本文介绍自然语言处理中词向量的基础概念,从简单的独热编码到分布假设下的词向量模型,重点讲解word2vec的工作原理及其应用。通过实例演示如何使用Gensim库加载并分析预训练的GloVe词向量。
















 1670
1670

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








