本文详细介绍了自定义神经网络的搭建过程及反向传播中的矩阵求导、激活函数求导与正则化求导等内容，通过实例帮助读者深入理解神经网络的工作原理。
事先声明一下，这篇博客的适用人群是对于卷积神经网络的基本结构和每个模块都基本了解的同学。当然，如果各位大神看到我这篇博客有什么不对的地方请大家积极指出哈，我一定好好改正，毕竟学习是一个不断改进的过程。
关键字： 神经网络、矩阵求导、链式法则、python
之前学习反向传播的时候，对于矩阵的求导、链式法则以及正则化的求导过程有些疑惑，我觉得是一个不错的机会来彻底搞清楚。
这里先开一个小差，我自己特别不喜欢推公式，因为推了几篇公式之后，编程实现就是这么几行，感觉超级不爽，。。。废话少说，下面开始进入主题。
下面是这篇博客的内容：
- 自定义神经网络搭建过程
- 反向传播过程中矩阵求导
- 反向传播过程中激活函数求导
- BONUS 反向传播过程中的正则化
- 总结
自定义神经网络搭建过程
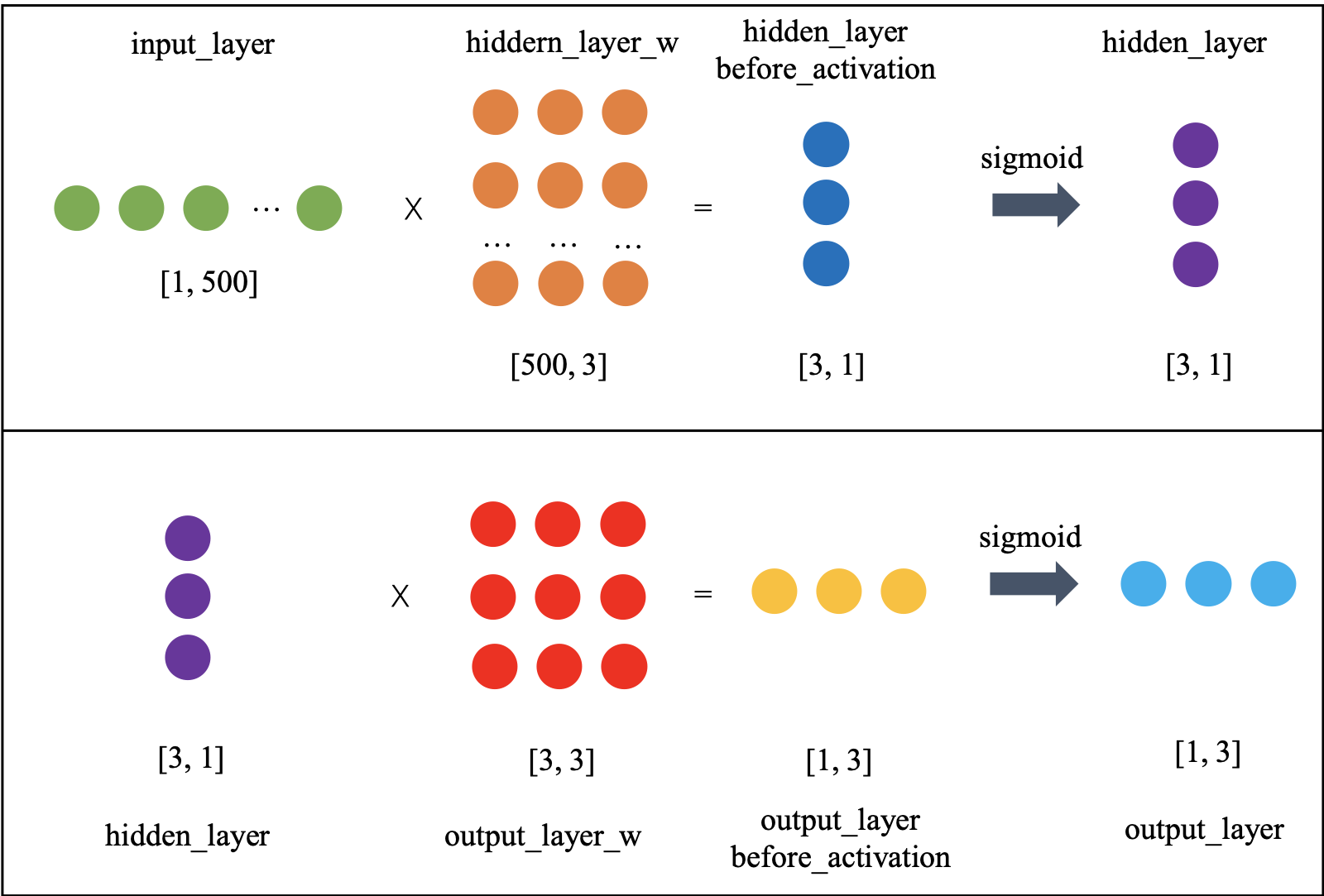
首先交代下整个神经网络的搭建过程。整个神经网络由三层组成：输入层，隐藏层和输出层组成。
-
输入层
输入的每条样本的维度为[1, 500], 每个样本的每一维都是从[-10,10]的区间内选取的随机整数。
-
隐藏层
隐藏层的维度为[500,3]，每一维都是[0,1]之间均匀分布的随机浮点数。隐藏层输出之后会经过sigmoid激活函数。
-
输出层
输出层的维度为[3,3]，每一维都是[0,1]之间均匀分布的随机浮点数。输出层输出之后会经过sigmoid激活函数。
-
标签
每个数据的标签是一个维度为[1,3]的向量，每个样本的每一维都是从[0, 1]的区间内选取的随机整数。因而从标签的形式可以看出，这个任务是一个多target分类任务。
-
损失函数
输出层与标签之间进行均方损失函数计算(这里说明的是，分类问题不应该是这么做，应该用分类问题特有的损失函数，这里只是为了方便起见)。
-
网络整体结构图
上述整个神经网络模型的示意图如下所示：
反向传播过程中矩阵求导
先从最简单的说起，就是最简单的affine layer（全连接层）的反向传播，在这一层中的前向传播如下公式,
x
x
x是这层的输入，
w
w
w是这层的参数，
b
b
b是这层的偏置,
o
u
t
out
out是这层的输入，
o
u
t
=
x
∗
w
+
b
out = x * w + b
out=x∗w+b
这里为了简便，省略了偏置项(
b
b
b)，下图展示了反向传播过程中的计算流程，这里展示的是输入层和隐藏层矩阵相乘之后的反向传播状态。
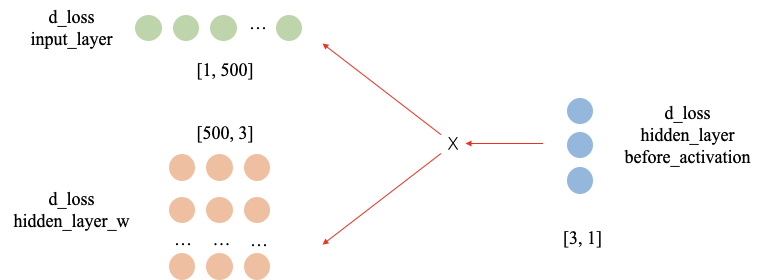
其中d_loss_input_layer代表的是输入层的梯度，d_loss_hidden_layer_w代表的是隐藏层权重矩阵的梯度，d_loss_hidden_layer_before_activation代表的是隐藏层输入到激活函数之前的结果的梯度。
根据矩阵求导的链式法则可得(其中
{
x
→
y
→
z
}
\{x\rightarrow y\rightarrow z\}
{x→y→z}代表的含义是由x推出y，再由y推出z，
×
\times
×代表的含义是矩阵相乘)，
∂
z
∂
x
=
(
∂
y
∂
x
)
T
×
∂
z
∂
y
{
x
→
y
→
z
}
\frac{\partial z}{\partial x}=(\frac{\partial y}{\partial x})^T\times \frac{\partial z}{\partial y} \ \ \ \ \{x\rightarrow y\rightarrow z\}
∂x∂z=(∂x∂y)T×∂y∂z {x→y→z}
可得如下公式，
∂
l
o
s
s
∂
i
n
p
u
t
_
l
a
y
e
r
=
(
∂
h
i
d
d
e
n
_
l
a
y
e
r
_
b
e
f
o
r
e
_
a
c
t
i
v
a
t
i
o
n
∂
i
n
p
u
t
_
l
a
y
e
r
)
T
×
∂
l
o
s
s
∂
h
i
d
d
e
n
_
l
a
y
e
r
_
b
e
f
o
r
e
_
a
c
t
i
v
a
t
i
o
n
∂
l
o
s
s
∂
h
i
d
d
e
n
_
l
a
y
e
r
_
w
=
(
∂
h
i
d
d
e
n
_
l
a
y
e
r
_
b
e
f
o
r
e
_
a
c
t
i
v
a
t
i
o
n
∂
h
i
d
d
e
n
_
l
a
y
e
r
_
w
)
T
×
∂
l
o
s
s
∂
h
i
d
d
e
n
_
l
a
y
e
r
_
b
e
f
o
r
e
_
a
c
t
i
v
a
t
i
o
n
\frac{\partial loss}{\partial input\_layer}=(\frac{\partial hidden\_layer\_before\_activation}{\partial input\_layer})^T\times\frac{\partial loss}{\partial hidden\_layer\_before\_activation} \\ \frac{\partial loss}{\partial hidden\_layer\_w }=(\frac{\partial hidden\_layer\_before\_activation}{\partial hidden\_layer\_w})^T\times\frac{\partial loss}{\partial hidden\_layer\_before\_activation}
∂input_layer∂loss=(∂input_layer∂hidden_layer_before_activation)T×∂hidden_layer_before_activation∂loss∂hidden_layer_w∂loss=(∂hidden_layer_w∂hidden_layer_before_activation)T×∂hidden_layer_before_activation∂loss
而反向传播过程中要解决的核心问题是权重矩阵的参数更新问题，因而这里只关注d_loss_hidden_layer_w的计算，又根据矩阵求导的法则，
∂
β
T
x
∂
x
=
β
\frac{\partial \beta ^Tx}{\partial x}=\beta
∂x∂βTx=β
可得
∂
h
i
d
d
e
n
_
l
a
y
e
r
_
b
e
f
o
r
e
_
a
c
t
i
v
a
t
i
o
n
∂
h
i
d
d
e
n
_
l
a
y
e
r
_
w
=
i
n
p
u
t
_
l
a
y
e
r
T
\frac{\partial hidden\_layer\_before\_activation}{\partial hidden\_layer\_w}=input\_layer^T
∂hidden_layer_w∂hidden_layer_before_activation=input_layerT
即
∂
l
o
s
s
∂
h
i
d
d
e
n
_
l
a
y
e
r
_
w
=
i
n
p
u
t
_
l
a
y
e
r
T
×
∂
l
o
s
s
∂
h
i
d
d
e
n
_
l
a
y
e
r
_
b
e
f
o
r
e
_
a
c
t
i
v
a
t
i
o
n
\frac{\partial loss}{\partial hidden\_layer\_w }=input\_layer^T\times\frac{\partial loss}{\partial hidden\_layer\_before\_activation}
∂hidden_layer_w∂loss=input_layerT×∂hidden_layer_before_activation∂loss
这样只需要知道
∂
l
o
s
s
∂
h
i
d
d
e
n
_
l
a
y
e
r
_
b
e
f
o
r
e
_
a
c
t
i
v
a
t
i
o
n
\frac{\partial loss}{\partial hidden\_layer\_before\_activation}
∂hidden_layer_before_activation∂loss，就能够将隐藏层的权重矩阵的梯度求解出来，而该结果又是通过链式法则的前端传递过来的，因而需要计算前面的结果，这里才能够知道，具体计算结果这里就不再赘述，因为这里重点讲的是矩阵求导的过程。
反向传播过程中激活函数求导
激活函数的意义是为神经网络的计算添加非线性，这样神经网络就能够拟合更加复杂的曲线，不过这不是本文的重点，大家有兴趣的可以参考其他博客。这里重点介绍的是激活函数再反向传播中是如何求导的，这里以sigmoid函数为例来详细介绍。首先给出的是该种情况下反向传播的过程示意图，其中d_sigmoid代表的是sigmoid函数的求导函数。
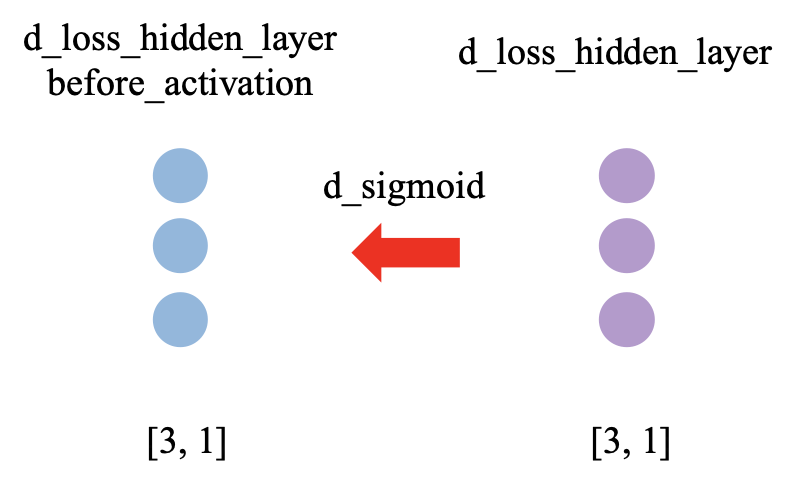
由于这里在前向计算时是逐位点乘的，因而这里不涉及矩阵求导，但是这里依然存在链式法则，因而计算公式如下，
∂
l
o
s
s
∂
h
i
d
d
e
n
_
l
a
y
e
r
_
b
e
f
o
r
e
_
a
c
t
i
v
a
t
i
o
n
=
d
_
s
i
g
m
o
i
d
(
h
i
d
d
e
n
_
l
a
y
e
r
_
b
e
f
o
r
e
_
a
c
t
i
v
a
t
i
o
n
)
∗
∂
l
o
s
s
∂
h
i
d
d
e
n
_
l
a
y
e
r
\frac{\partial loss}{\partial hidden\_layer\_before\_activation}= \\ d\_sigmoid(hidden\_layer\_before\_activation)*\frac{\partial loss}{\partial hidden\_layer}
∂hidden_layer_before_activation∂loss=d_sigmoid(hidden_layer_before_activation)∗∂hidden_layer∂loss
这里值得注意的是，上面公式中
∗
*
∗代表的是矩阵的逐位点乘，而不是矩阵相乘。
到此，反向传播过程中激活函数求导讲述完毕。上述过程的完整代码可以参考我的github repo， 每一步都是手工计算，过程中只利用了numpy函数库，个人认为可以较为清晰的解答简单神经网络前向和反向传播过程中的细节问题。大家如果有兴趣，可以一起维护这个repo~
BONUS 反向传播过程中的正则化
正则化的基本思想是通过限制参数的野蛮生长而诞生的技术，说白了就是抑制过拟合，让模型的泛化能力更强。具体的做法是在计算损失时加入了权重矩阵的正则项，这样如果权重矩阵每个元素的取值太大的话，会导致整体的损失变大，因而为了使损失变小，在学习过程中会抑制参数变得很大，这里所说的"很大"指的是绝对值很大或者平方项很大，分别对应了l1正则项和l2正则项。因而下文会讲述这两个正则项的求导过程以及两个正则化项在实际运用时对结果的影响。
-
l1正则项
反向传播的计算公式如下所示：
∂ l o s s ∂ w l 1 = { 1 i f w > 0 − 1 i f w < 0 \frac{\partial loss}{\partial w}_{l1}=\left\{\begin{matrix} 1 \ \ \ \ if \ w > 0\\ -1 \ \ if \ w < 0 \end{matrix}\right. ∂w∂lossl1={1 if w>0−1 if w<0 -
l2正则项
反向传播的计算公式如下所示：
∂ l o s s ∂ w l 2 = w \frac{\partial loss}{\partial w}_{l2}=w ∂w∂lossl2=w -
实际应用
将正则项运用到第一节所搭建的神经网络中，分别对比了不加正则项、l1正则项和l2正则项之间的训练和验证损失的差异，示意图如下所示：
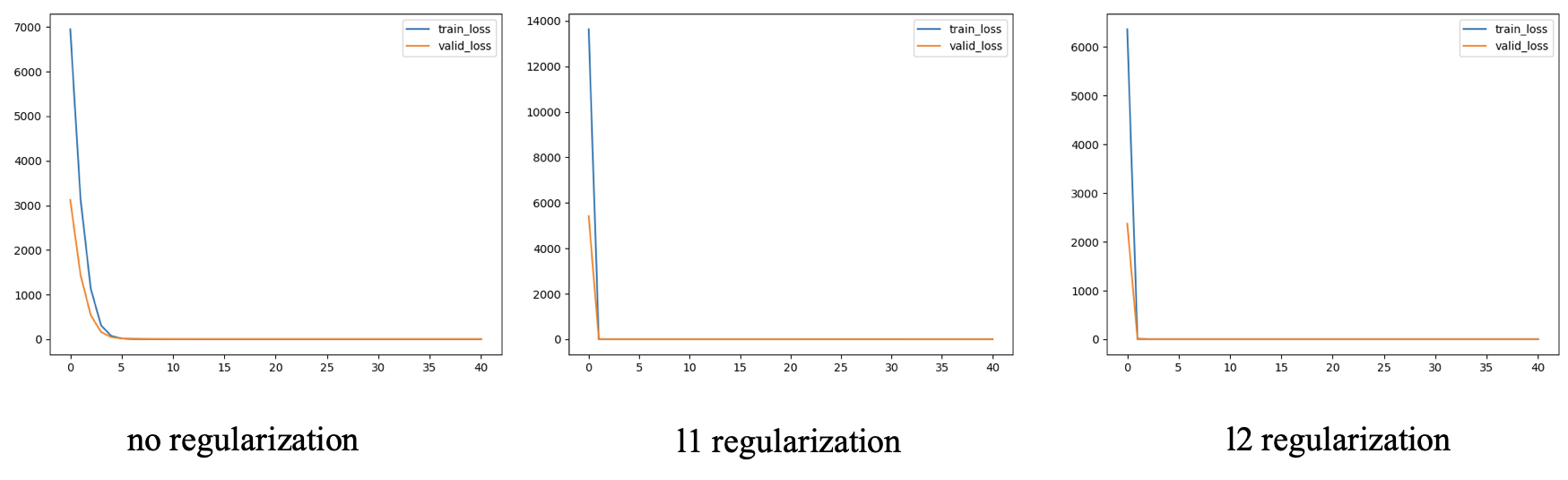
可以看出，添加了正则项之后，验证集能够更快地收敛，而对于数值特征，上述示意图显示的不是特别明显，这里截取了训练过程中训练loss和验证loss的数值结果，如下所示(到1600次迭代时基本已经收敛)，不加正则项：
iteration 1600, train loss: 0.3432821160251056, valid_loss: 2.5690724565021563l1正则项：
iteration 1600, train loss: 0.20726140239368068, valid_loss: 0.019843994548783522l2正则项：
iteration 1600, train loss: 1.09977712566086, valid_loss: 0.21506450810326314这里可以明显地看出，不加正则项收敛时，训练loss会很低，但是验证loss比较大，而l1和l2正好相反，经过添加正则项的操作之后，验证loss更低，这就能说明添加正则项确实比不添加正则项的效果要好。而在这里为何l1比l2的效果要好，目前楼主还没有想到一个比较好的答案，等大段时间了可以好好想一下，或者大家可以一起来想一下~
总结
手动实现神经网络，可以消除之前对神经网络反向传播计算的恐惧，并且对矩阵求导以及链式法则有了一个更加深刻的认识，希望以后能够在这个领域由更多的见解，也希望大家如果对该博客有什么异议，一定提出来，共同学习，共同提高~
扫一扫
3万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
