机器学习 - KNN、KD树、偏差 and 方差

（KNN 是一种分类算法，它没有学习的过程，而是直接计算出预测结果）

• KNN

  1. 算法步骤

     (1) 计算 被预测点 到所有“训练样本”的距离

     (2) 从中找出前 k 个距离最近的样本点

     (3) 根据分类决策规则决定（预测） 被预测点 的类别

  2. 距离度量

     使用不同的距离度量所确定的临近点可能是不同的。

     两点间距离计算：$L_p(x_i,x_j)=[{\sum }_{l=1}^m|x_i^{(l)}-x_j^{(l)}{|}^p{]}^{\frac{1}{p}}$，

     $i,j$ 表示第 $i,j$ 个样本，$k$ 为个样本第 $k$ 个特征。

     $p=1$ 时，$L_p$ 为曼哈顿距离；
     $p=2$ 时，$L_p$ 为欧氏距离。

  3. K 的选取

     $k$ 值可以用来描述 被预测点 的邻域的大小，其值的选取对结果影响很大。

     (1) $k$ 越小，近似误差越小，预测误差越大，对噪声越敏感，越容易过拟合；（只受周围少数样本影响，加入附近有噪声点，那就有可能被分为噪声点的类别，所以容易过拟合）

     (2) $k$ 越大，近似误差越大，预测误差越小，对噪声越不敏感，容易欠拟合。（受周围更多的样本点影响，因为噪声点较少所以不容易过拟合，但样本点多时容易欠拟合，可理解为“人多嘴杂”。假设 k=9，其中 5 个样本指向类别 1，4个样本指向类别 2，可能这个被分类样本的真实标签是 2，但此时因为 K 值变大，将离得稍远的但个数较多的类别 1 也包括进来，此时被分类样本就被错误分类。）

  4. 多数表决规则

     在距离 被预测点 最近的 k 个样本中，哪一类别的个数最多，则 被预测点属于哪一类。

  5. KNN 特点

     (1) 基于样本实例计算，而非训练；

     (2) 分类时开销大，属于消极学习方法；

     (3) 基于局部信息预测，对噪声敏感；

     (4) 可产生任意形状的决策边界，非简单线性；

     (5) 受值域较大的属性影响较大，应统一量纲，归一化。

  6. KD 树

     实现 KNN 算法时，主要考虑的问题是如何快速在训练数据中搜索，在高维特征空间以及大训练集时非常重要。通常 KNN 实现的方法是快速扫描，即暴力搜索，计算目标数据与所有训练数据的距离，这样计算非常耗费时间。

     为了提高效率，考虑使用特殊存储结构存储训练数据，以减少计算距离的次数，由此 KD 树诞生了。

     KD 树的 K 与 KNN 中的 K 是不同的，它指代 K 维空间。KD 树以建树为核心思想，建树的过程是通过对每一维度进行划分完成的。具体的：

     1）以包含所有训练数据的超矩形作为根节点，依次选择不同纬度，对于选出的维度标定切分点，以切分点将超矩形内的数据进行划分，小于切分点的数据归为左结点，大于切分点的数据归为右结点，并视为深度 1；

     2）深度增加，选择维度，标定切分点，划分为左右结点，重复进行，直至所有结点被划分完毕；

     3）对目标节点搜索最近邻。首先找到目标节点在 KD 树中所属的结点，而后并将与兄弟结点之间的距离 D^*设为当前最近距离，以目标节点为球心，D^* 为半径规定超球体。

     4）对父节点进行计算，比较父节点的父节点所表示的超矩形与超球体是否有交集，有交集则寻找父节点的兄弟结点，否则再向上寻找父节点。直至找到最近邻。

• 偏差与方差

  我们经常用过拟合、欠拟合来定性地描述模型是否很好的解决了特定的问题。从定量的角度来说，可以用模型的偏差（Bias）与方差（Variance）来描述模型的性能。

  1. 偏差

     偏差是指由所有采样得到的大小为 m 的训练数据集训练出所有模型的输出的 平均值（中心） 和真实标记之间的偏差。描述所有预测结果 整体 对真实标记的“偏离程度”，即所有预测分布的中心对真实标记分布的 偏离程度。可以衡量模型对数据集的学习程度。

     偏差通常是由于我们对学习算法做出了错误的假设所导致的。由偏差带来的误差通常在训练误差上就能体现出来。

     偏差越大，对数据集的拟合程度越差；偏差越小，拟合程度越好。

  2. 方差

     方差是指由所有采样得到的大小为 m 的训练数据集训练出的所有模型的输出的方差。描述所有预测结果对预测结果中心的 离散程度（聚集密度），可以衡量数据扰动对模型的影响程度。

     方差通常是由于模型的复杂度相对于训练样本数 m 过高导致的。由方差带来的误差通常体现在测试误差相对于训练误差的增量上。

     方差越大，对噪声越敏感，越容易过拟合；方差越小，与不容易过拟合。

  3. 图解

     我们使用射击的例子来进一步解释。假设一次射击就是一个模型对一个样本进行预测。射中靶心代表预测准确，越偏离靶心代表预测误差越大。

     我们通过 n 次采样得到 n 个大小为 m 的训练样本集合，训练处 n 个模型，对同一个样本进行预测，相当于我们进行了 n 次射击。

     具体对偏差与方差的理解可看图。
     
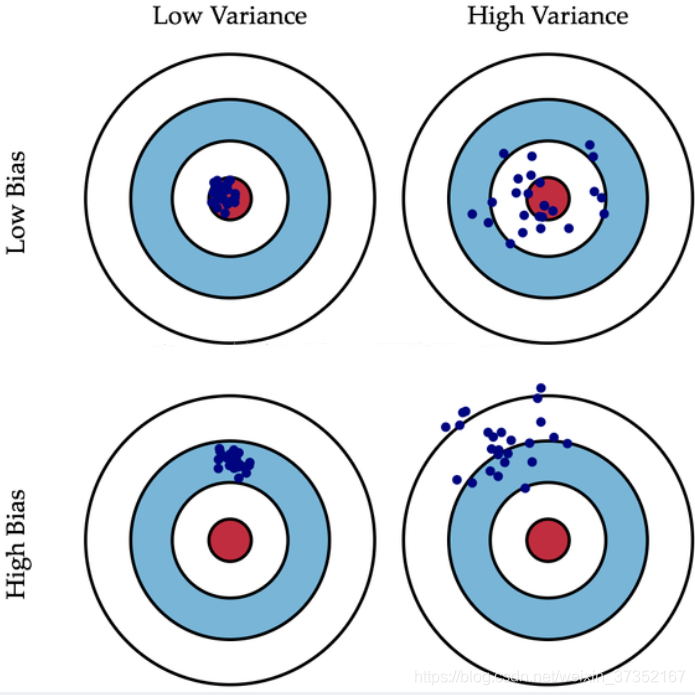
     （图片来自网络）
     
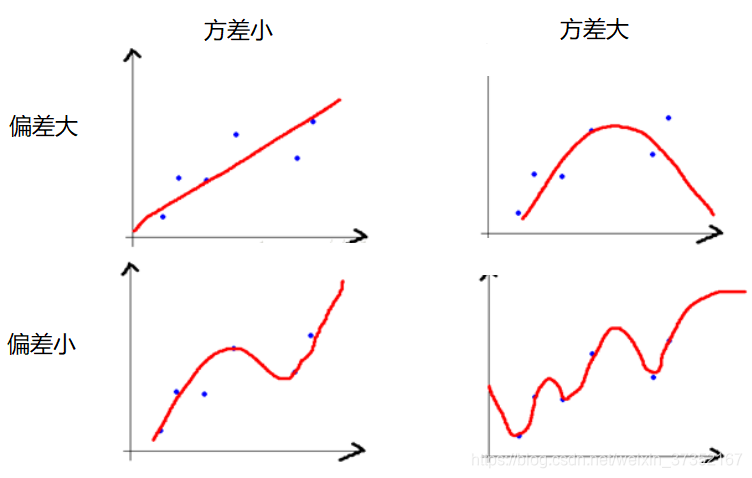
     （图片来自网络）