周志华 机器学习 Day20

嵌入式选择与L1正则化

嵌入式特征选择是将特征选择过程与学习器训练过程融为一体，两者在同一个优化过程中完成，即在学习器训练过程中自动地进行了特征选择。

给定数据集D=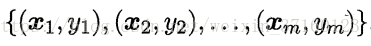，其中x∈R，y∈R。我们考虑最简单的线性回归模型，以平方误差为损失函数，则优化目标为

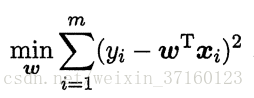
当样本特征很多，而样本数相对较少时，上式容易陷入过拟合。为了缓解过拟合问题，可对上式引入正则化项，若使用L2范数正则化。

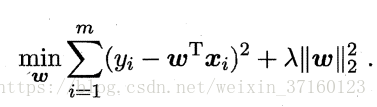
其中正则化参数λ>0。上式称为“岭回归”，通过引入L2范数正则化，确能显著降低过拟合的风险。

L1范数和L2范数正则化都有助于降低过拟合风险，但前者还会带来一个额外的好处：它比后者更易于获得“稀疏”解，即它求得的ω会有更少的非零分量。

稀疏表示与字典学习

不妨把数据集D考虑成一个矩阵，其每行对应于一个样本，每列对应于一个特征。特征选择所考虑的问题是特征具有“稀疏性”，即矩阵中许多列与当前学习任务无关，通过特征选择去除这些列，则学习器训练过程仅需在小的矩阵上进行，学习任务的难度可能有所降低，设计的计算和存储开销会减少，学得模型的可解释性也会提高。

一般的学习任务中（例如图像分类），我们需要学习出这样一个“字典”。为普通稠密表达的样本找到合适的字典，将样本转化为合适的稀疏表示形式，从而使学习任务得以简化，模型复杂度得以降低，通常称为“字典学习”，亦称“稀疏编码”。“字典学习”更侧重于学得字典过程，而“稀疏编码”则更侧重于对样本进行稀疏表达的过程。

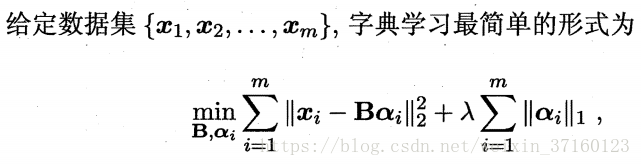
其中，B∈R（d*k）是字典矩阵，k称为字典的词汇量，通常由用户指定，ai∈Rk则是样本xi∈Rd的稀疏表示。