周志华 机器学习 Day8

我们以上图隐层到输出层的连接权whj为例推导：

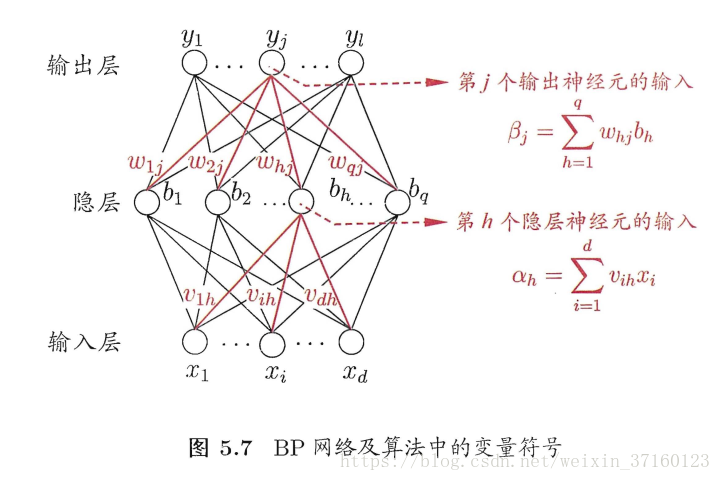
BP算法基于梯度下降策略，以目标的负梯度方向对参数进行调整，对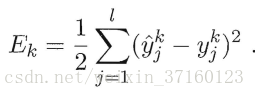的误差Ek，给定学习率η，有

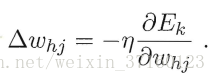
往下推导过程详看P103起

Sigmoid函数有一个很好的性质：f'(x)=f(x)(1-f(x))

一般地，我们把学习率η∈（0,1）设置成0.1，这样不会导致太大容易震荡，太小收敛速度过慢。

误差逆传播算法

一般来说，标准BP算法仅针对单个样例，参数更新非常频繁，而且对不同样例进行更新的效果可能出现“抵消”现象；因此，为了达到同样地累积误差极小点，标准BP算法需要进行多次的迭代。累积BP算法直接针对累积误差最小化，它在读取整个训练集D 一遍后才对参数进行更新，其参数更新的频率低得多。

有两种方法来防止BP网络的过拟合：（1）“早停”：将数据分成训练集和验证集，训练集用来计算梯度、更新连接权和阈值，验证集用来估计误差，若训练集误差降低但验证集误差升高，则停止训练，同时返回具有最小验证集误差的连接权和阈值。（2）“正则化”：在误差目标函数中增加一个用于描述网络复杂度的部分，例如连接权与阈值的平方和，仍令Ek表示第k个训练样例上的误差，wi表示连接权和阈值，则误差目标函数改变为

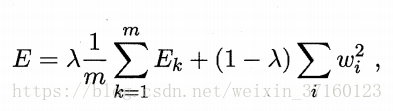
其中λ∈（0,1）用于对经验误差与网络复杂度这两项进行折中，常通过交叉验证法来估计。

全局最小和局部极小

神经网络的训练过程可看做一个参数寻优的过程，即在参数空间中，寻找一组最优参数使得误差E最小。

我们通常会谈到两种“最优”：“局部极小”和“全局最小”。

基于梯度的搜索是使用最为广泛的参数寻优方法，在此类方法中，我们从某些初始解出发?迭代寻找最优参数值.每次迭代中，我们先计算误差函数在当前点的梯度，然后根据梯度确定搜索方向。例如，由于负梯度方向是函数值下降最快的方向，因此梯度下降法就是沿着负梯度方向搜索最优解；若误差函数在当前点的梯度为零，则已达到局部极小，更新量为零，这意味着参数的迭代更新将在此停止。

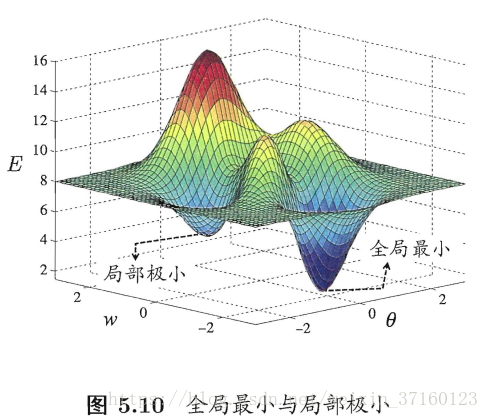
在现实任务中，人们常采用以下策略试图“跳出”局部极小，从而进一步接近全局最小。