最速降曲线问题

设 O, A是高度

不同，且不在同一铅垂线上的两定点，y

如果不计摩擦和空气阻力，一质点 m

在重力作用下从 O点沿一曲线降落至 。A(p,q) A点，问曲线呈何种形状时，质点降y

落的时间最短。

图 7-1 设曲线为 y =y(x) ，坐标如图 7

1，质点由 O点开始运动，它的速度 v与它的纵坐标有关系

式中， g是重力加速度。

在曲线上点 (x, y) 处，质点的运动速度为

式中， s表示曲线的弧长， t表示时间，于是

由于点 O, A的横坐标分别是 0, p，则质点 m从 O点运动到 A点所需时间为

 

(7.1.4))

这样，质点由 O点运动到 A点所需时间 t是 y(x)的函数，最速降线问题就是满足边界条件

y(0)= 0, y( p) = q

的所有连续函数 y(x)中，求出一个函数 y使泛函式（7.1.4）取最小值。

对泛函求极值的问题称为变分问题，使泛函取极值的函数称为变分问题的解，也称为极值函数。

在微分学中，求函数 y =y(x) 的极值是求自变量 x的值，当 x取这些值时， y取极 大（小）值、取极值的必要条件是dy/dx= 0 。下面我们仿照函数微分的概念来定义泛函的变分概念，进而导出泛函极值存在的必要条件。设 y, y0 是集合 C的元素，称δy = y − y0 为函数 y在 y0处的变分。

这里的δy是 x的函数，它与 ∆y的区别在于：变分 δy反映的是整个函数的改变，

而 ∆y表示的是同一个函数 y(x)因 x的不同值而产生的差异。在本书，我们总是假定 y(x)和 F(x, y, y′) 都是充分光滑的，且 y(x)在两个端点处固定，即 y(a) =y1, y(b) = y2 （7.1.5）

式中， y1, y2是两个常数。

考虑泛函

 

（7.1.6）当函数 y(x)有微小改变且变为 y(x) +δy(x) 时，利用

上式可推出

上式称为 J ( y)的变分，记为δJ ( y)，即

（7.1.7）

下面我们证明，泛函 J ( y)取极值的必要条件是

δJ( y) = 0 （7.1.8）或者

（7.1.9）

设 y =y(x) 使泛函 J ( y)取极值，取函数 y(x)变分的特殊形式为

δy(x) = εϕ(x)

式中， ε是任意小的实数；ϕ(x)是充分光滑的任意函数，并且满足条件

ϕ(a) = 0, ϕ(b) = 0

这样，函数

y(x) +εϕ(x) 满足边界条件式（7.1.5）。因此，泛函 J[ y(x) +εϕ(x)]

当 ε= 0时取最小值 J[ y(x)] ，从而有

 

由于

则有

（7.1.10）

以 ε乘式（7.1.10），且 δy(x) =εϕ(x)

则有

应用分部积分，我们作进一步的分析，有

由ϕ(x)的任意性，可得

（7.1.11）

式（7.1.11）称为欧拉－拉格朗日方程，简记为 E-L方程，

必要条件

y =y(x) 使泛函式（7.1.6）取极小值，则 y =y(x) 一定使欧拉－拉格朗日方程式（7.1.11）满足边界条件式（7.1.5）的解。

我们把满足 E-L方程边值问题的解称为驻留函数，对应的积分曲线称为驻留曲线。严格地讲，E-L方程边值问题的解满足变分问题的必要条件，因此它是否是极值函数，还需作进一步的判别。在实际问题中，极值的存在性通常给出问题时已经肯定了，这样，当一个实际现象已知其有唯一的极值存在，而这时也只得到一个驻留函数，则可以判定这个驻留函数就是极值函数。

最终解答

解

且y(0)=0,y(p)=q

这样

（7.1.12）

其E-L方程为

由于

所以有

（7.1.13）

将（7.1.12）代入式（7.1.13）

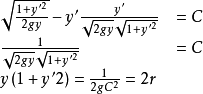
（7.1.14）

引入变量代换x=x(θ)，并设y'=cot(θ/2)

则由式（7.1.14）可得

上式对θ求导，得

所以

 

根据曲线过原点(0,0)及(p,q)可求出x0=0及r，这样，所求曲线为[1]