A Discriminatively Trained, Multiscale, Deformable Part Model

最新推荐文章于 2024-10-08 11:00:19 发布

原创最新推荐文章于 2024-10-08 11:00:19 发布 · 836 阅读

0 ·

CC 4.0 BY-SA版权

计算机视觉专栏收录该内容

219 篇文章

订阅专栏

本文提出了一种基于潜在支持向量机（LSVM）训练的多尺度可变形部分模型，用于目标检测。模型结合了HOG特征、滤波器和可变形部分，通过半凸性训练策略提高性能。在2006和2007年的PASCAL人物检测挑战赛中，系统表现出色，显著提升了平均精度。该方法不仅适用于刚性模板，也适用于高度可变形的目标，且能在有限的训练数据下取得良好效果。

部署运行你感兴趣的模型镜像

参考 A Discriminatively Trained, Multiscale, Deformable Part Model - 云+社区 - 腾讯云

摘要

本文提出了一种可训练的、多尺度、可变形的目标检测零件模型。在2006年PASCAL人员检测挑战赛中，我们的系统在平均精度上比最佳性能提高了两倍。在2007年的挑战赛中，它在20个类别中的10个项目中都取得了优异的成绩。该系统严重依赖于可变形部件。虽然可变形部件模型已经变得相当流行，但它们的价值还没有在PASCAL挑战等困难的基准测试中得到证明。我们的系统还严重依赖于新方法的区别训练。我们将边缘敏感的数据挖掘方法与一种形式主义相结合，我们称之为潜在支持向量机。隐式支持向量机与隐式CRF一样，存在非凸训练问题。然而，隐式SVM是半凸的，一旦为正例指定了潜在信息，训练问题就变成了凸的。我们相信，我们的训练方法最终将使更多的潜在信息的有效利用成为可能，如层次(grammar)模型和涉及潜在三维姿态的模型。

1、简介

我们考虑在静态图像中检测和定位一般类别目标(如人或车)的问题。为解决这一问题，提出了一种新的多尺度可变形零件模型。这些模型使用一个判别过程进行训练，该过程只需要对正样本使用包围框标签。利用这些模型，我们实现了一个高效、准确的检测系统，在大约2秒的时间内处理一幅图像，并实现了明显优于以前系统的识别率。

在2006年PASCAL人物检测挑战赛中，我们的系统比获奖系统的平均精度提高了两倍。在2007年的挑战中，该系统在20个目标类别中有10个类别的表现超过了最好的结果。图1显示了使用person模型获得的一个示例检测。

目标可以由可变形配置中的部件建模的概念为表示目标类别提供了一个优雅的框架。虽然这些模型在概念上很吸引人，但是在实践中很难确定它们的价值。在困难的数据集上，可变形模型通常会被“概念上较弱”的模型(如刚性模板或特征包)超越。我们的主要目标之一是解决这一性能差距。

我们的模型包括覆盖整个目标的粗全局模板和更高分辨率的部分模板。模板表示梯度特征的直方图，我们有区别地训练模型。然而，我们的系统是半监督的，使用最大边缘框架训练，不依赖于特征检测。我们还描述了一种从弱标记数据中学习零件的简单而有效的策略，我们可以在一个CPU上用3小时学习一个模型。

我们工作的另一项贡献是一种区别对待训练的新方法。总结了支持向量机处理零件位置等潜在变量的方法，提出了一种在训练过程中挖掘“难负”实例的新方法。我们认为，处理部分标记的数据是计算机视觉、机器学习中的一个重要问题。例如，PASCAL数据集仅为目标的每个正样本指定一个边界框。我们把每个物体部件的位置看作一个潜在变量。我们还将目标的确切位置作为一个潜在变量，只需要我们的分类器选择一个与标记的边界框有较大重叠的窗口。

隐式支持向量机与隐式CRF一样，存在非凸训练问题。然而，与隐式CRF不同的是，隐式SVM是半凸的，一旦为正训练实例指定了隐式信息，训练问题就变成了凸的。这就引出了潜在支持向量机的一般坐标下降算法。

系统概览：我们的系统使用扫描窗口方法。目标的模型由全局“根”过滤器和几个部分模型组成。每个部件模型指定一个空间模型和一个部件过滤器。空间模型定义了一组相对于检测窗口的部件的允许位置，以及每个位置的变形成本。

检测窗口的分值是根过滤器在窗口上的分值加上部分的和，该部分的最大位置超过该部分，部分过滤器在最终子窗口上的分值减去变形成本。这类似于经典的基于部件的模型。根过滤器和部分过滤器都是通过计算一组权重与窗口内梯度直方图(HOG)特征之间的点积来得分的。根过滤器相当于Dalal-Triggs模型。该部分滤波器的特征值是根滤波器空间分辨率的两倍。我们的模型是在一个固定的尺度下定义的，我们通过搜索一个图像金字塔来检测目标。

在训练中，我们会得到一组图像，这些图像在目标的每个实例周围用包围框标注。将检测问题简化为二分类问题。每个例子x是得分的一个函数形式 $\large f_{\beta}(x)=max_z \beta \Phi(x,z)$ 。β是一个向量的模型参数和z是潜在的值(例如配售部分)。为了学习一个模型，我们定义了一个广义的支持向量机，我们称之为潜在变量支持向量机(LSVM)。LSVMs的一个重要性质是，如果我们对正例的潜值进行修正，训练问题就会变得凸。这可以用在坐标下降算法中。在时间中我们反复迭代训练三元组 $\large (\left \langle x_1,z_1,y_1 \right \rangle,...,\left \langle x_n,z_n,y_n \right \rangle)$ ，其中，在前一次迭代学习的模型中，zi被选为xi的最佳得分潜标。初始根过滤器是从PASCAL数据集中的包围框生成的。这些部分是从这个根过滤器初始化的。

在实践中，我们迭代应用经典的支持向量机训练到三元组，其中被选为在之前迭代学到的模型下的最佳评分潜标签。从PASCAL数据集中的包围框中生成一个初始根筛选器。部件从这个根筛选器初始化。

2、模型

我们模型的基本构建块是来自方向梯度(HOG)特征的直方图。我们在两个不同的尺度上表示HOG特性。粗特征由覆盖整个检测窗口的刚性模板捕获。可以根据检测窗口移动的部件模板捕获更精细的尺度特性。零件位置的空间模型相当于星图或1-fan，其中粗模板作为参考位置。

2.1、HOG表示

我们遵循HOG人脸检测器中的构造来定义特定分辨率下图像的密集表示。首先将图像划分为8x8个不重叠的像素区域，即单元格。对于每个单元格，我们在该单元格中累积像素上梯度方向的一维直方图。这些柱状图捕捉局部形状特性，但对小变形也有一定的不变性。

每个像素处的梯度被离散成9个方向箱中的一个，每个像素为其梯度的方向“投票”，其强度取决于梯度的大小。对于彩色图像，我们计算每个颜色通道的梯度，并在每个像素处选取梯度幅度最大的通道。最后，将每个细胞的直方图相对于其周围区域的梯度能量进行归一化。我们观察包含特定细胞的4个2×2的细胞块，并将给定细胞相对于每个细胞块中的总能量的直方图标准化。这样就得到一个长度为9×4的向量，表示单元格内的局部梯度信息。

我们定义了一个HOG特征金字塔通过计算每一层的功能标准图像金字塔(参见图2)。特性这金字塔的顶部捕捉粗输入图像的梯度直方图在相当大的区域在金字塔的底部特征捕获细梯度直方图在很小的区域。

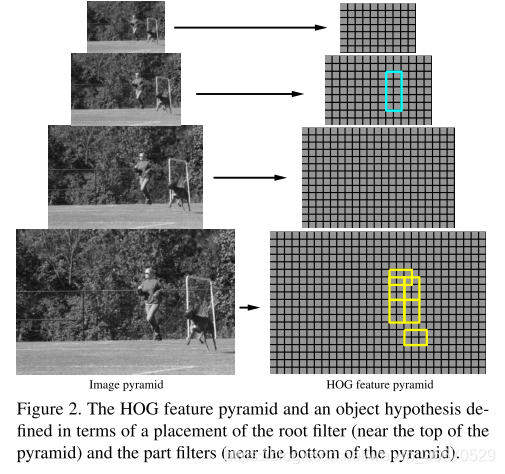
2.2、滤波器

滤波器是指定HOG金字塔子窗口权重的矩形模板。一个w×h滤波器F是一个权值为w×h×9×4的向量。滤波器的得分是通过对权重向量和HOG金字塔的w×h子窗口的特征点积来定义的。HOG人脸检测器中的系统使用一个过滤器来定义目标模型。

该系统通过对HOG金字塔的每个w×h子窗口进行打分并对分数进行阈值化，从而检测来自特定类的目标。

设H为一个HOG金字塔，为金字塔第l层的一个细胞。让表示向量通过连接HOG特性H和w×H好子窗口的左上角的分数p。在这个检测窗口。下面我们用来表示当维度从上下文。

2.3、可变形部分

在这里，我们考虑由覆盖整个目标的粗根过滤器和覆盖目标较小部分的高分辨率部分过滤器定义的模型。图2说明了这样一个模型在HOG金字塔中的位置。根过滤器位置定义检测窗口(过滤器覆盖的单元格内的像素)。部分过滤器被放置在金字塔的几层下面，所以在这一层的HOG细胞只有根过滤器层单元大小的一半。

我们发现，使用更高分辨率的特征来定义部件过滤器对于获得更高的识别性能至关重要。使用这种方法，与根过滤器中表示的边缘相比，部件过滤器表示更细的分辨率边缘，这些边缘的定位精度更高。例如，考虑为人脸构建一个模型。根滤波器可以捕捉人脸边界等粗分辨率边缘，而局部滤波器可以捕捉眼睛、鼻子和嘴巴等细节。

具有n个部件的目标模型由根过滤器和一组部件模型，其中。是第 $i$ 部分过滤， $v_i$ 是一个二维向量指定一盒中心部分的可能位置我相对于根的位置，如果让这个盒子的大小，而 $a_i$ 和 $b_i$ 是二次函数的二维向量指定系数测量得分为每个第 $i$ 部分的可能位置。图1演示了一个person模型。

模型在HOG金字塔中的位置由，其中为 $i = 0$ 时根滤波器的位置，当 $i$ d大于零时，第 $i$ 部分的位置。我们假设每个部分的级别都是这样的：在该级别上的HOG单元格只有根级别上的HOG单元格的一半大小。一个位置的得分由每个过滤器的得分(数据项)加上每个部分相对于根位置的位置得分(空间项)给出，

$\large \sum_{i=0}^n\phi (H,p_i)+\sum_{i=1}^n a_i\cdot(\tilde{x_i},\tilde{y_i})+b_i\cdot(\tilde{x_i}^2,\tilde{y_i}^2)$

其中 $\large (\tilde{x_i},\tilde{y_i})=((x_i,y_i)-2(x,y)+v_i)/s_i$ 给出第 $i$ 部分相对于根位置的位置。 $\large \tilde{x}_i$ 和 $\large \tilde{y}_i$ 应该在-1到1之间。

在HOG金字塔模型中，有大量的(指数)位置。我们使用动态规划和距离变换技术计算模型各部分的最佳位置作为根位置的函数。这需要 $O(nk)$ 时间，其中n为模型中的部件数， $k$ 为HOG金字塔中的细胞数。为了检测图像中的目标，我们根据部件的最佳位置和阈值对根位置进行评分。z得分的位置可以表示的点积，之间的矢量模型参数和

$\large \beta=(F_0,...,F_n,a_1,b_1,...,a_n,b_n)\\ \psi (H,z)=(\phi (H,p_0),\phi (H,p_1),...,\phi (H,p_n),\tilde{x}_1,\tilde{y}_1,\tilde{x}_1^2,\tilde{x}_1^2,...,\tilde{x}_n,\tilde{y}_n,\tilde{x}_n^2,\tilde{x}_n^2)$

我们使用这种表示学习模型参数，因为它使我们的变形模型和线性分类器之间的联系。

这里定义的空间模型的一个有趣的方面是，我们允许系数为负。这比以前工作中使用的二次“spring”成本更普遍。

3、学习

PASCAL训练数据由大量图像组成，每个目标实例周围都有包围框。将利用该数据学习可变形零件模型的问题简化为二分类问题。设 $\large D=(\left \langle x_1,y_1 \right \rangle,...,\left \langle x_n,y_n \right \rangle)$ 是一组标记示例，其中和 $x_i$ 指定了一个HOG金字塔， $H(x_i)$ ，以及根和部分滤波器器的有效位置范围Z(xi)。根和有效位置的部分我们从训练集中的每个边界框构造一个正样本。对于这些例子，我们定义 $Z(x_i)$ ，因此必须放置根过滤器以使边界框重叠至少50%。负样本来自不包含目标的图像。在这样的图像中，每次放置根过滤器都会产生一个负面的训练示例。

注意，对于正样本，我们将部件位置和根过滤器的确切位置都视为潜在变量。我们发现，在训练过程中允许根位置的不确定性可以显著提高系统的性能(参见第4节)。

3.1、Latent SVM

一个潜在的SVM定义如下。我们假设每个例子 $x$ 都是由这个形式的函数得分的，

$\large f_\beta(x)=max_{z\in Z(x)}\beta\Phi (x,z)$ (2)

β是一个向量的模型参数和z是一组潜在的价值。我们为我们的可变形模型定义，这样的分数将根据z模型。在类比经典支持向量机我们想从标记示例 $\large D=(\left \langle x_1,y_1 \right \rangle,...,\left \langle x_n,y_n \right \rangle)$ ，通过优化以下目标函数，

$\large \beta^*(D)=\mathop{\arg\min}_{\beta}\lambda \ \ \|\beta\|^2+\sum^n_{i=1}max(0,1-y_if_{\beta}(x_i)).$

通过限制潜在的域 $\large Z(x_i)$ 单一选择， $\large f_{\beta}$ 在 $\large \beta$ 中是线性的，并且我们得到线性SVM作为latent SVM的特殊情况。潜在支持向量机是基于能量的一般模型的实例。

3.2、半凸性

注意上式定义的 $\large f_\beta(x)$ 的定义是函数的最大值，每一个在 $\large \beta$ 中都是线性的。因此在 $\large \beta$ 中 $\large f_\beta(x)$ 是凸的。这意味着当 $\large y_i=-1$ hinge loss $\large max(0,1-y_if_\beta(x_i))$ 在 $\large \beta$ 是凸的。我们称损失函数的这个性质为半凸性。

考虑一个LSVM，其中正例的潜在域Z(xi)被限制为一个选择。由于每个正的例子，损失现在是凸的。结合semi-convexity属性,(3)成为β凸。

如果正例的标签不是固定的，我们可以使用坐标下降算法计算(3)的局部最优值:

固定 $\large \beta$ ，优化正例的潜在值
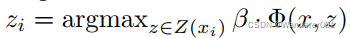
对正样本使 $\large \{z_i\}$ 固定，优化β通过求解凸问题上面定义

它可以表明，这两个步骤总是改善或维持的价值(3)的目标函数。如果两个步骤保持我们有强烈的局部最优值(3)，在某种意义上，第一步搜索一个指数大空间的潜在标签正面例子，而第二步同时搜索权重向量和一个指数大空间)潜在的负面标签的例子。

3.3、难负数据挖掘

在目标检测中，绝大多数训练示例是负的。这使得一次性考虑所有负面的例子是不可行的。相反，训练数据通常由积极实例和“硬否定”实例组成，其中硬否定是从大量可能的消极实例中挖掘出来的数据。

在此，我们描述了一种通用的方法，用于支持向量机和潜在支持向量机的数据挖掘实例。该方法仅使用硬实例迭代求解子问题。该方法的创新在理论上保证了它能够精确地解决使用完整训练集定义的训练问题。我们的结果需要使用硬例子的边界敏感定义。

这里描述的结果既适用于经典的支持向量机，也适用于潜伏支持向量机的坐标下降算法的步骤2所定义的问题。由于篇幅有限，我们省略了这些定理的证明。这些结果与工作集方法[17]有关。

我们将D相对于β的硬实例定义为：

也就是说，是被错误分类或接近β定义的分类器边缘的训练示例。我们可以证明，只依赖于硬实例。

定理1

假设 $C$ 是 $D$ 中示例的子集，如果

这意味着在原则上，我们可以使用一小组示例来训练一个模型。然而，这个集合是根据最优模型定义的。

给定一个固定的 $\beta$ ，我们可以使用来近似。这表明了一种迭代算法，我们可以从上次迭代的模型定义的硬实例中反复计算一个模型。下面的不动点定理进一步证明了这一点。

定理2

如果

让 $C$ 作为示例的初始“缓存”。在实践中，我们可以把积极的例子和随机的消极的例子结合起来。考虑以下迭代算法：

1. 让

2. 通过让收缩 $C$ 。

3.通过添加从到内存限制L的示例来增长 $L$ 。

3.4、实现细节

这里讨论的许多想法只是在我们当前的系统中大致实现。在实践中，在训练一个潜在SVM时，我们迭代地将经典SVM训练应用到 $\large \left \langle x_1,y_1,z_1 \right \rangle ,..., \left \langle x_n,y_n,z_n \right \rangle$ 三组中，在前一次迭代训练的模型中，选取zi作为xi的最佳得分潜在标签。这些三元组中的每一个都指向一个用于训练线性分类器的示例 $\large \left \langle \Phi (x_i,z_i) ,y_i\right \rangle$ 。这允许我们使用高度优化的SVM包。在单个CPU上，PASCAL数据集中每个目标类的整个训练过程需要3到4个小时，包括部件的初始化。

根滤波器初始化

根过滤器初始化：对于每个类别，我们通过查看训练数据中包围框的统计信息，自动选择根过滤器的维度。我们使用一个没有潜在变量的SVM训练一个初始根滤波器。正样本由未包含的训练示例构造(如PASCAL数据中所示)。这些例子是各向异性比例的大小和宽高比的过滤器。我们使用随机子窗口从负图像生成负样本。

根滤波器更新

给定如上所训练的初始根过滤器，对于训练集中的每个边界框，我们找到与边界框明显重叠的过滤器的最佳得分位置。我们使用原始的，未缩放的图像。我们用新的正集和原来的随机负集重新训练，迭代两次。

部件初始化

我们使用一个简单的启发式方法从上面训练的根过滤器初始化六个部分。首先，我们选择一个面积a，使6a等于根滤波器面积的80%。我们贪婪地从正能量最大的根滤波器中选择面积a的矩形区域。我们把这个区域的权重归零，然后重复，直到选择了六个部分。部件筛选器从为部件选择的子窗口中的根筛选器值初始化，但填充后处理部件的更高空间分辨率。初始变形成本度量和时位移的平方模量。

模型更新

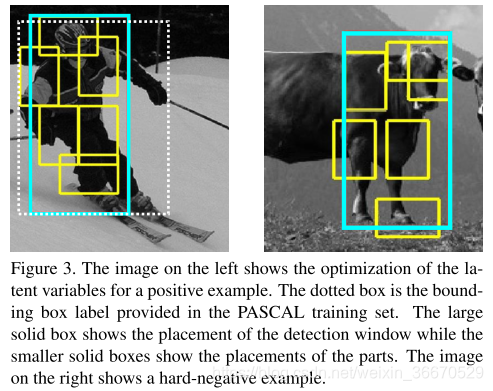
为了更新模型，我们构造了新的训练数据三元组。对于训练数据中的每个正边界盒，我们将现有的检测器应用于所有位置和尺度，且与给定边界盒重叠至少50%。其中，我们选择得分最高的位置作为与此训练边界框对应的正例(图3)。我们向缓存添加负样本，直到遇到文件大小限制。利用支持向量机对正、负样本分别进行光照训练，每个样本用零件位置标记。我们使用上面描述的缓存方案对模型进行了10次更新。在每个迭代中，我们从以前的缓存中保留难例，并在内存限制内添加尽可能多的难例。对最终的迭代,我们能够包括所有困难的情况下在缓存中。

4、结果

我们使用PASCAL VOC 2006和2007 comp3 challenge数据集和协议对系统进行了评估。强调这两个挑战都被广泛认为是目标检测的困难测试平台。每个数据集包含数千幅真实世界场景的图像。数据集为几个目标类指定了ground-truth边界框，当与ground-truth边界框重叠超过50%时，检测就被认为是正确的。其中一种方法是通过测试集上的精确召回曲线的平均精度(AP)来给系统打分。

最近在行人检测方面的工作倾向于报告每个窗口的检出率与误报率的比较，测量时使用的是经过剪裁的正样本和没有感兴趣的目标阴性图像。这些分数与扫描窗口搜索的分辨率有关，忽略了非最大抑制的效果，使得比较不同系统变得困难。我们相信PASCAL评分方法提供了一个更可靠的性能度量。

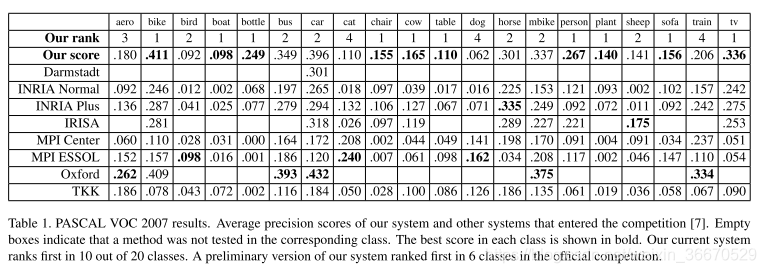
2007年的挑战有20个目标类别。我们在正式比赛中进入了系统的初版，并在6个类别中获得了最好的成绩。我们目前的系统在10个类别中得分最高，在6个类别中得分第二。表1总结了结果。

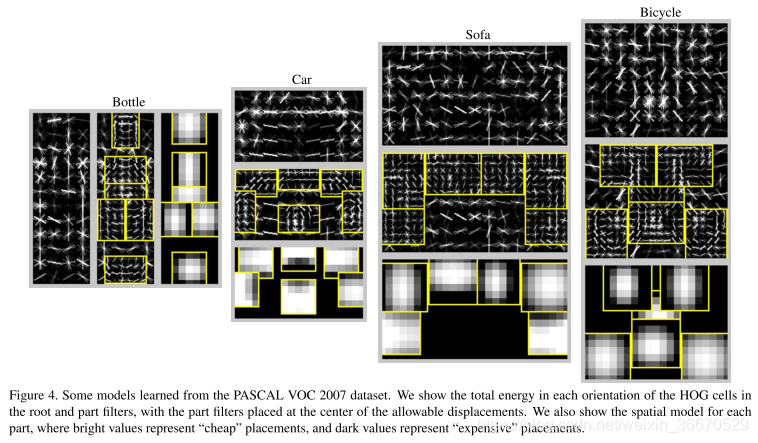
我们的系统适用于刚性物体，如汽车和沙发，以及高度可变形的物体，如人和马。我们还注意到，当提供大量或少量训练数据时，我们的系统是成功的。在人员类别中大约有4700个正训练样本，但，在沙发类别中只有250个。图4显示了我们学习的一些模型。图5显示了一些示例检测。

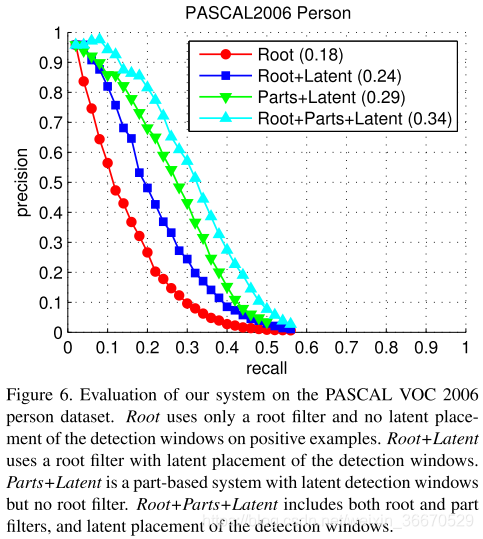
我们在较长时间建立的2006个人数据集上评估了系统的不同组件。在PASCAL竞赛中，使用HOG特征的刚性模板模型获得的AP最高分为0.16分。.19之前的最佳结果添加了基于分段的验证步骤。图6总结了我们训练的几个模型的性能。我们的根模型等价于的模型，它的得分略高，为.18。当使用LSVM对模型进行训练时，性能跃升到0.24,LSVM为每个正例选择一个潜在位置和比例。这表明LSVMs甚至对于刚性模板也是有用的，因为它们允许在训练示例中自调整检测窗口。添加可变形部件可将性能提高到0.34 ap—比之前的最佳评分高出两倍。最后，我们训练了一个有部分但没有根滤波器的模型，得到.29的AP。这说明了使用多尺度表示的优点。

我们还研究了空间模型和允许变形对2006人数据集的影响。回想一下 $s_i$ 是一个部分的允许位移，在HOG单元中测量。我们通过将si设置为0来训练具有高分辨率部件的刚性模型。该模型的性能比纯根系统高出0.27到0.24。如果我们在不考虑变形代价的情况下增加允许位移量，我们就开始接近特征包。性能在si = 1处达到峰值，说明约束零件位移是有用的。该优化策略允许较大的位移，同时使用显式变形成本。下表显示了AP作为前三列自由允许变形的函数。最后一列给出了使用二次变形代价和2个HOG单元的允许位移时的性能。