快速注意,这几乎肯定会混淆Big O符号(这是一个上限)与Theta符号(这是一个双边界限)。根据我的经验,这实际上是非学术环境中的典型讨论。对所引起的任何混乱道歉。
使用此图可以显示Big O复杂度:
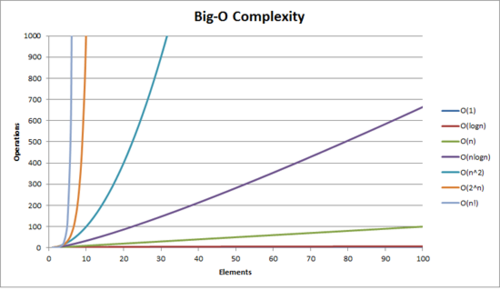
我可以为Big-O表示法给出的最简单的定义是:
Big-O表示法是算法复杂性的相对表示。
在这句话中有一些重要且刻意选择的词:亲戚:你只能比较苹果和苹果。您无法将算法与算术乘法进行比较,而是对整数列表进行排序。但是比较两个算法进行算术运算(一次乘法,一次加法)会告诉你一些有意义的东西;
表示: Big-O(最简单的形式)减少了算法与单个变量之间的比较。该变量基于观察或假设来选择。例如,通常基于比较操作来比较排序算法(比较两个节点以确定它们的相对排序)。这假设比较昂贵。但是,如果比较便宜但交换费用昂贵呢?它改变了比较; 和
复杂性:如果需要一秒钟才能对10,000个元素进行排序,那么我需要多长时间才能排序一百万个元素?在这种情况下,复杂性是对其他事物的相对衡量。
当你读完其余部分后,回过头来重读上面的内容。
我能想到的Big-O最好的例子就是做算术。取两个数字(123456和789012)。我们在学校学到的基本算术运算是:加成;
减法;
乘法; 和
师。
这些都是操作或问题。解决这些问题的方法称为算法。
增加是最简单的。您将数字向上排列(向右)并在列中添加数字,在结果中写入该添加的最后一个数字。该数字的“十”部分将转移到下一列。
让我们假设添加这些数字是该算法中最昂贵的操作。按理说,要将这两个数字加在一起,我们必须将6位数加在一起(并且可能带有7位数)。如果我们将两个100位数字加在一起,我们必须做100次加法。如果我们添加两个 10,000位数字,我们必须进行10,000次添加。
看模式?的复杂性(即操作的次数)正比于数字数量Ñ在较大的数量。我们称之为O(n)或线性复杂度。
减法是类似的(除了你可能需要借用而不是随身携带)。
乘法是不同的。你将数字排成一行,取下面数字中的第一个数字,然后依次将它与顶部数字中的每个数字相乘,依此类推。因此,要将两个6位数相乘,我们必须进行36次乘法运算。我们可能需要多做10或11列添加才能获得最终结果。
如果我们有两个100位数字,我们需要进行10,000次乘法和200次加法。对于两百万个数字,我们需要进行一万亿(10 12)次乘法和两百万次加法。
当算法按n 平方缩放时,这是O(n 2)或二次复杂度。这是介绍另一个重要概念的好时机:
我们只关心复杂性中最重要的部分。
精明的人可能已经意识到我们可以将操作次数表示为:n 2 + 2n。但正如你从我们的例子中看到的那样,每个数字有两个数字,第二项(2n)变得微不足道(占该阶段总运算的0.0002%)。
人们可以注意到我们已经假设了最糟糕的情况。如果其中一个是4位数而另一个是6位数,则乘以6位数字,那么我们只有24次乘法。我们仍然计算'n'的最坏情况,即当两者都是6位数时。因此,Big-O表示法是关于算法的最坏情况
电话簿
我能想到的下一个最好的例子是电话簿,通常称为白页或类似的,但它会因国家而异。但我说的是那个按姓氏列出人名,然后是姓名首字母或名字,可能是地址,然后是电话号码的人。
现在,如果您指示计算机在包含1,000,000个名字的电话簿中查找“John Smith”的电话号码,您会怎么做?忽略一个事实,你可以猜到S的开始有多远(让我们假设你不能),你会做什么?
一个典型的实现可能是开到中间,拿50万个,并把它比作“史密斯”。如果恰好是“史密斯,约翰”,我们真的很幸运。更有可能的是,“约翰史密斯”将在该名称之前或之后。如果是在我们之后,我们将电话簿的后半部分分成两半并重复。如果是在那之前,我们将电话簿的前半部分分成两半并重复。等等。
这称为二进制搜索,无论您是否意识到,它每天都会在编程中使用。
因此,如果您想在一百万个名字的电话簿中找到一个名字,您最多可以通过这样做20次来找到任何名称。在比较搜索算法时,我们认为这种比较是我们的'n'。对于3个名字的电话簿,它需要进行2次比较(最多)。
对于7最多需要3个。
15岁需要4个。
...
1,000,000需要20。
那是惊人的好不是吗?
在Big-O术语中,这是O(log n)或对数复杂度。现在,所讨论的对数可以是ln(基数e),log 10,log 2或其他一些基数。无论如何它仍然是O(log n)就像O(2n 2)和O(100n 2)仍然都是O(n 2)。
在这一点上值得解释的是Big O可用于通过算法确定三种情况:最佳案例:在电话簿搜索中,最好的情况是我们在一次比较中找到了名称。这是O(1)或不变的复杂性 ;
预期案例:如上所述,这是O(log n); 和
最坏情况:这也是O(log n)。
通常我们不关心最好的情况。我们对预期和最坏的情况感兴趣。有时这些中的一个或另一个将更重要。
回到电话簿。
如果您有电话号码并想要找到名字怎么办?警方有一本反向电话簿,但这些查询被公众拒绝。或者是他们?从技术上讲,您可以在普通电话簿中反向查找数字。怎么样?
您从名字开始并比较数字。如果它是一场比赛,那么很棒,如果没有,你继续前进。你必须这样做,因为电话簿是无序的(无论如何通过电话号码)。
所以要给出一个给出电话号码的名字(反向查询):最佳案例: O(1);
预期案例: O(n)(500,000); 和
最坏情况: O(n)(1,000,000)。
旅行推销员
这是计算机科学中一个非常着名的问题,值得一提。在这个问题上你有N个城镇。这些城镇中的每一个都通过一定距离的道路与一个或多个其他城镇相连。旅行推销员的问题是找到访问每个城镇的最短旅行。
听起来很简单?再想想。
如果您有3个城镇A,B和C,所有城市之间都有道路,那么您可以去:A→B→C
A→C→B
B→C→A
B→A→C
C→A→B
C→B→A
实际上还不到那个,因为其中一些是等价的(例如,A→B→C和C→B→A是等价的,因为它们使用相同的道路,正好相反)。
实际上有3种可能性。把它带到4个城镇,你有(iirc)12种可能性。
5岁就是60岁。
6变为360。
这是称为阶乘的数学运算的函数。基本上:5!= 5×4×3×2×1 = 120
6!= 6×5×4×3×2×1 = 720
7!= 7×6×5×4×3×2×1 = 5040
...
25!= 25×24×...×2×1 = 15,511,210,043,330,985,984,000,000
...
50!= 50×49×...×2×1 = 3.04140932×10 64
因此,旅行商问题的大O是O(n!)或阶乘或组合复杂性。
当你到达200个城镇时,宇宙中没有足够的时间来解决传统计算机的问题。
需要考虑的事情。
多项式时间
我想要快速提及的另一点是,任何具有O(n a)复杂度的算法都被认为具有多项式复杂性或者在多项式时间内是可解的。
O(n),O(n 2)等都是多项式时间。有些问题在多项式时间内无法解决。因此,世界上使用了某些东西。公钥加密是一个很好的例子。在计算上很难找到两个非常大的素数因子。如果不是,我们就无法使用我们使用的公钥系统。
无论如何,这就是我对Big O(修订版)的解释(希望是简单的英语)。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








