5阶无向完全图_学习数据结构--第五章：图（图的基本知识）

第五章：图(图的基本知识)

1.图的基本概念

图 图G由顶点集V和边集E组成,记为G=(V,E),其中V(G)表示图G中顶点的有限非空集；E(G)表示图G中顶点之间的关系(边)集合

|V| 表示图G中顶点的个数，也称图G的阶；|E|表示图G中边的条数(| |代表绝对值)

注意：线性表、树都可以为空，但是图不能为空

2.无向图&有向图

上面我们讲解的图，就是一个无向图，它的边集使用的圆括号组成的一个集合，为什么使用的圆括号？其实这样的圆括号表示的就是无向边。

无向边：表示这个边是没有方向的，它并不区分起始和终止，所以我们可以使用这样的无序对(V,W) = (W,V)来表示，也可以说V,W互为邻接点

无向图：在该图中所有的边都是无向边

有向图：在该图中所有的边都是有向边

有向边：该边是有方向的，它区分起始位置和终止位置，V------->W，我们也称这样有向边为弧，称起始位置为弧头，终止位置为弧尾。我们使用有序对来表示，这时候就要区分和了，我们也称V邻接到W或W邻接自V

3.简单图&多重图

简单图：无重复边，或不存在节点到自身的边。

多重图：存在重复的边，或存在结点到自身的边。

注意：下面的图虽然出现了A指向B，B指向A，但这不是重复的边，不是多重图，我们在上面讲有向图的时候讲到和是代表不同的边的，所以它不是多重图。

4.完全图

完全图：分为无向完全图和有向完全图

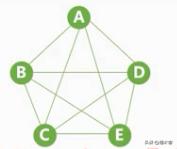
无向完全图：

• 任意两个顶点之间都存在边
• n个顶点有 n(n-1)/2个边

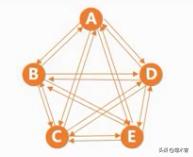
有向完全图：

• 任意两个顶点之间都存方向相反的在弧
• n个顶点有 n(n-1)个边

5.子图

设有两个图 G=(V,E)和 G'=(V',E')，若 V‘ 是 V的子集，且 E’是 E的子集，则称 G‘ 为 G的子图，且若 V(G) = V(G')则称G'为G的生成子图

6.无向图&有向图

无向图：只有连通：若从顶点V到顶点W有路径存在，则称V和W是连通

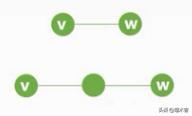
连通图：任意两个结点都是连通的

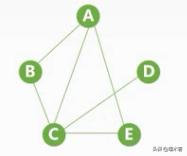
有向图：只有强连图：若从顶点V到顶点W 和 从顶点W到顶点V都有路径存在，则称V和W是强连通

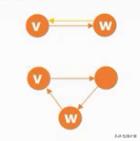
强连通图：任意两个结点都是强连通的

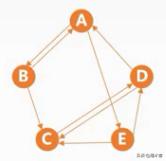
n个顶点的连通图(强连通图)最少有多少条边？

连通图：n-1 【某一个顶点与剩余的每一个顶点(n-1)有一条边】

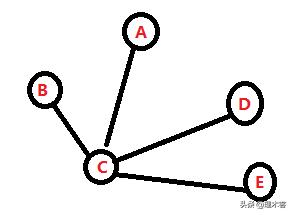
强连通图：n

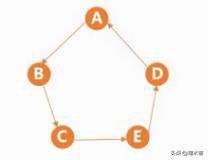
无向图的连通分量：极大连通子图

有向图的强连通分量：极大强连通子图

对于G的一个(强)连通子图G'·,如果不存在G的另一个(强)连通子图G",使得G属于G",则称G'为G的(强)连通分量(就是该连通分量一定是最大的那个，不存在另外的连通子图或者强连通子图能够把它包含起来，即保证他是连通的或者强连通的情况下能够包含更多的顶点和边)

我们看几个例子：找出无向图立的连通分量

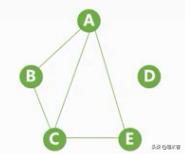
首先画出它的几个连通子图，找出连通分量(极大连通子图)

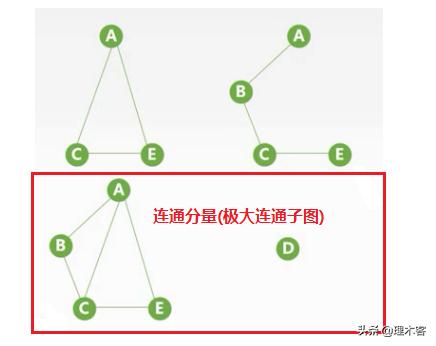
我们可以看出下面两个是连通分量(极大连通子图)，因为其他的连通子图，都不能包含他们。

找出有向图立的连通分量

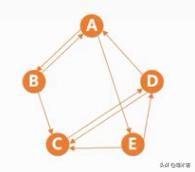
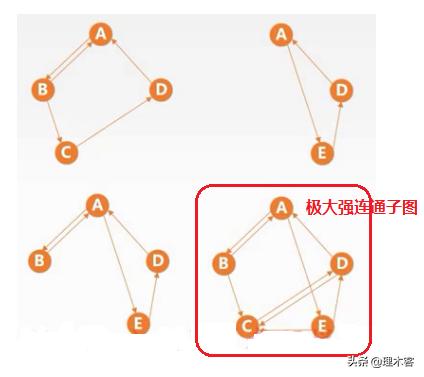
上面的无向图有两个连通分量，而有向图只有一个连通分量。其实我们可以得出一个结论：如果一个图他是连通图或者强连通图，那个它的连通分量或强连通分量就是他自己，而如果一个图不是连通图或者强连通图，那么它的连通分量或者强连通分量则会有许多个。

7.生成树、生成森林

极小连通子图：连通子图且包含的边最少

在满足连通的情况下达到边最少

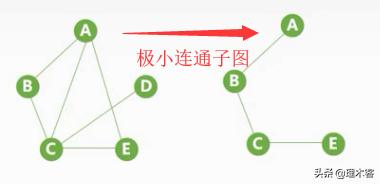
生成树：连通图包含全部顶点的一个极小连通子图

首先原图一定是一个连通通，然后包含全部顶点的一个极小连通子图

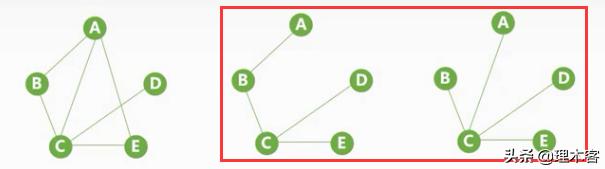
n个顶点的图的生成树有n-1条

(连通图只能生成生成树，非连通图只能生成生成森林)

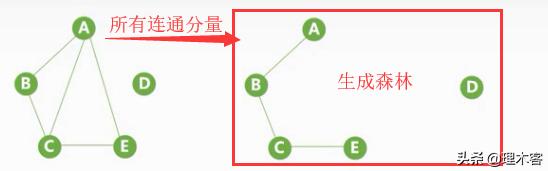
生成森林：非连通图所有连通分量的生成树组成森林

8.顶点的度

顶点的度：以该顶点为一个断点的边的数目

无向图：顶点V的度以V为断点边的个数记为TD(V)

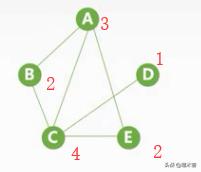
n个顶点，e条边的无向图中度的总数为：2e

有向图：

• 出度：以V为起点的有向边的条数，记作 OD(V)
• 入度：以V为终点的有向边的条数，记作 ID(V)

n个顶点，e条边的有向图中出度，入度总数分别为：e:

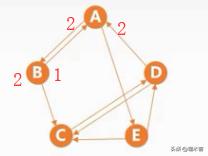
9.网

为边赋予权重(在实际情况中可能是花费时间等)

10.稠密图&稀疏图

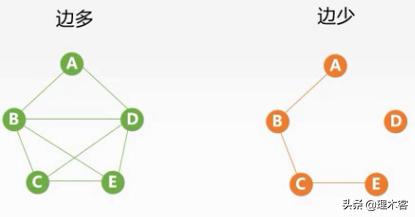
稀疏稠密的界定：|E|

当变数小于结点数乘以log结点数的时候称为稀疏图

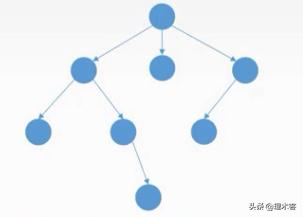
11.有向树

有向树：一个顶点的入度为0、其余顶点的入度均为1的有向图

12.路径

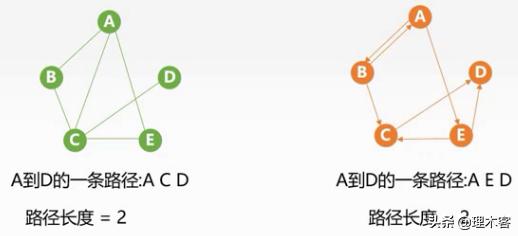
路径：图中顶点V到顶点W的顶点序列，序列中顶点不重复的路径称为简单路径

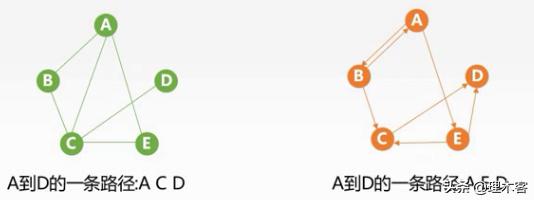
路径长度：路径上边的数目，若该路径最短则称其为距离

回路：第一个顶点和最后一个顶点相同的路径(环状结构)

关于数据结构的知识公众号 理木客同步更新中，下次将会讲解：图的存储及基本操作，期待大家的关注