图论计算机,图论

物间宁人

于 2021-07-25 15:16:27 发布

阅读量1.2k

点赞数

文章标签：图论计算机

图论是数学和计算机科学中的一个重要分支，它通过图来建模对象之间的关系。无向图和有向图是两种基本类型，广泛应用于网络理论、路径规划、数据组织等领域。1736年的哥尼斯堡七桥问题是图论的早期起源，而四色猜想的证明则是图论历史上的里程碑。随着计算机科学的发展，图论在解决实际问题中扮演着越来越关键的角色，未来将深入研究超大图、跨学科交叉及复杂计算问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

图论是以“图”为研究对象的一个数学分支，是组合数学和离散数学的重要组成部分。图是用来对对象之间的成对关系建模的数学结构，由“顶点”(又称“节点”或“点”)以及连接这些顶点的“边”(又称“弧”或“线”)组成。值得注意的是，图的顶点集合不能为空，但边的集合可以为空。图可能是无向的，这意味着图中的边在连接顶点时无需区分方向。否则，称图是有向的。下面左图是一个典型的无向图结构，右图则属于有向图。

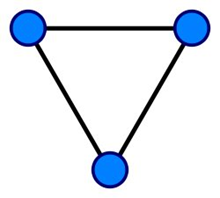
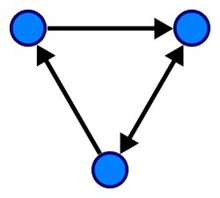
图可用于在物理、生物、社会和信息系统中建模许多类型的关系和过程。许多实际问题可以用图来表示。因此，图论成为运筹学、控制论、信息论、网络理论、博弈论、物理学、化学、生物学、社会科学、语言学、计算机科学等众多学科强有力的数学工具。在强调其应用于现实世界的系统时，网络有时被定义为一个图，其中属性(例如名称)之间的关系以节点和/或边的形式关联起来。

在计算机科学中,图用来表示通信、数据组织、计算设备、计算流等网络，在社交媒体、计算机芯片设计、自然语言处理、路径规划等很多方面有广泛应用。例如,网页之间的链接结构可以表示为一个有向图，其中顶点代表网页而有向的边表示从一个页面链接指向另一个。

发展历史

描述(300字)

1736年著名数学家Euler关于