如何使用计算机建模,第二讲：数学建模的基本方法和步骤

第二讲数学建模的基本方法和步骤

数学建模面临的实际问题是多种多样的，建模的目的不同、分析的方法不同、采用的数学工具不同，所得模型的类型也不同，我们不能指望归纳出若干条准则，适用于一切实际问题的数学建模方法。下面所谓基本方法不是针对具体问题而是从方法论的意义上讲的。(注：用最初等的方法解决，越受人尊重)

一数学建模的基本方法

一般说来数学建模的方法大体上可分为机理分析和测试分析两种。

??????

???????机理分析：是根据对客观事物特性的认识，找出反映内部机理的数量规律，建立的数学模型常有明确的物理或现实意义。

建模方法

测试分析：将研究对象看作一个“黑箱”(意思是内部机理看不清

楚)，通过对测量数据的统计分析，找出与数据拟合最

好的模型。

面对于一个实际问题用哪一种方法建模，主要取决于人们对研究对象的了解程度和建模目的。如果掌握了一些内部机理的知识，模型也要求具有反映内部特征的物理意义，建模就应以机理分析为主。而如果对象的内部机理规律基本上不清楚，模型也不需要反映内部特征，那么可以用测试分析。对于许多实际问题也常常将两种方法结合起来，用机理分析建立模型结构，用测试分析确定模型的参数。

二数学建模的一般步骤

建模要经过哪些步骤并没有一定的模式，通常与问题性质和建模的目的等有关。下面给出建模的一般步骤，如图1.2所示。

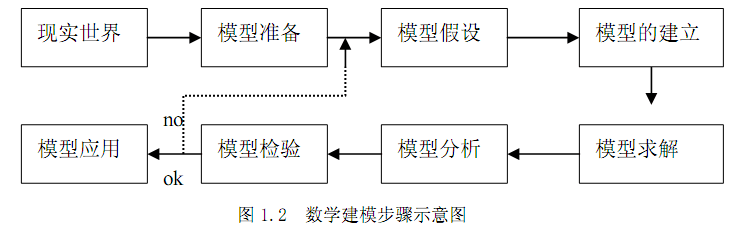
⑴模型准备：了解实际背景，明确建模目的，搜索必要信息，弄清对象的主要特征，形成一个比较清晰的“问题”(即问题的提出)。情况明才能方法对，在这个阶段要深入调查研究，虚心向实际工作者请教，尽量掌握第一手资料。