10. Regular Expression Matching

题目描述(困难难度)

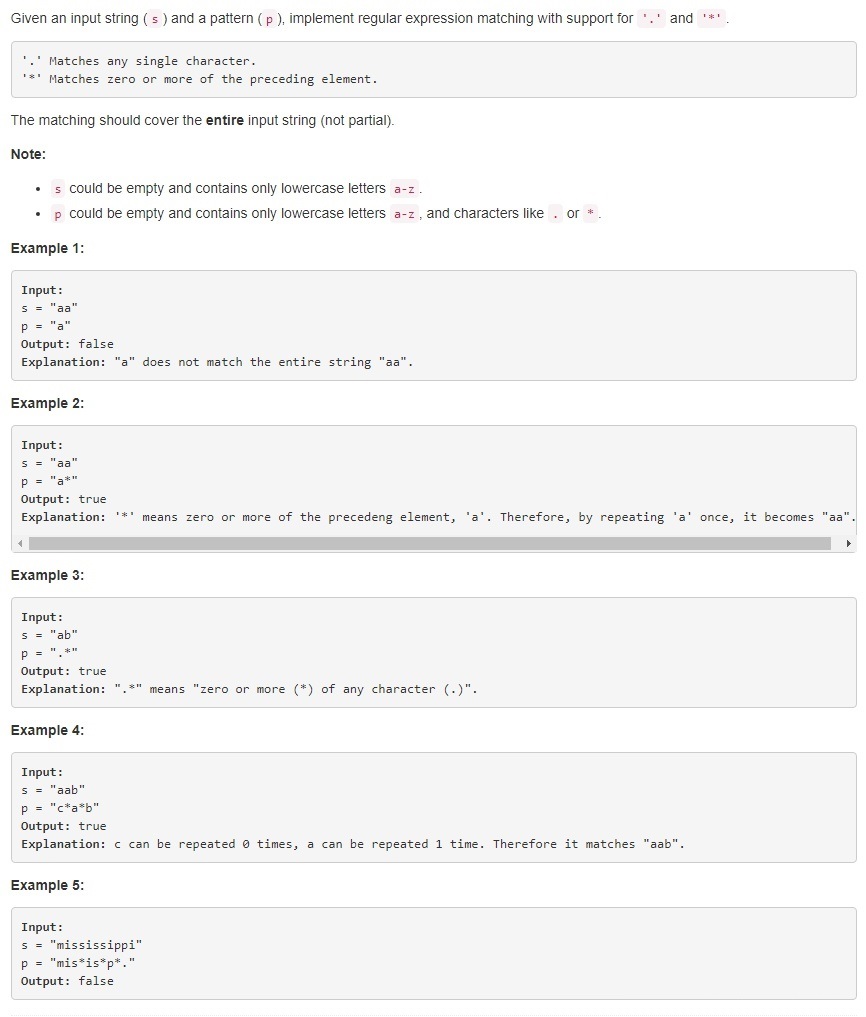
题目大意：判断两个字符是否可以匹配成功，成功则返回True，否则返回False。其中【.】可以匹配任意单个字符，【*】可以匹配前面零个或多个前面那一个元素。

解法一 递归

• 我们假设存在函数 isMatch，它告诉我们 text 和 pattern 是否匹配

boolean isMatch ( String text, String pattern ) ;

• 递归规模减小

text 和 pattern 匹配，等价于 text 和 patten 的第一个字符匹配并且剩下的字符也匹配，而判断剩下的字符是否匹配，我们就可以调用 isMatch 函数。也就是

(pattern.charAt(0) == text.charAt(0) || pattern.charAt(0) == '.')&&isMatch(text.substring(1), pattern.substring(1)); 

随着规模的减小，当pattern为空时，如果text也为空，就返回True，不然的话就返回False。
存在两种情况判断第一个字符是否相同。

if (pattern.isEmpty()) return text.isEmpty(); 

综上，我们的代码是

public boolean isMatch(String text, String pattern) {
        if (pattern.isEmpty()) return text.isEmpty();

        //判断 text 是否为空，防止越界，如果 text 为空， 表达式直接判为 false, text.charAt(0)就不会执行了
        boolean first_match = (!text.isEmpty() &&
                               (pattern.charAt(0) == text.charAt(0) || pattern.charAt(0) == '.'));
        return first_match && isMatch(text.substring(1), pattern.substring(1));
    }

上述代码只考虑了存在【.】这种情况。当我们考虑了 存在【*】的时候，对于递归规模的减小，会增加对于星号的判断。

 public class Regular_Expression_Matching {
        public boolean isMatch(String s, String p) {
        if (p.isEmpty())  return s.isEmpty();
        boolean first_match = (!s.isEmpty() && (s.charAt(0) == p.charAt(0) || p.charAt(0) == '.'));
        if(p.length() >= 2 && p.charAt(1) == '*'){
            return (isMatch(s,p.substring(2)) || (first_match && isMatch(s.substring(1),p)));
        }else{
            return first_match && isMatch(s.substring(1),p.substring(1));
        }
    }
    	public static void main(String args[]) {
    		String text="aab";
    		String pattern="c*a*b";
    		boolean ans=isMatch(text,pattern);
    		System.out.println(ans);
    	}
    }

转换成python版本如下：

class Solution(object):
    def isMatch(self, s, p):
        if (p==""):
            return s==""
        first_match = (s!="" and (s[0] == p[0] or p[0] == '.'))
        if(len(p) >= 2 and p[1] == '*'):
            return (self.isMatch(s,p[2:]) or (first_match and self.isMatch(s[1:],p)));
        else:
            return first_match and self.isMatch(s[1:],p[1:])

解法二 动态规划

最终定义的二维数组。通过两层循环进行匹配。

• 从左往右扫
  • 字符后面是否跟着星号会影响结果，分析起来有点复杂。
    
• 从右往左扫描
  • 星号的前面肯定有一个字符，星号也只影响这一个字符，它就像一个拷贝器。
    
  • s、p 串是否匹配，取决于：最右端是否匹配、剩余的子串是否匹配。
  • 只是最右端可能是特殊符号，需要分情况讨论而已。
• 通用地表示出子问题
  • 大子串是否匹配，和剩余子串是否匹配，是规模不一样的同一问题。
    
• 情况1：s[i-1]s[i−1] 和 p[j-1]p[j−1] 是匹配的
  • 最右端的字符是匹配的，那么，大问题的答案 = 剩余子串是否匹配。
    
• 情况2：s[i-1]s[i−1] 和 p[j-1]p[j−1] 是不匹配的
  • 右端不匹配，还不能判死刑——可能是 p[j-1]p[j−1] 为星号造成的不匹配，星号不是真实字符，它不匹配不算数。
  • 如果 p[j-1]p[j−1] 不是星号，那就真的不匹配了。
    

p[j-1]=="*"，且 s[i−1] 和 p[j−2] 匹配

• p[j-1] 是星号，并且 s[i−1] 和 p[j−2] 匹配，要考虑三种情况：
  • p[j−1] 星号可以让 p[j−2] 在 p 串中消失、出现 1 次、出现 >=2 次。
  • 只要其中一种使得剩余子串能匹配，那就能匹配，见下图 a1、a2、a3。
    
  • a3 情况：假设 s 的右端是一个 a，p 的右端是 a * ，* 让 a 重复 >= 2 次
    • 星号不是真实字符，s、p是否匹配，要看 s 去掉末尾的 a，p 去掉末尾一个 a，剩下的是否匹配。
    • 星号拷贝了 >=2 个 a，拿掉一个，剩下 >=1 个a，p 末端依旧是 a* 没变。
    • s 末尾的 a 被抵消了，继续考察 s(0,i-2) 和 p(0,i-1) 是否匹配。

p[j-1]=="*"，但 s[i−1] 和 p[j−2] 不匹配

• s[i-1]和p[j−2] 不匹配，还有救，p[j−1] 星号可以干掉 p[j−2]，继续考察 s(0,i−1) 和 p(0,j−3)。
  

base case

• p为空串，s不为空串，肯定不匹配。
• s为空串，但p不为空串，要想匹配，只可能是右端是星号，它干掉一个字符后，把 p 变为空串。
• s、p都为空串，肯定匹配。
  

代码如下：

 public class Regular_Expression_Matching2 {
    	public static boolean isMatch(String text, String pattern) {
    	    // 多一维的空间，因为求 dp[len - 1][j] 的时候需要知道 dp[len][j] 的情况，
    	    // 多一维的话，就可以把 对 dp[len - 1][j] 也写进循环了
    	    boolean[][] dp = new boolean[text.length() + 1][pattern.length() + 1];//定义4行六列数组
    	    // dp[len][len] 代表两个空串是否匹配了，"" 和 "" ，当然是 true 了。
    	    dp[text.length()][pattern.length()] = true;
    
    	    // 从 len 开始减少
    	    for (int i = text.length(); i >= 0; i--) {
    	        for (int j = pattern.length(); j >= 0; j--) {
    	            // dp[text.length()][pattern.length()] 已经进行了初始化
    	            if(i==text.length()&&j==pattern.length()) continue;
    
    	            boolean first_match = (i < text.length() && j < pattern.length()
    	            		
    	                && (pattern.charAt(j) == text.charAt(i) || pattern.charAt(j) == '.'));
    	            if (j + 1 < pattern.length() && pattern.charAt(j + 1) == '*') {
    	                dp[i][j] = dp[i][j + 2] || first_match && dp[i + 1][j];//先计算与运算，再计算或运算
    	            } else {
    	                dp[i][j] = first_match && dp[i + 1][j + 1];
    	            }
    	        }
    	    }
    	    return dp[0][0];
    	}
    	public static void main(String args[]) {
    		String text="aab";
    		String pattern="c*a*b";
    		boolean ans=isMatch(text,pattern);
    		System.out.println(ans);
    	}
    }

时间复杂度：假设 text 的长度是 T，pattern 的长度是 P ，空间复杂度就是 O（TP）。
空间复杂度：申请了 dp 空间，所以是 O（TP）。

对应python代码如下：

class Solution(object):
    def isMatch(self, s, p):
        dp = [[False] * (len(p) + 1) for _ in range(len(s) + 1)]
        dp[len(s)][len(p)]=True

        for i in range(len(s),-1,-1):
            for j in range(len(p),-1,-1):
                if(i == len(s) and j == len(p)):
                    continue
                first_match = (i < len(s) and j < len(p) and 
                             (p[j] == s[i] or p[j] == '.'))
                if (j + 1 < len(p) and p[j+1] == '*'):
                    dp[i][j] = dp[i][j+2] or (first_match and dp[i+1][j])
                else:
                    dp[i][j]=first_match and dp[i+1][j+1]
        return dp[0][0]

参考文献

• https://zhuanlan.zhihu.com/p/55996091
• https://leetcode-cn.com/problems/regular-expression-matching/solution