0x00 前言
在之前介绍的梯度下降法的步骤中,在每次更新参数时是需要计算所有样本的,通过对整个数据集的所有样本的计算来求解梯度的方向。这种计算方法被称为:批量梯度下降法BGD(Batch Gradient Descent)。但是这种方法在数据量很大时需要计算很久。
针对该缺点,有一种更好的方法:随机梯度下降法SGD(stochastic gradient descent),随机梯度下降是每次迭代使用一个样本来对参数进行更新。虽然不是每次迭代得到的损失函数都向着全局最优方向,但是大的整体的方向是向全局最优解的,最终的结果往往是在全局最优解附近。但是相比于批量梯度,这样的方法更快,我们也是可以接受的。下面就来学学随机梯度下降法吧!
0x01 理解随机梯度下降
1.1 随机取值的公式推导
批量梯度下降法,每一次计算过程,都要将样本中所有信息进行批量计算。但是显然如果样本量很大的话,计算梯度就比较耗时。基于这个问题,改进的方案就是随机梯度下降法。即每次迭代随机选取一个样本来对参数进行更新。使得训练速度加快。
下面我们从数学的角度来看:我们将原本的矩阵中根据样本数量求和这一操作去掉,同样也就不需要除以m了。
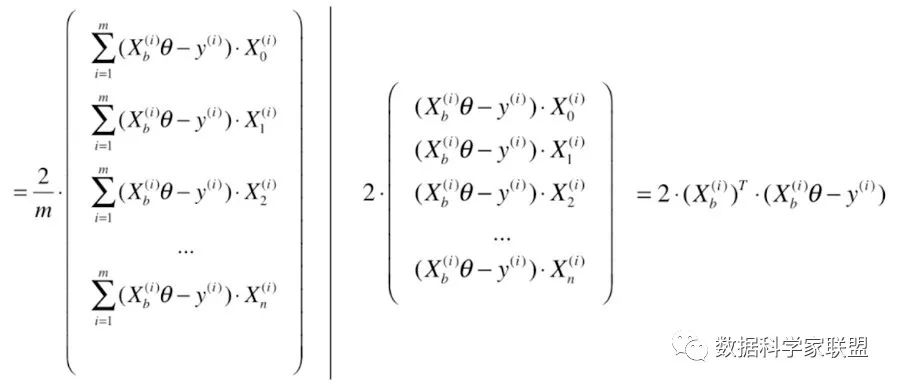
最终我们得到损失函数的进行求导,得到的结果为:
要注意,得到的向量是搜索方向,不是梯度方向,因此已经不是算是函数的梯度了。
1.2 随机下降与学习率的取值
其过程就是:每次随机取出一个i,得到一个向量,沿着这个随机产生的向量的方向进行搜索,不停的迭代,得到的损失函数的最小值。
随机梯度下降法的搜索过程如下图所示。如果是批量搜索,那么每次都是沿着一个方向前进,但是随机梯度下降法由于不能保证随机选择的方向是损失函数减小的方向,更不能保证一定是减小速度最快的方向,所以搜索路径就会呈现下图的态势。即随机梯度下降有着不可预知性。
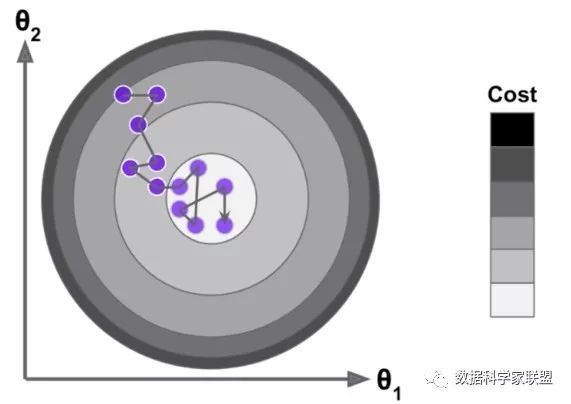
但实验结论告诉我们,通过随机梯度下降法,依然能够达到最小值的附近(用精度换速度)。
随机





 本文介绍了随机梯度下降法(SGD)的优势和原理,包括随机取值的公式推导和学习率的设计。相较于批量梯度下降(BGD),SGD在大数据集上速度更快,尽管其搜索路径具有不可预知性,但通过适当调整学习率,仍能接近全局最优解。文中还对比了BGD和SGD在运行时间、迭代次数上的表现,并提供了代码实现,包括学习率的改进策略和sklearn库中的SGD实现。
本文介绍了随机梯度下降法(SGD)的优势和原理,包括随机取值的公式推导和学习率的设计。相较于批量梯度下降(BGD),SGD在大数据集上速度更快,尽管其搜索路径具有不可预知性,但通过适当调整学习率,仍能接近全局最优解。文中还对比了BGD和SGD在运行时间、迭代次数上的表现,并提供了代码实现,包括学习率的改进策略和sklearn库中的SGD实现。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 1271
1271

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








