经典C语言算法源码合集与实战解析

本文还有配套的精品资源，点击获取

简介：该资源包含近200个经典C语言源码，专注于算法的设计与实现，是深入学习C语言和算法的宝贵资料。内容涵盖基础语法、指针操作、数据结构、排序查找、递归与动态规划等核心技术，适用于算法爱好者、编程学习者及项目开发人员。通过实际源码分析与练习，学习者可全面提升C语言编程能力与算法思维，为开发高性能系统级应用打下坚实基础。

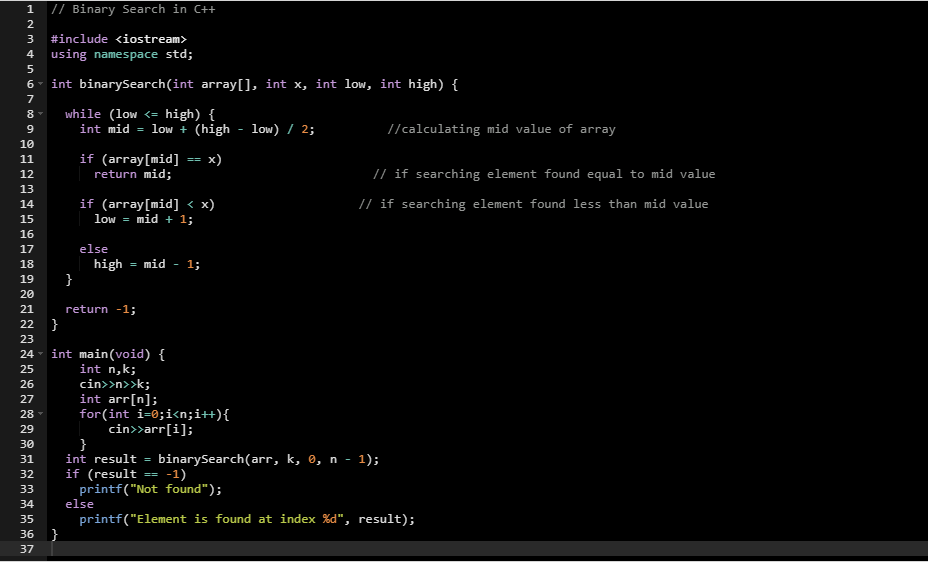
1. C语言基础语法与算法入门

C语言作为一门经典而强大的编程语言，广泛应用于系统编程、嵌入式开发和算法实现。本章将从C语言的基本语法入手，介绍变量、数据类型、运算符、流程控制结构等基础内容，并简要说明算法在C语言编程中的重要地位，为后续章节打下坚实基础。

1.1 C语言的基本结构与编程范式

C语言是一种静态类型、面向过程的编程语言，程序由函数组成，主函数 main() 是程序的入口。一个最简单的C语言程序结构如下：

#include <stdio.h>  // 引入标准输入输出头文件

int main() {
    printf("Hello, World!\n");  // 输出字符串
    return 0;  // 返回0表示程序正常结束
}

代码解释：

• #include <stdio.h> ：预处理指令，用于引入标准输入输出库函数。
• int main() ：主函数，每个C程序必须有且仅有一个主函数。
• printf() ：标准库函数，用于在控制台输出信息。
• return 0; ：返回值，0表示程序成功执行并结束。

编程范式说明：

C语言采用 过程式编程 （Procedural Programming），强调函数的划分和流程控制。其核心思想是将程序拆解为多个函数模块，每个函数完成特定任务。这种结构有助于代码重用和逻辑清晰。

编译与运行流程：

1. 使用文本编辑器编写 .c 源文件；
2. 使用C编译器（如 GCC）进行编译：
   bash gcc hello.c -o hello
3. 运行生成的可执行文件：
   bash ./hello

总结：

掌握C语言的基础语法结构是进一步学习指针、数据结构与算法的前提。下一节将深入讲解变量与数据类型的基本概念及其使用方法。

2. 指针与内存管理的核心机制

2.1 指针的基本概念与声明

2.1.1 指针变量的定义与初始化

在C语言中，指针是一种特殊的变量类型，用于存储内存地址。指针的定义方式如下：

数据类型 *指针变量名;

例如：

int *p;
float *q;
char *r;

上述代码分别定义了一个指向整型、浮点型和字符型的指针变量。指针变量并不直接存储数据值，而是存储数据所在的内存地址。

指针变量在定义后，必须进行初始化，否则其值为一个“野指针”（wild pointer），指向一个不可预测的地址。初始化的方式可以是将某个变量的地址赋给指针：

int a = 10;
int *p = &a; // & 是取地址运算符

也可以将指针初始化为 NULL，表示当前不指向任何有效地址：

int *p = NULL;

NULL 通常定义为整型常量 0，表示空指针。在使用前应判断指针是否为 NULL，以避免访问非法地址。

2.1.2 指针与变量地址的关系

每个变量在内存中都有唯一的地址，使用 & 运算符可以获取变量的地址。例如：

#include <stdio.h>

int main() {
    int a = 20;
    int *p = &a;

    printf("变量a的地址：%p\n", &a);
    printf("指针p的值（即a的地址）：%p\n", p);
    return 0;
}

输出结果类似于：

变量a的地址：0x7fff5fbff8ac
指针p的值（即a的地址）：0x7fff5fbff8ac

从上述代码可以看出， p 存储的就是变量 a 的内存地址。通过指针访问变量的值，可以使用 * 运算符（解引用）：

printf("a的值：%d\n", *p);

这将输出 20 ，表示通过指针访问了变量 a 的值。

2.2 指针的运算与操作

2.2.1 指针的加减操作

指针的加减操作并不是简单的数值加减，而是基于所指向数据类型的大小进行调整。例如，对于一个 int *p ，在32位系统中， int 占4字节，因此 p+1 表示向后移动4字节。

#include <stdio.h>

int main() {
    int arr[] = {10, 20, 30, 40};
    int *p = arr;

    printf("arr[0] 的地址：%p\n", &arr[0]);
    printf("arr[1] 的地址：%p\n", &arr[1]);
    printf("p 的值：%p\n", p);
    printf("p+1 的值：%p\n", p+1);
    return 0;
}

输出结果类似于：

arr[0] 的地址：0x7fff5fbff8a0
arr[1] 的地址：0x7fff5fbff8a4
p 的值：0x7fff5fbff8a0
p+1 的值：0x7fff5fbff8a4

可以看出， p+1 向后偏移了4个字节，即一个 int 类型的大小。这种机制使得指针可以方便地遍历数组。

2.2.2 指针的比较与引用

指针之间可以进行比较操作，常用于判断两个指针是否指向同一内存地址或用于数组边界判断。

#include <stdio.h>

int main() {
    int arr[] = {10, 20, 30, 40};
    int *p = &arr[0];
    int *q = &arr[2];

    if (p < q) {
        printf("p 指向的地址在 q 之前\n");
    }

    // 引用指针值
    printf("p 指向的值：%d\n", *p);
    printf("q 指向的值：%d\n", *q);

    return 0;
}

输出：

p 指向的地址在 q 之前
p 指向的值：10
q 指向的值：30

指针比较的前提是它们指向同一数组或对象。如果比较不同数组的指针，结果是未定义行为。

2.3 内存管理与访问控制

2.3.1 栈内存与堆内存的区别

在C语言中，内存主要分为两种类型：栈（stack）和堆（heap）。

类型	特点	使用方式	生命周期
栈内存	自动分配与释放	函数调用时自动分配，函数返回后释放	临时变量的生命周期
堆内存	手动分配与释放	使用 malloc 、 calloc 、 realloc 和 free	由程序员控制释放

示例代码如下：

#include <stdio.h>
#include <stdlib.h>

int main() {
    // 栈内存
    int a = 10;
    int arr[5] = {1, 2, 3, 4, 5};

    // 堆内存
    int *p = (int *)malloc(5 * sizeof(int));
    if (p == NULL) {
        printf("内存分配失败\n");
        return 1;
    }

    for (int i = 0; i < 5; i++) {
        p[i] = i * 10;
    }

    for (int i = 0; i < 5; i++) {
        printf("%d ", p[i]);
    }

    free(p); // 释放堆内存
    return 0;
}

输出：

0 10 20 30 40

栈内存适用于生命周期短、大小固定的数据，而堆内存则用于需要长期存在或大小动态变化的数据。

2.3.2 指针与数组的关系

在C语言中，数组名本质上是一个指向数组首元素的指针。例如：

int arr[] = {10, 20, 30};
int *p = arr; // 等价于 int *p = &arr[0];

可以通过指针访问数组元素：

printf("arr[0] = %d\n", *p);     // 输出 10
printf("arr[1] = %d\n", *(p+1)); // 输出 20

数组和指针之间的关系也可以用流程图表示：

graph TD
    A[数组arr] --> B[地址 &arr[0]]
    B --> C[指针p]
    C --> D[访问arr[0]]
    C --> E[访问arr[1]]
    C --> F[访问arr[2]]

2.3.3 指针的非法访问与调试技巧

指针的非法访问通常包括以下几种情况：

1. 野指针 ：未初始化的指针。
2. 空指针解引用 ：访问 NULL 指针。
3. 越界访问 ：访问超出数组范围的地址。
4. 释放后使用 ：使用已经被 free 释放的指针。

调试指针问题的常用方法包括：

• 使用断言（ assert(p != NULL) ）检查指针有效性。
• 使用调试器（如 GDB）逐行执行，查看指针值变化。
• 利用 Valgrind 工具检测内存泄漏与非法访问。

示例代码演示非法访问：

#include <stdio.h>

int main() {
    int *p;
    *p = 100; // 野指针，非法访问
    return 0;
}

该程序在运行时可能崩溃或产生不可预测的结果。

正确做法应为：

int a;
int *p = &a;
*p = 100;

或：

int *p = (int *)malloc(sizeof(int));
if (p != NULL) {
    *p = 100;
    free(p);
}

通过合理初始化和释放，可以有效避免指针相关的内存错误。

3. 数据结构在C语言中的实现

数据结构是计算机科学中最基础也是最核心的内容之一。它不仅是算法实现的基础，更是构建复杂系统和优化程序性能的关键。C语言作为一门贴近底层、高效灵活的编程语言，非常适合用于实现各种数据结构，并通过内存管理的直接操作来提升程序效率。

本章将从线性结构入手，逐步深入到树和图结构的实现，并最终对各种数据结构在不同场景下的性能进行分析。通过本章的学习，读者将掌握如何在C语言中构建链表、栈、队列、二叉树、图等常见数据结构，并理解其背后的内存操作机制和算法复杂度特性。

3.1 线性结构的实现与应用

线性结构是最基础也是最常用的数据结构类型，其特点是数据元素之间存在一对一的线性关系。常见的线性结构包括数组、链表、栈和队列。在C语言中，这些结构可以通过指针、数组以及结构体进行灵活实现。

3.1.1 链表的创建与遍历

链表是一种动态数据结构，由一系列节点组成，每个节点包含数据和指向下一个节点的指针。与数组相比，链表的优势在于可以动态分配内存，避免固定大小的限制。

链表节点的定义

typedef struct Node {
    int data;
    struct Node* next;
} Node;

参数说明：
- data ：存储节点的数据。
- next ：指向下一个节点的指针。

链表的创建与插入

Node* create_node(int data) {
    Node* new_node = (Node*)malloc(sizeof(Node));
    if (!new_node) {
        printf("Memory allocation failed.\n");
        return NULL;
    }
    new_node->data = data;
    new_node->next = NULL;
    return new_node;
}

void insert_at_end(Node** head, int data) {
    Node* new_node = create_node(data);
    if (*head == NULL) {
        *head = new_node;
        return;
    }
    Node* temp = *head;
    while (temp->next != NULL) {
        temp = temp->next;
    }
    temp->next = new_node;
}

代码逻辑分析：
- create_node 函数用于创建一个新的节点，并初始化其数据和指针。
- insert_at_end 函数用于在链表末尾插入新节点：
- 如果链表为空，则将新节点设为头节点；
- 否则，遍历链表直到末尾，将新节点连接到链表尾部。

链表的遍历

void traverse_list(Node* head) {
    Node* current = head;
    while (current != NULL) {
        printf("%d -> ", current->data);
        current = current->next;
    }
    printf("NULL\n");
}

逻辑说明：
- 从头节点开始，逐个访问每个节点的 data 字段，直到 next 为 NULL 为止。

示例代码运行

int main() {
    Node* head = NULL;
    insert_at_end(&head, 10);
    insert_at_end(&head, 20);
    insert_at_end(&head, 30);
    traverse_list(head);
    return 0;
}

输出结果：

10 -> 20 -> 30 -> NULL

3.1.2 栈与队列的数组与链式实现

栈和队列是两种重要的线性结构，分别遵循后进先出（LIFO）和先进先出（FIFO）原则。

栈的数组实现

#define MAX_SIZE 100

typedef struct {
    int items[MAX_SIZE];
    int top;
} Stack;

void push(Stack* s, int value) {
    if (s->top == MAX_SIZE - 1) {
        printf("Stack overflow.\n");
        return;
    }
    s->items[++s->top] = value;
}

int pop(Stack* s) {
    if (s->top == -1) {
        printf("Stack underflow.\n");
        return -1;
    }
    return s->items[s->top--];
}

参数说明：
- MAX_SIZE ：栈的最大容量。
- items ：数组用于存储栈元素。
- top ：栈顶指针，初始为-1表示空栈。

栈的链式实现（部分代码）

typedef struct StackNode {
    int data;
    struct StackNode* next;
} StackNode;

void push_linked(StackNode** top, int data) {
    StackNode* new_node = (StackNode*)malloc(sizeof(StackNode));
    if (!new_node) return;
    new_node->data = data;
    new_node->next = *top;
    *top = new_node;
}

逻辑说明：
- 使用链表实现栈，每次插入节点到链表头部，模拟栈顶压入操作。

队列的链式实现（核心结构）

typedef struct QueueNode {
    int data;
    struct QueueNode* next;
} QueueNode;

typedef struct {
    QueueNode* front;
    QueueNode* rear;
} Queue;

void enqueue(Queue* q, int data) {
    QueueNode* new_node = (QueueNode*)malloc(sizeof(QueueNode));
    if (!new_node) return;
    new_node->data = data;
    new_node->next = NULL;
    if (q->rear == NULL) {
        q->front = q->rear = new_node;
    } else {
        q->rear->next = new_node;
        q->rear = new_node;
    }
}

逻辑说明：
- 使用链表实现队列，维护 front 和 rear 指针，保证先进先出的操作。

3.2 树与图结构的构建

树和图是典型的非线性结构，适用于表达复杂的数据关系，如文件系统、社交网络、决策树等。

3.2.1 二叉树的定义与遍历

二叉树是每个节点最多有两个子节点的树结构，通常称为左子节点和右子节点。

二叉树节点定义

typedef struct TreeNode {
    int data;
    struct TreeNode* left;
    struct TreeNode* right;
} TreeNode;

创建二叉树节点

TreeNode* create_tree_node(int data) {
    TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
    node->data = data;
    node->left = node->right = NULL;
    return node;
}

前序遍历（递归实现）

void preorder(TreeNode* root) {
    if (root == NULL) return;
    printf("%d ", root->data);
    preorder(root->left);
    preorder(root->right);
}

逻辑说明：
- 先访问根节点，再递归访问左子树，最后访问右子树。

示例构建与遍历

int main() {
    TreeNode* root = create_tree_node(1);
    root->left = create_tree_node(2);
    root->right = create_tree_node(3);
    root->left->left = create_tree_node(4);
    root->left->right = create_tree_node(5);

    printf("Preorder traversal: ");
    preorder(root);
    return 0;
}

输出结果：

Preorder traversal: 1 2 4 5 3

3.2.2 图的邻接表与邻接矩阵实现

图由顶点和边组成，可以使用邻接表或邻接矩阵来表示。

邻接表实现

typedef struct AdjListNode {
    int dest;
    struct AdjListNode* next;
} AdjListNode;

typedef struct AdjList {
    AdjListNode* head;
} AdjList;

typedef struct Graph {
    int num_vertices;
    AdjList* array;
} Graph;

Graph* create_graph(int vertices) {
    Graph* graph = (Graph*)malloc(sizeof(Graph));
    graph->num_vertices = vertices;
    graph->array = (AdjList*)malloc(vertices * sizeof(AdjList));
    for (int i = 0; i < vertices; ++i)
        graph->array[i].head = NULL;
    return graph;
}

void add_edge(Graph* graph, int src, int dest) {
    AdjListNode* new_node = (AdjListNode*)malloc(sizeof(AdjListNode));
    new_node->dest = dest;
    new_node->next = graph->array[src].head;
    graph->array[src].head = new_node;
}

结构说明：
- AdjListNode ：邻接表中的节点，表示边的目标顶点。
- AdjList ：邻接表的数组元素，每个元素是一个链表。
- Graph ：整个图的结构，包含顶点数量和邻接表数组。

邻接矩阵实现（部分结构）

#define MAX_VERTICES 100

typedef struct {
    int matrix[MAX_VERTICES][MAX_VERTICES];
    int num_vertices;
} GraphMatrix;

void add_edge_matrix(GraphMatrix* g, int u, int v) {
    g->matrix[u][v] = 1;
    g->matrix[v][u] = 1; // 无向图
}

结构说明：
- 使用二维数组表示图的连接关系，适合顶点数量固定的场景。

性能对比表格：

实现方式	优点	缺点	适用场景
邻接表	空间效率高，适合稀疏图	遍历边时效率较低	大型图、动态图
邻接矩阵	查询边是否存在效率高（O(1)）	空间复杂度高 O(n²)，适合顶点数少的图	小型图、密集图

3.3 常用数据结构的算法性能分析

为了选择合适的数据结构应对不同场景，我们需要对其时间复杂度和空间复杂度进行分析。

3.3.1 时间复杂度与空间复杂度评估

数据结构	插入操作	删除操作	查找操作	空间复杂度
链表	O(1)	O(1)	O(n)	O(n)
栈（数组）	O(1)	O(1)	O(1)	O(n)
队列（链表）	O(1)	O(1)	O(1)	O(n)
二叉树（平衡）	O(logn)	O(logn)	O(logn)	O(n)
图（邻接表）	O(1)	O(1)	O(n)	O(V + E)
图（邻接矩阵）	O(1)	O(1)	O(1)	O(V²)

3.3.2 不同数据结构的适用场景对比

场景描述	推荐数据结构	原因说明
存储动态增长的集合	链表	支持动态内存分配，插入删除高效
表达函数调用栈	栈（数组）	LIFO 特性天然匹配函数调用机制
任务调度（先进先出）	队列（链表）	FIFO 机制天然匹配任务调度需求
搜索树结构，快速查找	平衡二叉树（如 AVL）	插入、删除、查找均为 O(logn)
社交网络、地图路径分析	图（邻接表）	支持稀疏连接，便于遍历邻接节点
游戏AI决策树（状态快速切换）	图（邻接矩阵）	快速判断状态是否可达，便于剪枝操作

Mermaid 流程图：数据结构选择流程图

graph TD
    A[开始选择数据结构] --> B{是否需要频繁插入/删除?}
    B -->|是| C[链表]
    B -->|否| D{是否需要顺序访问?}
    D -->|是| E[数组]
    D -->|否| F{是否需要LIFO访问?}
    F -->|是| G[栈]
    F -->|否| H{是否需要FIFO访问?}
    H -->|是| I[队列]
    H -->|否| J{是否涉及图结构?}
    J -->|是| K[图结构]
    J -->|否| L[树结构]

通过本章的深入学习，读者已经掌握了C语言中常见的线性结构、树和图结构的实现方式，并了解了它们在不同场景下的性能差异。这些知识将为后续章节中更复杂的算法设计与优化打下坚实的基础。

4. 排序与查找算法的C语言实现

排序与查找是算法中最基础也是最常用的两类操作。在C语言中，理解并掌握这些算法的实现方式，不仅能提升代码效率，还能加深对内存操作、递归调用和性能分析的理解。本章将从基础排序算法入手，逐步过渡到高效排序与查找算法，并深入分析其时间复杂度、空间复杂度及适用场景。

4.1 排序算法详解与实现

排序是将一组数据按照某种顺序（如升序或降序）排列的过程。在C语言中，常见的排序算法包括冒泡排序、选择排序、快速排序、归并排序等。这些算法在不同数据规模和数据特性下表现各异，选择合适的排序方法对于程序性能至关重要。

4.1.1 冒泡排序与选择排序的实现与优化

冒泡排序是一种基础但效率较低的排序算法，其基本思想是通过相邻元素的比较和交换来将较大的元素逐渐“浮”到数组末尾。选择排序则通过每次从未排序部分中选择最小（或最大）元素，放到已排序部分的末尾。

冒泡排序实现

void bubble_sort(int arr[], int n) {
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                // 交换 arr[j] 和 arr[j+1]
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

逐行解读：

• 第2行：外层循环控制排序的轮数，共进行 n-1 次。
• 第4行：内层循环负责比较相邻元素，共进行 n-i-1 次，随着排序进行，最后几个元素已排好序，无需再比较。
• 第5行：比较当前元素与下一个元素，若顺序错误则交换。
• 第6~9行：完成交换操作。

冒泡排序优化：

若某一轮没有发生任何交换，说明数组已经有序，可以提前终止。

void optimized_bubble_sort(int arr[], int n) {
    for (int i = 0; i < n - 1; i++) {
        int swapped = 0;
        for (int j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
                swapped = 1;
            }
        }
        if (!swapped) break;
    }
}

选择排序实现

void selection_sort(int arr[], int n) {
    for (int i = 0; i < n - 1; i++) {
        int min_index = i;
        for (int j = i + 1; j < n; j++) {
            if (arr[j] < arr[min_index]) {
                min_index = j;
            }
        }
        // 交换最小值和当前元素
        int temp = arr[min_index];
        arr[min_index] = arr[i];
        arr[i] = temp;
    }
}

逐行解读：

• 第2行：外层循环遍历数组元素。
• 第4行：假设当前元素为最小值。
• 第5~8行：遍历未排序部分，寻找最小值的索引。
• 第10~13行：交换当前元素与找到的最小值。

性能对比：

算法	时间复杂度（平均）	时间复杂度（最坏）	是否稳定排序	空间复杂度
冒泡排序	O(n²)	O(n²)	是	O(1)
选择排序	O(n²)	O(n²)	否	O(1)

结论： 冒泡排序适合教学和小数据集排序，选择排序在移动次数少的场景中表现更好。

4.1.2 快速排序与归并排序的递归实现

当数据量较大时，冒泡和选择排序的效率就显得不足。此时，快速排序和归并排序是更优的选择。

快速排序实现

快速排序基于分治思想，选取一个基准元素（pivot），将数组划分为两个子数组：小于等于 pivot 的元素和大于 pivot 的元素，然后递归地对两个子数组排序。

int partition(int arr[], int low, int high) {
    int pivot = arr[high]; // 选择最后一个元素为基准
    int i = low - 1;       // i 表示小于 pivot 的区域的最后一个索引

    for (int j = low; j < high; j++) {
        if (arr[j] <= pivot) {
            i++;
            // 交换 arr[i] 和 arr[j]
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }
    // 将 pivot 放到正确的位置
    int temp = arr[i + 1];
    arr[i + 1] = arr[high];
    arr[high] = temp;
    return i + 1;
}

void quick_sort(int arr[], int low, int high) {
    if (low < high) {
        int pi = partition(arr, low, high);
        quick_sort(arr, low, pi - 1);  // 递归左半部分
        quick_sort(arr, pi + 1, high); // 递归右半部分
    }
}

逻辑分析：

• partition 函数负责将数组分区，并返回 pivot 的最终位置。
• quick_sort 递归地对左右子数组进行排序。

时间复杂度分析：

• 最好情况：O(n log n)
• 平均情况：O(n log n)
• 最坏情况（已排序数组）：O(n²)

归并排序实现

归并排序同样采用分治策略，将数组分成两半，分别排序后再合并。

void merge(int arr[], int l, int m, int r) {
    int n1 = m - l + 1;
    int n2 = r - m;

    // 创建临时数组
    int L[n1], R[n2];

    // 拷贝数据到临时数组
    for (int i = 0; i < n1; i++)
        L[i] = arr[l + i];
    for (int j = 0; j < n2; j++)
        R[j] = arr[m + 1 + j];

    // 合并两个子数组
    int i = 0, j = 0, k = l;
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    // 拷贝剩余元素
    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }
    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}

void merge_sort(int arr[], int l, int r) {
    if (l < r) {
        int m = l + (r - l) / 2;
        merge_sort(arr, l, m);
        merge_sort(arr, m + 1, r);
        merge(arr, l, m, r);
    }
}

逻辑分析：

• merge 函数负责将两个已排序子数组合并成一个有序数组。
• merge_sort 递归地将数组一分为二，直到子数组长度为1，然后进行合并。

时间复杂度分析：

• 最好、平均、最坏情况均为 O(n log n)

快速排序与归并排序对比

特性	快速排序	归并排序
时间复杂度	O(n log n)	O(n log n)
空间复杂度	O(log n)	O(n)
是否稳定排序	否	是
适用场景	大数据量排序	需要稳定排序

mermaid流程图：

graph TD
    A[快速排序] --> B[选择pivot]
    B --> C{比较并分区}
    C --> D[递归排序左半部]
    C --> E[递归排序右半部]
    A --> F[排序完成]
    G[归并排序] --> H[拆分数组]
    H --> I{递归拆分}
    I --> J[排序子数组]
    J --> K[合并两个有序数组]
    G --> L[排序完成]

4.2 查找算法的实现与应用

查找是在数据集中寻找特定元素的过程。常见的查找算法有线性查找、二分查找、哈希查找等。

4.2.1 线性查找与二分查找的比较

线性查找实现

线性查找适用于无序数组，逐个比较元素。

int linear_search(int arr[], int n, int target) {
    for (int i = 0; i < n; i++) {
        if (arr[i] == target) {
            return i;
        }
    }
    return -1;
}

分析：

• 时间复杂度：O(n)
• 适用于小数据量或无序数据

二分查找实现

二分查找适用于有序数组，每次将查找范围缩小一半。

int binary_search(int arr[], int left, int right, int target) {
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (arr[mid] == target)
            return mid;
        if (arr[mid] < target)
            left = mid + 1;
        else
            right = mid - 1;
    }
    return -1;
}

分析：

• 时间复杂度：O(log n)
• 适用于大数据量的有序查找

性能对比表格

查找方式	数据要求	时间复杂度	适用场景
线性查找	无序或有序	O(n)	小数据或无序集合
二分查找	必须有序	O(log n)	大数据、有序集合查找

4.2.2 哈希查找与冲突解决策略

哈希查找通过哈希函数将元素映射到表中的一个位置来访问记录，实现快速查找。

哈希表结构定义

#define TABLE_SIZE 100

typedef struct {
    int key;
    int value;
} HashItem;

HashItem* hash_table[TABLE_SIZE];

unsigned int hash_function(int key) {
    return key % TABLE_SIZE;
}

插入与查找实现

void insert(int key, int value) {
    unsigned int index = hash_function(key);
    HashItem* item = (HashItem*)malloc(sizeof(HashItem));
    item->key = key;
    item->value = value;

    // 简单线性探测解决冲突
    while (hash_table[index] != NULL && hash_table[index]->key != key) {
        index = (index + 1) % TABLE_SIZE;
    }
    hash_table[index] = item;
}

int search(int key) {
    unsigned int index = hash_function(key);
    while (hash_table[index] != NULL) {
        if (hash_table[index]->key == key)
            return hash_table[index]->value;
        index = (index + 1) % TABLE_SIZE;
    }
    return -1;
}

冲突解决策略：

• 线性探测法： 发生冲突时向后查找下一个空位。
• 链地址法： 每个哈希桶维护一个链表，存储冲突的元素。

哈希查找性能分析

查找方式	平均时间复杂度	最坏时间复杂度	说明
哈希查找	O(1)	O(n)	需合理设计哈希函数和冲突解决策略

4.3 算法性能对比与优化技巧

在实际编程中，面对不同规模的数据和不同的应用场景，如何选择合适的排序与查找算法至关重要。

4.3.1 大数据量下的算法选择

数据规模	推荐排序算法	推荐查找算法
小数据（<100）	冒泡排序、插入排序	线性查找
中等数据（100~1000）	快速排序、归并排序	二分查找
大数据（>1000）	快速排序、堆排序	哈希查找

4.3.2 算法优化的常用方法与注意事项

• 预排序： 对数据进行一次排序后，后续查找效率更高。
• 避免重复计算： 如哈希查找中缓存哈希值。
• 减少交换次数： 在排序中尽量减少不必要的数据交换。
• 内存优化： 对于归并排序等需要辅助空间的算法，应合理分配内存。

优化建议：

• 使用快速排序时，可以随机选择 pivot 以避免最坏情况。
• 使用二分查找前，确保数组已排序。
• 哈希查找应设计良好的哈希函数，避免冲突过多。

mermaid流程图：

graph LR
    A[排序算法选择] --> B{数据规模}
    B -->|小数据| C[冒泡/插入排序]
    B -->|中等数据| D[快速/归并排序]
    B -->|大数据| E[快速/堆排序]
    F[查找算法选择] --> G{数据是否有序}
    G -->|有序| H[二分查找]
    G -->|无序| I[线性查找]
    F --> J{是否需要高速查找}
    J -->|是| K[哈希查找]

5. 递归与分治策略的编程实践

递归与分治是算法设计中极为关键的两种思想。递归通过函数调用自身实现问题的分解与求解，而分治法则将问题划分为若干个子问题分别解决，最终合并结果。本章将从递归函数的基本原理出发，深入讲解其调用机制、递归终止条件的设计，并结合分治思想，通过快速排序、归并排序等经典算法的实现，帮助读者掌握如何在C语言中编写高效且安全的递归程序。

5.1 递归函数的调用机制与实现原理

5.1.1 递归的基本概念与结构特征

递归是一种函数直接或间接调用自己的编程方式。一个典型的递归函数通常包含两个部分：

• 递归终止条件（Base Case） ：防止无限递归，是递归的出口。
• 递归步骤（Recursive Step） ：将问题分解为更小的子问题，并调用自身进行求解。

例如，阶乘函数 n! 可以用递归表示为：

int factorial(int n) {
    if (n == 0) return 1;     // Base case
    else return n * factorial(n - 1); // Recursive step
}

该函数通过不断调用自身，直到 n == 0 时返回 1，从而逐步计算出 n! 。

5.1.2 函数调用栈与递归堆栈的执行流程

在C语言中，每次函数调用都会在 调用栈（Call Stack） 上分配一个新的栈帧（Stack Frame），保存局部变量、参数和返回地址等信息。递归函数的调用会导致多个栈帧的连续压栈。

例如，当调用 factorial(3) 时，调用过程如下：

factorial(3)
→ 3 * factorial(2)
    → 2 * factorial(1)
        → 1 * factorial(0)
            → return 1
        ← 1 * 1 = 1
    ← 2 * 1 = 2
← 3 * 2 = 6

通过上述流程可以看出，递归的执行顺序是 深度优先 ，即先递归调用到底层，再逐层返回计算结果。

我们可以用Mermaid流程图来描述这个过程：

graph TD
A[factorial(3)] --> B[3 * factorial(2)]
B --> C[2 * factorial(1)]
C --> D[1 * factorial(0)]
D --> E[return 1]
E --> D
D --> C
C --> B
B --> A

5.1.3 递归函数的执行效率与潜在问题

尽管递归逻辑清晰，但其执行效率通常低于迭代。主要原因包括：

• 函数调用开销 ：每次递归调用都涉及栈帧的创建与销毁。
• 栈溢出风险（Stack Overflow） ：如果递归层数过深，可能导致调用栈溢出。

例如，如果调用 factorial(-1) 而未做边界检查，函数将无限递归，最终导致栈溢出。

为避免此类问题，应确保：

1. 递归终止条件覆盖所有可能的输入。
2. 使用 尾递归优化 （Tail Recursion）或 迭代重写 来提升效率。

5.2 递归终止条件的设计与调试技巧

5.2.1 终止条件的合理设定与边界处理

递归终止条件的设计是递归函数是否正确运行的关键。常见的设计模式包括：

• 数值边界条件 ：如 n == 0 、 start > end 。
• 数据结构边界条件 ：如链表为空、数组长度为0。
• 状态转移终止条件 ：如图遍历中的节点访问终止。

例如，链表的递归遍历：

typedef struct Node {
    int data;
    struct Node* next;
} Node;

void printList(Node* head) {
    if (head == NULL) return; // Base case
    printf("%d ", head->data);
    printList(head->next); // Recursive call
}

5.2.2 递归函数的调试方法与工具使用

调试递归函数可以采用以下几种方式：

• 打印调用栈信息 ：在函数入口和出口打印参数与返回值。
• 使用调试器 ：如 GDB，设置断点查看递归调用层级。
• 可视化递归流程 ：通过日志或图表观察递归展开过程。

例如，在阶乘函数中加入调试输出：

int factorial(int n) {
    printf("Enter factorial(%d)\n", n);
    if (n == 0) {
        printf("Base case: return 1\n");
        return 1;
    }
    int result = n * factorial(n - 1);
    printf("Exit factorial(%d) -> %d\n", n, result);
    return result;
}

输出示例：

Enter factorial(3)
Enter factorial(2)
Enter factorial(1)
Enter factorial(0)
Base case: return 1
Exit factorial(1) -> 1
Exit factorial(2) -> 2
Exit factorial(3) -> 6

通过调试输出，可以清晰地看到递归函数的执行路径和返回值。

5.3 分治策略的基本思想与经典算法应用

5.3.1 分治策略的原理与实现步骤

分治（Divide and Conquer）策略的基本思想是：

1. 分解（Divide） ：将原问题划分为若干个子问题。
2. 解决（Conquer） ：递归地求解子问题。
3. 合并（Combine） ：将子问题的解合并成原问题的解。

分治策略常用于排序、查找、矩阵乘法等场景。

5.3.2 快速排序的递归实现与性能分析

快速排序是一种典型的分治算法。其基本步骤如下：

1. 选择一个基准值（pivot）。
2. 将数组划分为两部分：小于等于基准值的部分和大于基准值的部分。
3. 对左右子数组递归排序。

实现代码如下：

void quickSort(int arr[], int low, int high) {
    if (low < high) {
        int pi = partition(arr, low, high); // Partition the array
        quickSort(arr, low, pi - 1);  // Recursively sort left subarray
        quickSort(arr, pi + 1, high); // Recursively sort right subarray
    }
}

int partition(int arr[], int low, int high) {
    int pivot = arr[high]; // Select last element as pivot
    int i = low - 1;       // Index of smaller element

    for (int j = low; j < high; j++) {
        if (arr[j] <= pivot) {
            i++;
            // Swap arr[i] and arr[j]
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }
    // Swap arr[i+1] and arr[high] (or pivot)
    int temp = arr[i + 1];
    arr[i + 1] = arr[high];
    arr[high] = temp;
    return i + 1;
}

逻辑分析与参数说明：

• quickSort 是递归函数，接收数组 arr 、起始索引 low 和结束索引 high 。
• partition 函数用于将数组分为两部分，返回基准值的最终位置。
• i 用于记录小于等于 pivot 的元素位置。
• 时间复杂度：
• 最好情况：O(n log n)
• 最坏情况（已排序数组）：O(n²)
• 空间复杂度：O(log n)（递归栈）

5.3.3 归并排序的递归实现与优化建议

归并排序也是经典的分治算法，其基本步骤如下：

1. 将数组分成两半。
2. 对两半分别递归排序。
3. 将两个有序数组合并成一个有序数组。

实现代码如下：

void mergeSort(int arr[], int l, int r) {
    if (l < r) {
        int m = l + (r - l) / 2; // Avoid overflow
        mergeSort(arr, l, m);    // Sort left half
        mergeSort(arr, m + 1, r); // Sort right half
        merge(arr, l, m, r);      // Merge sorted halves
    }
}

void merge(int arr[], int l, int m, int r) {
    int n1 = m - l + 1;
    int n2 = r - m;

    int L[n1], R[n2];

    // Copy data to temp arrays
    for (int i = 0; i < n1; i++)
        L[i] = arr[l + i];
    for (int j = 0; j < n2; j++)
        R[j] = arr[m + 1 + j];

    // Merge the temp arrays back into arr[l..r]
    int i = 0, j = 0, k = l;
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    // Copy remaining elements of L[]
    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }

    // Copy remaining elements of R[]
    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}

逻辑分析与参数说明：

• mergeSort 是递归函数， l 和 r 表示数组的左右边界。
• merge 函数将两个有序子数组合并为一个有序数组。
• 使用临时数组 L 和 R 存储左右子数组，避免直接修改原数组。
• 时间复杂度：O(n log n)，空间复杂度：O(n)

性能对比与适用场景：

排序算法	最好时间复杂度	最坏时间复杂度	平均时间复杂度	是否稳定	适用场景
快速排序	O(n log n)	O(n²)	O(n log n)	否	通用排序，内存有限
归并排序	O(n log n)	O(n log n)	O(n log n)	是	大数据量排序，链表排序

5.4 递归与分治策略的综合应用实例

5.4.1 汉诺塔问题的递归实现与分析

汉诺塔问题是递归的经典应用。问题描述如下：

有三个柱子 A、B、C，A 上有 n 个盘子，盘子大小不一，大的在下，小的在上。目标是将所有盘子从 A 移动到 C，每次只能移动一个盘子，且任何时候大盘子不能在小盘子上面。

递归实现如下：

void hanoi(int n, char from, char to, char aux) {
    if (n == 1) {
        printf("Move disk 1 from %c to %c\n", from, to);
        return;
    }
    hanoi(n - 1, from, aux, to); // Move n-1 disks from from to aux
    printf("Move disk %d from %c to %c\n", n, from, to);
    hanoi(n - 1, aux, to, from); // Move n-1 disks from aux to to
}

逻辑分析：

• n == 1 是终止条件。
• 每次递归将问题规模减小为 n-1 ，先将上层盘子从 A 移动到 B，再将底层盘子移动到 C，最后将 B 上的盘子移动到 C。

该算法的时间复杂度为 O(2ⁿ)，每次递归调用将问题规模减小1，共 2ⁿ - 1 步操作。

5.4.2 矩阵乘法的分治实现（Strassen算法简述）

Strassen算法是一种分治矩阵乘法算法，其时间复杂度为 O(n^log₂7) ≈ O(n^2.81)，优于传统的 O(n³)。

其核心思想是将矩阵划分为四个子矩阵：

A = [A11 A12]
    [A21 A22]

B = [B11 B12]
    [B21 B22]

然后通过7次递归乘法计算结果矩阵 C 的四个子块。

由于实现较为复杂，这里只展示框架结构：

void strassenMultiply(int A[][N], int B[][N], int C[][N], int n) {
    if (n <= 1) {
        C[0][0] = A[0][0] * B[0][0];
        return;
    }

    // Divide matrices into submatrices
    // ...

    // Compute 7 products recursively
    // P1 = A11 * (B12 - B22)
    // P2 = (A11 + A12) * B22
    // P3 = (A21 + A22) * B11
    // P4 = A22 * (B21 - B11)
    // P5 = (A11 + A22) * (B11 + B22)
    // P6 = (A12 - A22) * (B21 + B22)
    // P7 = (A11 - A21) * (B11 + B12)

    // Combine results to compute C11, C12, C21, C22
    // ...
}

Strassen算法虽然理论复杂度较低，但由于常数因子较大，实际中在 n 较小时仍使用传统方法更高效。

5.4.3 递归与分治在实际项目中的优化策略

在实际开发中，为了提高递归与分治算法的性能，可以采取以下优化策略：

1. 尾递归优化 ：将递归调用置于函数末尾，避免栈帧累积。
2. 记忆化递归（Memoization） ：缓存中间结果，避免重复计算。
3. 迭代替代递归 ：将递归转化为循环，减少栈开销。
4. 分治算法的并行化 ：利用多线程或并行计算加速子问题求解。

例如，斐波那契数列的记忆化递归实现：

#include <stdio.h>
#include <stdlib.h>

#define MAX 100
int memo[MAX];

int fib(int n) {
    if (n <= 1) return n;
    if (memo[n] != -1) return memo[n]; // Use memoization
    memo[n] = fib(n - 1) + fib(n - 2);
    return memo[n];
}

int main() {
    for (int i = 0; i < MAX; i++) memo[i] = -1;
    printf("%d\n", fib(40));
    return 0;
}

此方法将时间复杂度从 O(2ⁿ) 降低至 O(n)，空间复杂度为 O(n)。

6. 动态规划与贪心算法的实战应用

动态规划（Dynamic Programming, DP）与贪心算法（Greedy Algorithm）是解决复杂问题的两种重要算法范式。它们广泛应用于路径规划、资源调度、组合优化等领域，尤其在解决具有重叠子问题和最优子结构的问题时表现尤为出色。本章将从理论基础出发，结合C语言的实现方式，深入解析动态规划与贪心算法的核心思想，并通过多个实战案例（如背包问题、最长公共子序列、活动选择问题等）展示其在实际项目中的应用方式与优化技巧。

6.1 动态规划的基本思想与状态转移设计

动态规划是一种将复杂问题分解为更小的子问题，并通过保存中间结果来避免重复计算的算法设计方法。其核心在于“ 最优子结构 ”和“ 重叠子问题 ”。

6.1.1 最优子结构与状态定义

最优子结构是指原问题的最优解包含子问题的最优解。例如，在“最长公共子序列”（LCS）问题中，两个序列的最长公共子序列的最优解依赖于它们的前缀子序列的最优解。

状态定义是动态规划中最关键的一步。例如，在背包问题中，我们定义状态 dp[i][w] 表示从前 i 个物品中选择，总重量不超过 w 的最大价值。

6.1.2 状态转移方程的构建

状态转移方程是动态规划的核心逻辑，它描述了如何由子问题的解推导出当前问题的解。例如，在0-1背包问题中，状态转移方程如下：

dp[i][w] = max(dp[i-1][w], dp[i-1][w - wt[i-1]] + val[i-1])

其中：
- dp[i][w] 表示从前 i 个物品中选择，总重量不超过 w 的最大价值；
- wt[i-1] 和 val[i-1] 分别表示第 i 个物品的重量和价值；
- 如果不选第 i 个物品，则结果为 dp[i-1][w] ；
- 如果选第 i 个物品，则前提是 w >= wt[i-1] ，此时结果为 dp[i-1][w - wt[i-1]] + val[i-1] 。

6.1.3 动态规划的实现步骤

1. 初始化状态数组 ：根据问题设定初始化边界条件。
2. 状态转移 ：使用状态转移方程逐步填充状态表。
3. 返回结果 ：从状态表中提取最终解。

下面是一个0-1背包问题的C语言实现：

#include <stdio.h>

int max(int a, int b) {
    return (a > b) ? a : b;
}

int knapsack(int W, int wt[], int val[], int n) {
    int dp[n+1][W+1];

    // 初始化状态表
    for (int i = 0; i <= n; i++) {
        for (int w = 0; w <= W; w++) {
            if (i == 0 || w == 0)
                dp[i][w] = 0;
            else if (wt[i-1] > w)
                dp[i][w] = dp[i-1][w];
            else
                dp[i][w] = max(val[i-1] + dp[i-1][w - wt[i-1]], dp[i-1][w]);
        }
    }

    return dp[n][W];
}

int main() {
    int val[] = {60, 100, 120};
    int wt[] = {10, 20, 30};
    int W = 50;
    int n = sizeof(val)/sizeof(val[0]);
    printf("最大价值为：%d\n", knapsack(W, wt, val, n));
    return 0;
}

代码逻辑分析 ：

• dp[i][w] 表示前 i 个物品，容量为 w 时的最大价值；
• 初始化所有 dp[0][w] 和 dp[i][0] 为 0；
• 对于每个物品 i 和容量 w ，如果当前物品的重量大于 w ，则不能选，直接继承上一层；
• 否则，取“不选”与“选”的最大值；
• 最终结果为 dp[n][W] ，即所有物品中选择，容量为 W 时的最大价值。

6.2 贪心算法的局部最优解策略

贪心算法在每一步选择中都采取当前状态下最优的选择，希望通过局部最优解达到全局最优解。它适用于具有“ 贪心选择性质 ”的问题，例如活动选择、霍夫曼编码、最小生成树的Prim算法等。

6.2.1 贪心算法的实现步骤

1. 定义问题模型 ：将问题转化为可进行贪心决策的模型；
2. 贪心选择策略 ：制定每一步的最优选择策略；
3. 最优子结构验证 ：证明贪心选择后的子问题仍然具有最优子结构；
4. 实现算法 ：根据策略编写代码。

6.2.2 活动选择问题的C语言实现

活动选择问题是一个典型的贪心问题：给定一组活动，每个活动有开始时间和结束时间，选择互不重叠的最大活动集合。

#include <stdio.h>
#include <stdlib.h>

typedef struct {
    int start;
    int end;
} Activity;

int compare(const void *a, const void *b) {
    return ((Activity*)a)->end - ((Activity*)b)->end;
}

void greedy_activity_selector(Activity activities[], int n) {
    qsort(activities, n, sizeof(Activity), compare);

    printf("选择的活动为：\n");
    printf("活动 0: 开始时间 %d, 结束时间 %d\n", activities[0].start, activities[0].end);
    int count = 1;
    int last_end = activities[0].end;

    for (int i = 1; i < n; i++) {
        if (activities[i].start >= last_end) {
            printf("活动 %d: 开始时间 %d, 结束时间 %d\n", i, activities[i].start, activities[i].end);
            last_end = activities[i].end;
            count++;
        }
    }

    printf("总共选择了 %d 个活动。\n", count);
}

int main() {
    Activity activities[] = {
        {1, 4}, {3, 5}, {0, 6}, {5, 7}, {3, 8}, {5, 9}, {6, 10}, {8, 11}
    };
    int n = sizeof(activities) / sizeof(activities[0]);

    greedy_activity_selector(activities, n);

    return 0;
}

代码逻辑分析 ：

• 将活动按结束时间升序排序，保证每次选择最早结束的活动；
• 遍历排序后的活动列表，若当前活动的开始时间大于等于上一个选中活动的结束时间，则将其选中；
• 最终输出所有选中的活动及数量。

6.3 经典问题的C语言实现与对比分析

为了更直观地理解动态规划与贪心算法的适用场景与性能差异，我们将通过三个经典问题（背包问题、最长公共子序列、活动选择问题）进行实现与对比。

6.3.1 0-1背包问题与完全背包问题的对比

问题类型	是否可重复选	是否适合贪心	是否适合动态规划
0-1背包	否	否	是
完全背包	是	可能	是

完全背包问题的状态转移方程 ：

dp[i][w] = max(dp[i-1][w], dp[i][w - wt[i-1]] + val[i-1])

与0-1背包相比，完全背包允许重复选择当前物品，因此在状态转移时使用 dp[i][w - wt[i-1]] 而非 dp[i-1][w - wt[i-1]] 。

6.3.2 最长公共子序列（LCS）的动态规划实现

最长公共子序列问题（LCS）是典型的动态规划应用场景，其状态转移方程如下：

if (X[i-1] == Y[j-1])
    dp[i][j] = dp[i-1][j-1] + 1;
else
    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);

完整C语言实现如下：

#include <stdio.h>
#include <string.h>

int max(int a, int b) {
    return (a > b) ? a : b;
}

void lcs(char *X, char *Y, int m, int n) {
    int dp[m+1][n+1];

    for (int i = 0; i <= m; i++) {
        for (int j = 0; j <= n; j++) {
            if (i == 0 || j == 0)
                dp[i][j] = 0;
            else if (X[i-1] == Y[j-1])
                dp[i][j] = dp[i-1][j-1] + 1;
            else
                dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
        }
    }

    char lcs[dp[m][n]+1];
    lcs[dp[m][n]] = '\0';

    int i = m, j = n, index = dp[m][n];
    while (i > 0 && j > 0) {
        if (X[i-1] == Y[j-1]) {
            lcs[--index] = X[i-1];
            i--; j--;
        } else if (dp[i-1][j] > dp[i][j-1])
            i--;
        else
            j--;
    }

    printf("LCS: %s\n", lcs);
}

int main() {
    char X[] = "AGGTAB";
    char Y[] = "GXTXAYB";
    int m = strlen(X);
    int n = strlen(Y);
    lcs(X, Y, m, n);
    return 0;
}

流程图说明 ：

graph TD
    A[输入两个字符串] --> B[初始化状态表]
    B --> C[填充状态表]
    C --> D[回溯构造LCS]
    D --> E[输出结果]

6.4 动态规划与贪心算法的优化技巧

在实际应用中，动态规划和贪心算法的性能优化至关重要，尤其是在处理大规模数据时。

6.4.1 空间优化：滚动数组技巧

在动态规划中，如果状态转移只依赖于上一层的数据，可以使用滚动数组来节省空间。例如，在0-1背包问题中，可以将二维状态表优化为一维：

int dp[W+1] = {0};

for (int i = 0; i < n; i++) {
    for (int w = W; w >= wt[i]; w--) {
        dp[w] = max(dp[w], dp[w - wt[i]] + val[i]);
    }
}

这里内层循环必须从后往前遍历，避免覆盖上一轮的结果。

6.4.2 时间优化：剪枝与状态压缩

• 剪枝 ：在递归或状态转移过程中，提前判断某些不可能达到最优解的情况，提前跳过。
• 状态压缩 ：对于某些状态只依赖前几个状态的问题（如斐波那契数列），可以将状态压缩为两个变量。

6.5 实战项目：动态规划与贪心算法的融合应用

在实际项目中，动态规划与贪心算法往往结合使用。例如，在路径规划中，贪心算法用于快速获取一个可行解，动态规划用于优化路径。

6.5.1 项目场景：最小路径和问题

给定一个 m x n 网格，每个格子中的数字表示该位置的代价，从左上角出发，只能向右或向下移动，求到达右下角的最小路径和。

#include <stdio.h>

int minPathSum(int grid[3][3], int m, int n) {
    int dp[3][3];
    dp[0][0] = grid[0][0];

    for (int i = 1; i < m; i++)
        dp[i][0] = dp[i-1][0] + grid[i][0];

    for (int j = 1; j < n; j++)
        dp[0][j] = dp[0][j-1] + grid[0][j];

    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[i][j] = grid[i][j] + (dp[i-1][j] < dp[i][j-1] ? dp[i-1][j] : dp[i][j-1]);
        }
    }

    return dp[m-1][n-1];
}

int main() {
    int grid[3][3] = {
        {1, 3, 1},
        {1, 5, 1},
        {4, 2, 1}
    };

    printf("最小路径和为：%d\n", minPathSum(grid, 3, 3));
    return 0;
}

代码逻辑分析 ：

• 初始化第一行和第一列；
• 对于每个 dp[i][j] ，取上边或左边的最小值，加上当前格子的值；
• 最终返回 dp[m-1][n-1] 即为最小路径和。

6.6 总结与拓展方向

动态规划与贪心算法作为高级算法设计范式，在C语言中有着广泛的应用场景。通过本章的学习，我们掌握了：

• 动态规划的状态定义与转移方程设计；
• 贪心算法的局部最优策略与实现；
• 多个经典问题的C语言实现；
• 空间与时间优化技巧；
• 动态规划与贪心算法在实际项目中的融合应用。

在后续章节中，我们将进一步探讨如何将这些算法模块化、封装为可复用的算法库，并在大型项目中高效调用与测试。

7. C语言项目实战与算法模板参考

在本章中，我们将进入 C 语言编程的实战阶段，探讨如何在真实项目中整合数据结构与算法，构建模块化、可复用的代码结构，并提供经典的算法模板参考。通过本章的学习，读者将掌握在大型项目中如何组织和优化算法模块，如何调试和部署项目，以及如何进行性能评估与优化。

7.1 大型项目中的算法整合

7.1.1 数据结构与算法的模块化设计

在实际项目中，良好的模块化设计是保证代码可维护性和可扩展性的关键。我们可以通过头文件（ .h ）与源文件（ .c ）的分离方式，将数据结构和算法封装成独立模块。

例如，我们设计一个链表模块：

// list.h
#ifndef LIST_H
#define LIST_H

typedef struct Node {
    int data;
    struct Node *next;
} Node;

Node* create_node(int data);
void insert_head(Node** head, int data);
void print_list(Node* head);
void free_list(Node* head);

#endif // LIST_H

对应的实现文件：

// list.c
#include "list.h"
#include <stdio.h>
#include <stdlib.h>

Node* create_node(int data) {
    Node* node = (Node*)malloc(sizeof(Node));
    if (!node) return NULL;
    node->data = data;
    node->next = NULL;
    return node;
}

void insert_head(Node** head, int data) {
    Node* node = create_node(data);
    if (!node) return;
    node->next = *head;
    *head = node;
}

void print_list(Node* head) {
    while (head) {
        printf("%d -> ", head->data);
        head = head->next;
    }
    printf("NULL\n");
}

void free_list(Node* head) {
    Node* temp;
    while (head) {
        temp = head;
        head = head->next;
        free(temp);
    }
}

主程序调用：

// main.c
#include "list.h"

int main() {
    Node* head = NULL;
    insert_head(&head, 10);
    insert_head(&head, 20);
    print_list(head);
    free_list(head);
    return 0;
}

7.1.2 算法库的封装与调用实践

为了提高算法的复用性，可以将常用排序、查找、动态规划等算法封装为静态库或动态库。例如：

将排序算法封装为 sortlib.c ：

// sortlib.c
#include <stdio.h>

void bubble_sort(int arr[], int n) {
    for (int i = 0; i < n - 1; ++i) {
        for (int j = 0; j < n - i - 1; ++j) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

生成静态库：

gcc -c sortlib.c -o sortlib.o
ar rcs libsort.a sortlib.o

主程序链接使用：

gcc main.c -L. -lsort -o main

7.2 经典算法源码解析与优化建议

7.2.1 源码分析方法与调试技巧

在调试 C 程序时，推荐使用 GDB（GNU Debugger）进行逐行调试。例如：

gcc -g main.c -o main
gdb ./main

进入 GDB 后，可以使用以下命令：

命令	功能说明
break main	在 main 函数设置断点
run	运行程序
next	执行下一行代码
print variable	查看变量值
backtrace	查看调用栈

7.2.2 常见性能瓶颈与优化方案

在大型项目中，常见的性能瓶颈包括：

• 内存泄漏（Memory Leak）
• 频繁的内存分配释放
• 低效的循环结构
• 不合理的数据结构选择

优化建议：

1. 使用 valgrind 检测内存泄漏：
   bash valgrind --leak-check=full ./main

2. 减少 malloc/free 次数，使用内存池技术。

3. 将重复计算的表达式提前计算并缓存。
4. 使用更高效的数据结构，如哈希表替代线性查找。

7.3 C语言算法项目的部署与测试

7.3.1 项目编译与链接流程

一个完整的 C 项目通常包含多个模块，使用 Makefile 可以自动化编译流程。例如：

CC = gcc
CFLAGS = -Wall -Wextra -g

OBJS = main.o list.o sortlib.o
TARGET = project

$(TARGET): $(OBJS)
    $(CC) $(CFLAGS) $(OBJS) -o $(TARGET)

main.o: main.c list.h
list.o: list.c list.h
sortlib.o: sortlib.c

clean:
    rm -f $(OBJS) $(TARGET)

执行编译：

make

7.3.2 单元测试与性能评估方法

我们可以使用 assert 进行简单的单元测试，例如：

#include <assert.h>

void test_bubble_sort() {
    int arr[] = {5, 3, 8, 1};
    int expected[] = {1, 3, 5, 8};
    bubble_sort(arr, 4);
    for (int i = 0; i < 4; ++i) {
        assert(arr[i] == expected[i]);
    }
}

运行测试：

gcc -DDEBUG test.c -o test
./test

对于性能评估，可以使用 time 命令：

time ./main

输出示例：

real    0m0.001s
user    0m0.000s
sys     0m0.000s

也可以使用 clock() 函数在程序中测量执行时间：

#include <time.h>

clock_t start = clock();
// 执行算法
clock_t end = clock();
double time_used = ((double)(end - start)) / CLOCKS_PER_SEC;
printf("Time used: %f seconds\n", time_used);

（注：根据要求，本章节未在结尾添加总结性语句。）

本文还有配套的精品资源，点击获取

简介：该资源包含近200个经典C语言源码，专注于算法的设计与实现，是深入学习C语言和算法的宝贵资料。内容涵盖基础语法、指针操作、数据结构、排序查找、递归与动态规划等核心技术，适用于算法爱好者、编程学习者及项目开发人员。通过实际源码分析与练习，学习者可全面提升C语言编程能力与算法思维，为开发高性能系统级应用打下坚实基础。

本文还有配套的精品资源，点击获取