前缀函数和 KMP “跳步骤“模式匹配

在一篇由字符构成的长文中查找另一个短字符串出现的位置，这可以算是编程领域最最常见的问题（比如按下 Ctrl + F 就可以打开你浏览器的查找功能）。这个问题叫做字符串的模式匹配，我们把被查找的关键词叫做模式串，被查找的全文叫做主串。注意：本文的下标均从 0 开始。

当我们用最容易想到的朴素的暴力解法时，就像逐字逐句地翻动书页：将模式串的每个字符与主串逐一比对，一旦发现不匹配，就把模式串右移一位，重新从头比较。

面对随机数据，算法可以高效工作。但这种老实人的做法，在遇到某些“狡猾”的数据时会彻底崩溃。比如：

• 主串：AAAAA……AAB（连续100万个A后跟一个B）
• 模式串：AAAAAAAC

暴力解法会怎么做？它会在主串的每一个位置，逐个对比前7个字符，直到发现第7位的A与C不匹配，再右移一位重复这个过程，最终一共进行了八百万次匹配，最终还是没有找到。

💣 问题的核心：每次匹配失败时，必须全部重来。在主串的每一位匹配时，都可能遍历到模式串的最后一位。这种“一朝失足，从头再来”的策略，在极端情况下让时间复杂度飙升至 $O(mn)$。

前缀函数——模式串的"自省密码"

既然暴力解法卡在「匹配失败就全体重来」的死胡同里，我们需要让模式串学会自我反省——这就是前缀函数（Prefix Function）的使命。它像一本预先生成的密码手册，记录了模式串中每个位置的最长重复头尾特征。

定义与直觉

对于一个长度为 $n$ 的模式串 $s$，前缀函数 $\pi [i]$ 表示子串 $s[\mathrm{0..}i]$ 中，最长的相同真前缀与真后缀的长度。
（真前缀：不包含整个字符串的前缀；真后缀同理）

举个栗子🌰：模式串 "ababcabab"

索引：0 1 2 3 4 5 6 7 8  
字符：a b a b c a b a b  
π[i]:0 0 1 2 0 1 2 3 4  

• i=0 时子串是 "a"，真前缀不应该包括自己（否则每个点的 π 都包含自身全部了） → π[0] 总是 0
• i=3 时子串是 "abab"，最长真前后缀是 "ab" → π[3]=2
• i=8 时子串是整个字符串，真前后缀 "abab" → π[8]=4

为什么能加速？

当我们在主串中匹配到某个位置失败时，前缀函数告诉我们可以保留已匹配部分的最大共同头尾，直接将模式串滑动到该位置继续匹配，跳过中间的重复检查。

动态规划构造前缀表：模式串的自我匹配

我们怎么求解这个有大用的前缀函数呢？构造前缀函数的过程，本质上是在模式串内部用自己匹配自己。这听起来有点玄乎，但核心思想非常巧妙——利用已计算的前缀值指导后续计算，踩着之前的脚印过河。

// string s = "……"
vector<int> next; // π
 
for (int i = 1; i < s.size(); ++i) {  // next[0]总是 0，从next[1]开始计算
    int j = next[i-1];               // 初始化为前一位的前缀值
    while (j > 0 && s[j] != s[i])    // 不匹配时回退
        j = next[j-1];               // 关键跳跃！
    next[i] = (s[j] == s[i]) ? j + 1 : 0; 
}

假设模式串为 "abababc"，我们手动模拟计算过程：

1. 初始化：next[0] = 0（单个字符无真前后缀）
2. i=1（字符 b）：
   • j = next[0] = 0
   • s[0] = 'a' ≠ 'b' → j 保持 0
   • next[1] = 0
3. i=2（字符 a）：
   • j = next[1] = 0
   • s[0] = 'a' == 'a' → j += 1
   • next[2] = 1
4. i=3（字符 b）：
   • j = next[2] = 1 → 检查 s[1] = 'b' == 'b'
   • 匹配成功 → next[3] = 2
5. i=4（字符 a）：
   • j = next[3] = 2 → 检查 s[2] = 'a' == 'a'
   • 匹配成功 → next[4] = 3
6. i=5（字符 b）：
   • j = next[4] = 3 → 检查 s[3] = 'b' == 'b'
   • 匹配成功 → next[5] = 4
7. i=6（字符 c）：
   • j = next[5] = 4 → s[4] = 'a' ≠ 'c'
   • 回退：j = next[3] = 2 → s[2] = 'a' ≠ 'c'
   • 继续回退：j = next[1] = 0 → s[0] = 'a' ≠ 'c'
   • 最终 next[6] = 0

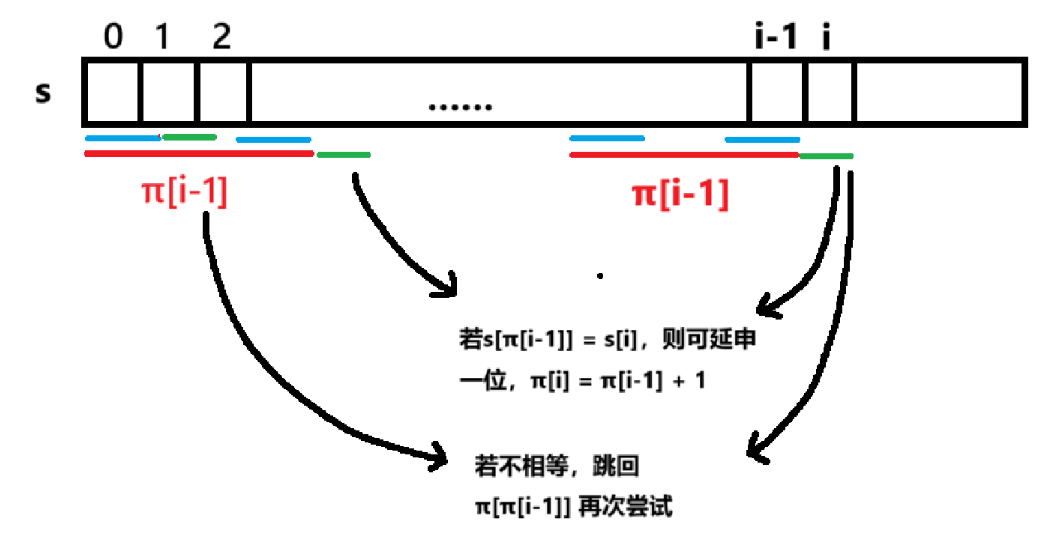
每一次计算next[i]先尝试用next[i-1]，若下一个字符不匹配，无需重头开始，而是可以尝试用next[next[i-1]]来匹配再次尝试，直到其为 0 也不匹配的话，就只能归零了。

j = next[j-1]：当 s[j] ≠ s[i] 时，跳跃到当前最长前缀的末尾继续尝试匹配。这相当于利用之前计算的次长相同前后缀，避免从头开始暴力枚举。

KMP 模式匹配

有了模式串的前缀函数这张“地图”，KMP 算法就能像猎犬追踪气味一样高效搜索。KMP 算法首次出现在1977年，全称为 Knuth-Morris-Pratt 算法，是一种用于在字符串中进行模式匹配的高效算法。它由 Donald Knuth、Vaughan Pratt 和 James H. Morris 三位计算机科学家共同提出，因此命名为 KMP 算法。

它的核心逻辑是让主串指针 i 永不回头，而模式串指针 j 在失败时智能跳跃。

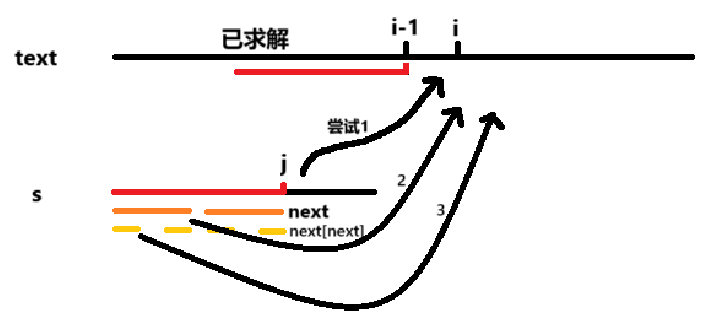
和前缀函数的求解类似，当来到下标 i 时，我们已知主串下标 i-1 的后缀和模式串的前 j 个字符匹配，接下来应该比较s[j] = text[i]，相等则再推进一步，不等则可以退回到和 s[next[j-1]] 比较，直到有一个匹配成功（或者最终仍匹配失败）。

vector<int> match(const string &text) {
    vector<int> result;
    for (int i = 0, j = 0; i < text.size(); ++i) { 
        while (j > 0 && s[j] != text[i]) 
            j = next[j - 1];  
        // 当前字符匹配时，j向前推进
        if (s[j] == text[i]) ++j;
        if (j == s.size()) { // 完整匹配
            result.push_back(i - j + 1); 
            j = next[j - 1]; 
        }
    } 
    return result; 
}

假设：

• 主串 text = "ABABABABC"
• 模式串 s = "ABABAC"（前缀函数 next = [0,0,1,2,3,0]）

1. 初始状态：i=0（指向主串'A'），j=0（指向模式串'A'）

   • 匹配成功 → j=1
   • 未完全匹配 → 继续

2. i=1（主串'B'），j=1（模式串'B'）

   • 匹配成功 → j=2

3. i=2（主串'A'），j=2（模式串'A'）

   • 匹配成功 → j=3

4. i=3（主串'B'），j=3（模式串'B'）

   • 匹配成功 → j=4

5. i=4（主串'A'），j=4（模式串'A'）

   • 匹配成功 → j=5

6. i=5（主串'B'），j=5（模式串'C'）

   • 失配 → 执行 j = next[4] = 3
   • 此时模式串跳跃到 j=3，继续比较 s[3]（'B'）与当前主串字符'B'
   • 匹配成功 → j=4
     …………

稳定的复杂度

初看代码中的 while (j > 0 && s[j] != text[i]) 循环，似乎存在双重循环的风险。但仔细观察，主串指针 i 永远只向前移动，而模式串指针 j 的移动轨迹像弹簧一样——虽然会回缩，但整体趋势必然向前。

1. j 的移动范围：在任何时刻，j 的取值范围是 [0, m]（m为模式串长度）。
2. j 的总增加量：外层循环中，i 从 0 移动到 n（主串长度），每次循环 j 最多增加 1（if (s[j] == text[i]) ++j）。因此，j 在整个算法中最多增加 n 次。
3. j 的回退成本：每次进入 while 循环回退 j 时，j 至少减少 1。由于 j 的总减少量不可能超过总增加量，整个算法的 while 循环最多执行 n 次。

所以 KMP 模式匹配拥有稳定的线性复杂度。

• 构造前缀函数的时间复杂度：O(m)（模式串长度）
• 匹配过程的时间复杂度：O(n)（主串长度）
• 总时间复杂度：O(m + n)，严格线性！

回到最初的灾难性案例：

• 主串：AAAAA...AAB（100万A + B）
• 模式串：AAAAAAAC
• KMP的表现：
  1. 主串指针 i 从 0 移动到 100万，全程无回溯
  2. 每次失配时，模式串指针 j 通过前缀函数迅速回退到 0
  3. 总操作次数 ≈ 100万（主串长度） + 8（模式串长度）

操作	暴力解法	KMP
主串指针移动	反复回退	永不回退
模式串指针移动	每次从头开始	弹性跳跃
极端案例复杂度	O(mn) → 爆炸	O(m+n) → 稳如狗

拓展思考：预装导航地图

仔细观察会发现，KMP的匹配过程本质上是一个状态转移游戏：当前已匹配的字符数 j 构成状态，遇到主串字符 text[i] 时，根据模式串的规律跳转到新状态。

假设我们想用同一个模式串反复匹配不同主串，原始的KMP算法每次匹配时仍需执行 while (j > 0 && s[j] != text[i]) 的跳跃逻辑。其实，若匹配时两次出现“已匹配5个字符，下一个字符是 c”的情况，他们经历的跳转是完全相同的。若我们提前为每个状态 j 和每个可能的字符 c 预计算跳转目标，就能实现查表式一步跳转，将匹配过程优化到极致。

构建一个二维数组 aut[j][c]，表示在状态 j（已匹配前 j 个字符）时，遇到字符 c 应该跳转到哪个新状态。预处理过程如下：

vector<vector<int>> aut(m+1, vector<int>(256)); // m为模式串长度
for (int j = 0; j <= m; ++j) {
    for (char c : 字符集) { // 如ASCII码
        if (j < m && c == s[j]) 
            aut[j][c] = j + 1;  // 直接匹配成功
        else 
            aut[j][c] = aut[next[j]][c]; // 关键递推！
    }
}

这样，我们直接处理出了每一个已匹配长度遇到每一个字符应跳转到哪里，再之后的匹配再也不会出现跳转了，更高效。这种改造将匹配过程中的 while 循环彻底消除，代价是增加了 O(m*|Σ|) 的空间。高频查询时，这是值得的——就像快递员第一次摸清路线后，后续送货直接走最优路径。

以模式串 s = "ABABC" 为例：

• 原始前缀函数 next = [0,0,1,2,0]
• 预处理后，aut[2]['A'] 为3，；因为 AB 后刚好是 A；aut[4]['A'] 也为 3.

方案	预处理时间	单次匹配时间	适用场景
原始KMP	O(m)	O(n)	低频次匹配
自动机优化	O(m*|Σ|)	常数更小的 O(n)	高频次匹配

（其中 |Σ| 为字符集大小，ASCII为256，Unicode需优化存储）

原创作者: ofnoname 转载于: https://www.cnblogs.com/ofnoname/p/18771994