链栈 c语言 源码,[数据结构 - 第4章] 栈之链栈（C语言实现）

一、什么是链栈？

链栈：是指利用链式存储结构实现的栈。

想想看栈只是栈顶来做插入和删除操作，栈顶放在链栈的头部还是尾部呢？由于单链表有头指针，而栈顶指针也是必须的，那干吗不让它俩合二为一呢，所以比较好的办法是把栈顶放在链栈的头部(如下图所示)。另外，都已经有了栈顶在头部了，单链表中比较常用的头结点也就失去了意义，通常对于链栈来说，是不需要头结点的。

对于空栈来说，链表原定义是头指针指向空，那么链栈的空其实就是 top=NULL 的时候。

链栈的结构代码如下:

typedef int ElemType; /* ElemType类型根据实际情况而定，这里假设为int */

/* 链栈结点结构 */

typedef struct StackNode

{

ElemType data;

struct StackNode *next;

}StackNode;

/* 链栈结构 */

typedef struct

{

StackNode *top;

int count;

}LinkStack;

链栈的操作绝大部分都和单链表类似，只是在插入和删除上，特殊一些。

顺序栈与链栈的区别

两者在时间复杂度上是一样的，均为 O(1)。对于空间性能，顺序栈需要事先确定一个固定的长度，可能会存在内存空间浪费的问题，但它的优势是存取时定位很方便，而链栈则要求每个元素都有指针域，这同时也增加了一些内存开销，但对于栈的长度无限制。所以它们的区别和线性表中讨论的一样，如果栈的使用过程中元素变化不可预料，有时很小，有时非常大，那么最好是用链栈，反之，如果它的变化在可控范围内，建议使用顺序栈会更好一些。

二、基本操作

2.1 初始化栈操作

实现代码如下：

// 初始化栈操作

Status initStack(LinkStack **stack)

{

// 注意要给链栈分配内存

*stack = (LinkStack *)malloc(sizeof(LinkStack));

(*stack)->top = NULL; // 链栈的空其实就是 top=NULL 的时候

(*stack)->count = 0;

return TRUE;

}

2.2 进栈操作

对于链栈的进栈 push 操作，假设元素值为 e 的新结点是 s，top 为栈顶指针，示意图如下图所示：

实现代码如下：

// 进栈操作

Status push(LinkStack *stack, ElemType e)

{

StackNode *s = (StackNode *)malloc(sizeof(StackNode));

s->data = e;

s->next = stack->top; // 把当前的栈顶元素赋值给新结点的直接后继，见图中①

stack->top = s; // 将新的结点s赋值给栈顶指针，见图中②

stack->count++;

return TRUE;

}

2.3 出栈操作

至于链栈的出栈 pop 操作，也是很简单的三句操作。假设变量 p 用来存储要删除的栈顶结点，将栈顶指针下移一位，最后释放 p 即可，如下图所示：

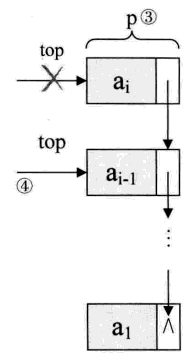
// 出栈操作

Status pop(LinkStack *stack, ElemType *e)

{

StackNode *p;

if (isEmpty(stack))

return FALSE;

*e = stack->top->data;

p = stack->top; // p用来存储要删除的栈顶结点，见图中③

stack->top = stack->top->next; // 使得栈顶指针下移一位，指向后一结点，见图中④

free(p); // 释放结点p

stack->count--;

return TRUE;

}

链栈的进栈 push 和出栈 pop 操作都很简单，没有任何循环操作，时间复杂度均为 O(1)。

2.4 遍历栈操作

实现代码如下：

// 遍历栈操作

Status traverseStack(LinkStack *stack)

{

StackNode *p;

p = stack->top;

while (p)

{

printf("%d ", p->data);

p = p->next;

}

printf("\n");

return TRUE;

}

三、完整程序

#include

#include

#define TRUE 1

#define FALSE 0

#define MAXSIZE 20 /* 存储空间初始分配量 */

typedef int Status;

typedef int ElemType; /* ElemType类型根据实际情况而定，这里假设为int */

/* 链栈结点结构 */

typedef struct StackNode

{

ElemType data;

struct StackNode *next;

}StackNode;

/* 链栈结构 */

typedef struct

{

StackNode *top;

int count;

}LinkStack;

Status initStack(LinkStack **stack); // 初始化栈操作

Status push(LinkStack *stack, const ElemType e); // 进栈操作

Status pop(LinkStack *stack, ElemType *e); // 出栈操作

Status traverseStack(LinkStack *stack); // 遍历栈操作

Status clearStack(LinkStack *stack); // 清空栈操作

Status isEmpty(LinkStack *stack); // 判断是否为空

Status getTop(LinkStack *stack, ElemType *e); // 获得栈顶元素

int getLength(LinkStack *stack); // 获取栈的长度

// 初始化栈操作

Status initStack(LinkStack **stack)

{

// 注意要给链栈分配内存

*stack = (LinkStack *)malloc(sizeof(LinkStack));

(*stack)->top = NULL; // 链栈的空其实就是 top=NULL 的时候

(*stack)->count = 0;

return TRUE;

}

// 进栈操作

Status push(LinkStack *stack, ElemType e)

{

StackNode *s = (StackNode *)malloc(sizeof(StackNode));

s->data = e;

s->next = stack->top; // 把当前的栈顶元素赋值给新结点的直接后继，见图中①

stack->top = s; // 将新的结点s赋值给栈顶指针，见图中②

stack->count++;

return TRUE;

}

// 出栈操作

Status pop(LinkStack *stack, ElemType *e)

{

StackNode *p;

if (isEmpty(stack))

return FALSE;

*e = stack->top->data;

p = stack->top; // p用来存储要删除的栈顶结点，见图中③

stack->top = stack->top->next; // 使得栈顶指针下移一位，指向后一结点，见图中④

free(p); // 释放结点p

stack->count--;

return TRUE;

}

// 遍历栈操作

Status traverseStack(LinkStack *stack)

{

StackNode *p;

p = stack->top;

while (p)

{

printf("%d ", p->data);

p = p->next;

}

printf("\n");

return TRUE;

}

// 清除栈操作

Status clearStack(LinkStack *stack)

{

StackNode *p;

StackNode *q;

p = stack->top;

while (p)

{

q = p;

p = p->next;

free(q);

}

stack->count = 0;

return TRUE;

}

// 判断是否为空栈

Status isEmpty(LinkStack *stack)

{

return stack->count == 0 ? TRUE : FALSE;

}

// 获得栈顶元素

Status getTop(LinkStack *stack, ElemType *e)

{

if (stack->top == NULL)

return FALSE;

else

*e = stack->top->data;

return TRUE;

}

// 获得栈的长度

int getLength(LinkStack *stack)

{

return stack->count;

}

int main()

{

// 初始化栈

LinkStack *stack;

if (initStack(&stack) == TRUE)

printf("初始化链栈成功！\n\n");

// 入栈操作

for (int j = 1; j <= 10; j++)

push(stack, j);

printf("入栈操作(0-10)!\n\n");

// 出栈操作

int e;

pop(stack, &e);

printf("弹出的栈顶元素e=%d\n\n", e);

// 遍历栈

printf("遍历栈，栈中元素依次为：");

traverseStack(stack);

printf("\n");

// 获得栈顶元素

getTop(stack, &e);

printf("栈顶元素 e=%d 栈的长度为%d\n\n", e, getLength(stack));

// 判断是否为空栈

printf("栈空否：%d(1:空 0:否)\n\n", isEmpty(stack));

// 清空栈

clearStack(stack);

printf("清空栈后，栈空否：%d(1:空 0:否)\n\n", isEmpty(stack));

return 0;

}

输出结果如下图所示：

参考：

《大话数据结构 - 第4章》 栈与队列