http://blog.youkuaiyun.com/xiaojidan2011/article/details/11595869
非常清楚
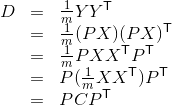
核心部分解释:主成份用于降纬,通过线型变换,从高纬度映射到低纬度,其中映射后结果保持各纬度方差最大化及数据的不相关。p是线性变换的基,y是变换后结果。D是协方差矩阵。变换的目的是得到一组对角协方差矩阵。
根据对称矩阵性质,通过特征值及特征向量得出D的对角线和p。
 本文深入讲解了主成分分析(PCA)的基本原理与应用。通过线性变换将高维数据映射到低维空间中,同时确保各个维度上的方差最大化且数据间不相关。文章详细解释了如何利用协方差矩阵的特征值和特征向量来实现这一目标。
本文深入讲解了主成分分析(PCA)的基本原理与应用。通过线性变换将高维数据映射到低维空间中,同时确保各个维度上的方差最大化且数据间不相关。文章详细解释了如何利用协方差矩阵的特征值和特征向量来实现这一目标。
http://blog.youkuaiyun.com/xiaojidan2011/article/details/11595869
非常清楚
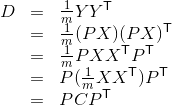
核心部分解释:主成份用于降纬,通过线型变换,从高纬度映射到低纬度,其中映射后结果保持各纬度方差最大化及数据的不相关。p是线性变换的基,y是变换后结果。D是协方差矩阵。变换的目的是得到一组对角协方差矩阵。
根据对称矩阵性质,通过特征值及特征向量得出D的对角线和p。
 1369
1369
 764
764

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


