第3章
常用概率分布
第2章介绍了概率运算的抽象规则。为了使用这些规则,还需要定义若干概率分布。概率分布Pr(x)的选择取决于建模数据x的定义域(见表3-1)。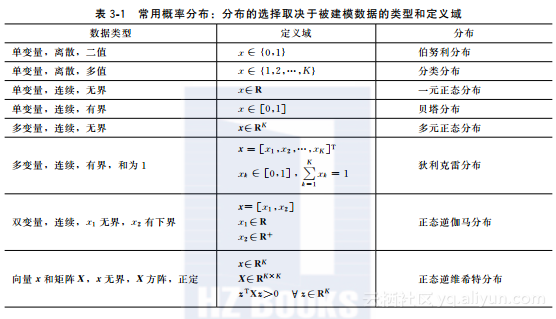
概率分布对视觉数据的建模显然是有用的,例如分类分布和正态分布。然而,其他分布往往并非如此,例如,狄利克雷分布存在总和为1的K个正数,视觉数据通常不采用这种形式。
解释如下:当拟合数据的概率模型时,需要知道拟合的不确定性。该不确定性用拟合模型参数的概率分布来表示。因此对用于建模的每种分布,另有一个与参数联系的概率分布表(见表3-2)。例如,狄利克雷用来建模分类分布的参数。在这种情况下,狄利克雷的参数将称为超参数。一般来说,超参数决定原分布的参数的概率分布的形状。
在详细阐述分布的参数的关系之前,先浏览一下表3-2中的分布。







 本文介绍了概率分布的基础概念及其在数据建模中的应用。通过对比不同的概率分布类型,如正态分布与狄利克雷分布,文章揭示了如何选择合适的概率分布来描述数据,并解释了超参数的作用。
本文介绍了概率分布的基础概念及其在数据建模中的应用。通过对比不同的概率分布类型,如正态分布与狄利克雷分布,文章揭示了如何选择合适的概率分布来描述数据,并解释了超参数的作用。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








