特殊化策略

一、定义

引例，当题目中给定某一个点是圆锥曲线上的任意一点时，满足某种条件，那么这时候如果让这一点成为圆锥曲线的顶点，题目立马就变得简单了许多，这种策略就称为特殊化策略，其本质类似于函数中的赋值法，由此引申，任意角可以取特殊角，任意位置可以取特殊位置，任意形状可以取特殊形状。

二、何时使用

以题目例10为例，我们一般都会画出一个很一般的等腰三角形，但是若将\(\angle A\)变化为\(\cfrac{\pi}{3}\)或\(\cfrac{\pi}{2}\)时，都可以保证不改变题目中给定的已知条件，这时候我们就可以尝试考虑特殊化策略，毕竟图形越特殊，越有利于计算。

三、典例剖析

例1【2016\(\cdot\)山东济南模拟】在\(\Delta ABC\)中，角\(A、B、C\)所对的边分别为\(a、b、c\)，若\(a、b、c\)成等差数列，则\(\cfrac{cosA+cosC}{1+cosAcosC}\)=_______________.

分析：读完题目，我们最容易想到的思路是设三边分别为\(b-d\)，\(b\)，\(b+d\)，然后利用余弦定理分别求解\(cosA\)，\(cosC\)，最后求值。想一想运算的复杂程度，我们都大概能感受到这个解法不太可行。

猜想：当\(a、b、c\)成等差数列时，三个角也是有一定关系的，所求的式子的值应该是定值，那么我们就可以有如下的解法：

法1：【特殊化策略，最特殊】当等差数列的公差为0时，也是满足题意的，此时\(a=b=c\)，则\(A=C=\cfrac{\pi}{3}\)；

故\(\cfrac{cosA+cosC}{1+cosAcosC}=\cfrac{cos\cfrac{\pi}{3}+cos\cfrac{\pi}{3}}{1+cos\cfrac{\pi}{3}cos\cfrac{\pi}{3}}=\cfrac{4}{5}\)；

法2：【特殊化策略，次特殊】我们自然能想到的是\(a=3，b=4，c=5\)的等差数列，(或\(a=6，b=8，c=10\))，则\(cosA=\cfrac{4}{5}\)，\(cosC=0\)，代入原式得到，

\(\cfrac{cosA+cosC}{1+cosAcosC}=\cfrac{\cfrac{4}{5}+0}{1+0}=\cfrac{4}{5}\)。

例2【2019高三理科数学第二次月考第16题】

在平行四边形\(ABCD\)中，点\(M\)在边\(CD\)上，且满足\(DM=\cfrac{1}{3}DC\)，点\(N\)在\(CB\)的延长线上，且满足\(CB=BN\)，若\(AB=3\)，\(AD=4\)，则\(\overrightarrow{AM}\cdot \overrightarrow{NM}\)的值为__________。

分析：我们一般做出的平行四边形是\(\angle BAD\neq 90^{\circ}\)的，从形上思考求向量的内积时几乎没有思路，

此时我们不妨思考，能不能建立直角坐标系，引入点的坐标，然后利用坐标运算内积。这是一个突破；由形到数的思维转化；

其次，观察你做出来的平行四边形，当边\(AD\)绕着点\(A\)逆时针旋转时，我们仍可以保证边\(AB\)和\(AD\)的长度不变化，

那么此时自然就会想起来“特殊化策略”，这是思维上的第二个突破；

【特殊化策略】将平行四边形\(ABCD\)直接特殊化为矩形，以点\(A\)为原点，分别以\(AB、AD\)所在直线为\(x\)轴和\(y\)轴，建立平面直角坐标系，

则点\(A(0，0)\)，点\(M(1，4)\)，点\(N(3，-4)\)，则\(\overrightarrow{AM}=(1，4)\)，\(\overrightarrow{NM}=(-2，8)\)，

则\(\overrightarrow{AM}\cdot \overrightarrow{NM}=(1，4)\cdot (-2，8)=-2+32=30\)。

例3【2018浙江六校联考，选择改编为填空】

已知向量\(\vec{a}\)，\(\vec{b}\)是单位向量，若\(\vec{a}\cdot \vec{b}=0\)，且\(|\vec{c}-\vec{a}|+|\vec{c}-2\vec{b}|=\sqrt{5}\)，则\(|\vec{c}+2\vec{a}|\)的取值范围是_________。

分析：利用向量减法的几何意义确定\(|\vec{c}-\vec{a}|+|\vec{c}-2\vec{b}|=\sqrt{5}\)表达的图形和\(|\vec{c}+2\vec{a}|\)的几何意义。

解法1：由于向量\(\vec{a}\)，\(\vec{b}\)是相互垂直的单位向量，不妨采用特殊化策略，

设\(\vec{a}=(1，0)\)，\(\vec{b}=(0，1)\)，将向量\(\vec{c}\)的起点放置在坐标原点，

则\(|\vec{c}-\vec{a}|+|\vec{c}-2\vec{b}|\)的几何意义就是向量\(\vec{c}\)的终点到向量\(\vec{a}\)，向量\(2\vec{c}\)的终点\((1，0)\)和\((0，2)\)的距离之和，

由于这两点间的距离等于\(\sqrt{5}\)，故向量\(\vec{c}\)的终点在以\((1，0)\)，\((0，2)\)为端点的线段上，

该线段所在的直线方程为\(x+\cfrac{y}{2}=1(0\leq x\leq 1)\)，

\(|\vec{c}+2\vec{a}|=|\vec{c}-(-2\vec{a})|\)的几何意义是向量\(\vec{c}\)的终点到向量\(-2\vec{a}\)的终点\((-2，0)\)的距离，

显然最大距离即为点\((-2，0)\)到点\((1，0)\)的距离\(3\)，最小距离为点\((-2，0)\)到直线\(x+\cfrac{y}{2}=1\)的距离，

此距离为\(d=\cfrac{|-2-1|}{\sqrt{1+\frac{1}{4}}}=\cfrac{6\sqrt{5}}{5}\)；

故\(|\vec{c}+2\vec{a}|\)的取值范围是\([\cfrac{6\sqrt{5}}{5}，3]\)。

例4【2018·广州综合测试】

已知数列\(\{a_n\}\)为等比数列，若\(a_4＋a_6＝10\)，则\(a_7(a_1＋2a_3)＋a_3a_9\)的值为 【】

$A.10$ $B.20$ $C.100$ $D.200$

【法1】分析：\(a_7(a_1＋2a_3)＋a_3a_9=a_7a_1+2a_3a_7+a_3a_9\)

\(=a_4^2+2a_4a_6+a_6^2=(a_4+a_6)^2=10^2=100\)。故选\(C\)。

【法2】：特殊化策略，由于题目数列\(\{a_n\}\)为等比数列，\(a_4＋a_6＝10\)，则可以将其特殊化为\(a_4=a_6=5\)的特殊的等比数列，即常数列，

此时\(a_n=5\)，代入运算得到\(a_7(a_1＋2a_3)＋a_3a_9=100\)，故选\(C\)。

例5【抽象和具体】

已知某数列的前\(2n\)项的和为\((2n)^3\)，且前\(n\)个偶数项的和为\(n^2(4n+3)\)，则它的前\(n\)个奇数项的和为【】

$A.-3n^2(n+1)$ $B.n^2(4n-3)$ $C.-3n^2$ $D.\cfrac{1}{2}n^3$

法1：抽象思考，由题目可知，\(S_{2n}=(2n^3)\)，其中的前\(n\)个偶数项的和，也就是其所有偶数项的和\(S_{偶}=n^2(4n+3)\)，则它的前\(n\)个奇数项的和，也就是所有的奇数项的和\(S_{奇}=S_{2n}-S_{偶}=n^2(4n-3)\)。故选\(B\)。

法2：抽象化为具体，不妨令\(n=1\)，则\(S_{2n}=S_2\)，只有两项\(S_2=a_1+a_2\)，此时就容易理解前\(n\)个偶数项的和为\(n^2(4n+3)\)，即就是\(a_2\)，它的前\(n\)个奇数项的和也就是\(a_1\)，也就能容易理解所求即\((2n)^3-n^2(4n+3)=n^2(4n-3)\)，故选\(B\)。

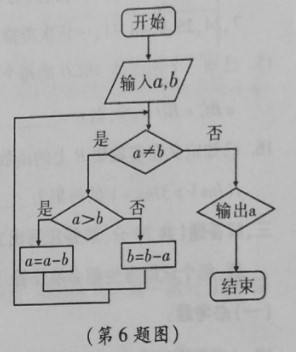
例6【2019届宝鸡市高三理科数学质检Ⅰ第6题】
现执行如图所示的程序框图，该算法的功能是【】

\(A.\)求两个正数\(a\)，\(b\)的最小公倍数

\(B.\)判断两个正数\(a\)，\(b\)是否相等

\(C.\)判断其中一个正数能否被另一个正数整除

\(D.\)求两个正数\(a\)，\(b\)的最大公约数

分析：抽象问题具体化，采用特殊化策略，

令\(a=6\)，\(b=8\)，按程序框图执行，

STEP1：\(a\neq b\)，是，\(a>b\)，否，\(b=2\)；

STEP2：\(a\neq b\)，是，\(a>b\)，是，\(a=4\)；

STEP3：\(a\neq b\)，是，\(a>b\)，是，\(a=2\)；

STEP4：\(a\neq b\)，否，输出\(a=2\)；

即算法的功能是利用“更相减损术”求两个正数的最大公约数。故选\(D\)。

例7【2019届高三理科数学资料用题】【2016北京卷】

袋中装有偶数个球，其中红球和黑球各占一半，甲乙丙为三个空盒子，每次从袋中任意取出两个球，将其中一个球放入甲盒，如果这个球是红球，就将另一个球放入乙盒，否则就放入丙盒，重复上述过程，知道袋中所有球都被放入盒中，则【】

$A.乙盒中黑球不多于丙盒中黑球$ $B.乙盒中红球与丙盒中黑球一样多$

$C.乙盒中红球不多于丙盒中红球$ $D.乙盒中黑球与丙盒中红球一样多$

法1：待录

法2：特殊化策略，设袋中有两个球，红球和黑球各一个，(想一想为什么可以这样？)

现取出两个球，若第一次直接将红球放入甲盒中，则黑球要放入乙盒；全部放置完毕。(想一想为什么可以这样？)

则此时乙盒中红球\(0\)个，黑球\(1\)个；丙盒中红球\(0\)个，黑球\(0\)个；则排除\(A、D\)；

设袋中有四个球，红球和黑球各两个，(想一想为什么可以这样？)

若第一次直接取出的两个球为红球，将红球其一放入甲盒中，则另一个红球放入乙盒；

第二次取出的两个球为黑球，将黑球其一放入甲盒中，则另一个黑球放入丙盒，全部放置完毕。

则此时乙盒中红球\(1\)个，黑球\(0\)个；丙盒中红球\(0\)个，黑球\(1\)个；则排除\(C\)；

故选\(B\)；

例8【2017-18高三理科高考冲刺模拟试题9第15题】
已知由样本数据点集合\(\{(x_i，y_i)\mid i=1，2，\cdots，n\}\)求得的回归直线方程为\(\hat{y}=1.5x+0.5\)，且\(\bar{x}=3\)，现发现两个数据点\((1.1，2.1)\)和\((4.9，7.9)\)误差较大，去除后重新求得的回归直线\(l\)的斜率为\(1.2\)，那么，当\(x=2\)时，\(y\)的估计值是______。

法1：由于样本中心点\((\bar{x}，\bar{y})\)必在回归直线上，先代入计算得到\(\bar{y}=5\)，

即原数据的样本中心点为\((3，5)\)，故\(\sum\limits_{i=1}^{n}x_i=3n\)，\(\sum\limits_{i=1}^{n}y_i=5n\)，

由于\(1.1+4.9=6\)，\(2.1+7.9=10\)，去除两个样本点后，

新的样本中心点的坐标\(\bar{x}=\cfrac{3n-6}{n-2}=3\)，\(\bar{y}=\cfrac{5n-10}{n-2}=5\)，

故新的样本中心点\((3，5)\)必在回归直线\(\hat{y}=1.2x+b\)上，

则有\(5=1.2\times 3+b\)，则\(b=1.4\)，

即重新求得的回归直线\(l\)为\(\hat{y}=1.2x+1.4\)；

当\(x=2\)时，代入计算得到\(\hat{y}=1.2\times 2+1.4=3.8\)。

法2：特殊化策略，将样本数据点的个数认定为\(5\)个，其他的计算仿上完成。

例9【特殊化策略】

设椭圆\(\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1(a>b>0)\)上的动点\(Q\)，过动点\(Q\)做椭圆的切线\(l\)，过右焦点做\(l\)的垂线交\(l\)于点\(P\)，则点\(P\)的轨迹方程为【】

$A.x^2+y^2=a^2$ $B.x^2+y^2=b^2$ $C.x^2+y^2=c^2$ $D.x^2+y^2=e^2$

分析：由于点\(Q\)是椭圆上的任意一个动点，不妨取其在椭圆的四个特殊位置来思考，当点\(Q(a，0)\)时，过动点\(Q\)做椭圆的切线\(l：x=a\)，过右焦点做\(l\)的垂线为\(y=0\)，则点\(P(a，0)\)，代入验证，只有选项\(A\)满足；当点\(Q(0，b)\)时，过动点\(Q\)做椭圆的切线\(l：y=b\)，过右焦点做\(l\)的垂线为\(x=c\)，则点\(P(c，b)\)，代入验证，也只有选项\(A\)满足；故用特殊化策略可知，选\(A\)。

解后反思：如果本题目直接求解，可能会很麻烦，由此也体现出特殊化策略在解选择题时的便捷性。

例10【2019届宝鸡文数质检Ⅲ第10题】在\(\triangle ABC\)中，\(AB=AC=2\sqrt{2}\)，\(\overrightarrow{DB}=3\overrightarrow{AD}\)，连接\(CD\)并取线段\(CD\)的中点为\(F\)，则\(\overrightarrow{AF}\cdot \overrightarrow{CD}\)的值为________。

分析：当\(\triangle ABC\)为等边三角形，或是等腰直角三角形时，题目中的条件仍然不变化，故可以采用特殊化策略，

比如\(\triangle ABC\)为等腰直角三角形，以\(A\)为坐标原点建系，然后利用相应点的坐标计算。\(-\cfrac{15}{4}\)

例11【2019届宝鸡文数质检Ⅲ第10题】已知\(M\)，\(N\)是椭圆\(\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1\) \((a>b>0)\)上关于原点对称的两个点，\(P\)是椭圆上任意一点，直线\(PM\)，\(PN\)的斜率分别是\(k_1\)、\(k_2\)，若\(|k_1k_2|=\cfrac{1}{4}\)，则椭圆的离心率为【】

$A.\cfrac{1}{2}$ $B.\cfrac{\sqrt{2}}{2}$ $C.\cfrac{\sqrt{3}}{2}$ $D.\cfrac{\sqrt{2}}{3}$

分析：采用特殊化策略求解，由于点\(M\)，\(N\)是椭圆\(\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1\) \((a>b>0)\)上关于原点对称的任意的两个点，那么就可以特殊化为椭圆的左右两个顶点，又点\(P\)是椭圆上任意一点，那么就可以特殊化为椭圆上的上顶点，

那么如何让他们满足题目的条件呢，我们可以这样想，只要调整椭圆的三个参数恰当，就可以让其满足题目的条件，这样在这种特殊条件下，

\(k_1=k_{PM}=\cfrac{y_2-y_1}{x_2-x_1}=\cfrac{b-0}{0+a}\)，\(k_2=k_{PN}=\cfrac{b-0}{0-a}\)，

则\(|k_1k_2|=|\cfrac{b^2}{-a^2}|=\cfrac{b^2}{a^2}=\cfrac{1}{4}\)，故\(a^2=4b^2\)，\(c^2=a^2-b^2=3b^2\)，

则\(e^2=\cfrac{c^2}{a^2}=\cfrac{3b^2}{4b^2}=\cfrac{3}{4}\)，故\(e=\cfrac{c}{a}=\cfrac{\sqrt{3}}{2}\)。故选\(C\)。

例12设平行四边形\(ABCD\)中，\(E\)为\(CD\)的中点，\(F\)为\(AE\)的中点，且\(\overrightarrow{BF}=m\overrightarrow{AB}+n\overrightarrow{AD}\)，则\(m+n\)= 【】

$A.\cfrac{1}{4}$ $B.1$ $C.-\cfrac{1}{4}$ $D.-1$

法1：基向量法，选\(C\).

法2：将平行四边形特殊化为矩形，比如长为2，宽为1的矩形，再建系求解，选\(C\).

例17三棱锥\(P-ABC\)中，\(\triangle ABC\)为等边三角形，\(PA=PB=PC=3\)，\(PA\perp PB\)，则三棱锥\(P-ABC\)的外接球的表面积为__________。

分析：补体并特殊化为为正方体的一个角，如图所示，

则体对角线长为\(3\sqrt{3}\)，即\(R=\cfrac{3\sqrt{3}}{2}\)，故\(S_{表}=4\pi R^2=27\pi\).

例13【2019届高三理科数学三轮模拟试题】已知在平面四边形\(MNPQ\)中，\(\overrightarrow{MP}=(2，4)\)，\(\overrightarrow{NQ}=(-4，4)\)，则\(\overrightarrow{MN}\cdot \overrightarrow{PQ}\)的最小值为_________.

分析：特殊化策略，由于平面向量是自由向量，故我们可以将点\(M\)平移到坐标原点，将点\(N\)放置到\(x\)轴上，

故点\(M(0，0)\)，\(N(x，0)\)，则点\(P(2，4)\)，可以计算得到点\(Q(x-4，0)\)，

则\(\overrightarrow{MN}=(x，0)\)，\(\overrightarrow{PQ}=(x-6，-4)\)，

故\(\overrightarrow{MN}\cdot \overrightarrow{PQ}=(x，0)\cdot(x-6，-4)=x(x-6)=(x-3)^2-9\)，

故当\(x=3\)时，其有最小值为\(-9\)。

转载于:https://www.cnblogs.com/wanghai0666/p/8574075.html