堆排序算法与PHP实现

堆排序有点小复杂,分成三块：

第一块,什么是堆,什么是最大堆

第二块,怎么将堆调整为最大堆,这部分是重点

第三块,堆排序介绍

 

第一块,什么是堆,什么是最大堆

什么是堆

这里的堆(二叉堆),指得不是堆栈的那个堆,而是一种数据结构。

堆可以视为一棵完全的二叉树,完全二叉树的一个“优秀”的性质是,除了最底层之外,每一层都是满的,这使得堆可以利用数组来表示,每一个结点对应数组中的一个元素.

数组与堆之间的关系

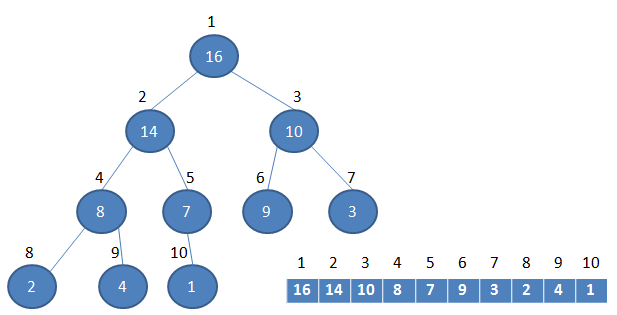
二叉堆一般分为两种：最大堆和最小堆。

什么是最大堆

堆中每个父节点的元素值都大于等于其孩子结点（如果存在）,这样的堆就是一个最大堆

因此,最大堆中的最大元素值出现在根结点(堆顶)

节点与数组索引关系

对于给定的某个结点的下标i，可以很容易的计算出这个结点的父结点、孩子结点的下标，而且计算公式很漂亮很简约

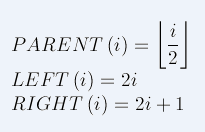
第二块,怎么将堆调整为最大堆,这部分是重点

整个过程如下图所示

在4,14,7这个小堆里边,父节点4小于左孩子14,所以两者交换

在4,2,8这个小堆里边,父节点4小于右孩子8,所以两者交换

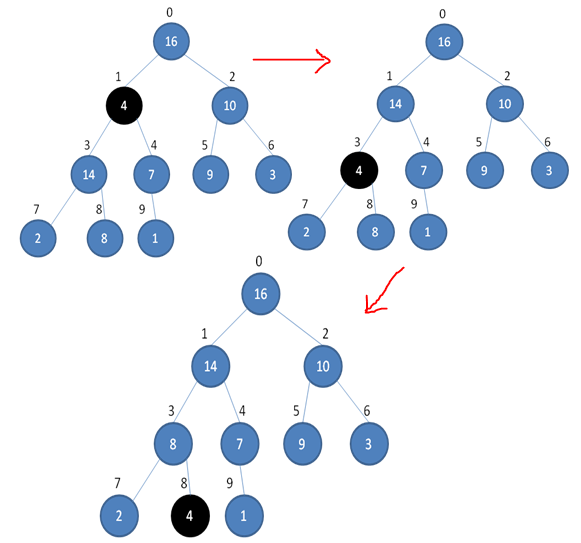
上图展示了一趟调整的过程,这个过程递归实现,直到调整为最大堆为止

第三块,堆排序介绍

堆排序就是把堆顶的最大数取出,

将剩余的堆继续调整为最大堆,具体过程在第二块有介绍,以递归实现

剩余部分调整为最大堆后,再次将堆顶的最大数取出,再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束

下边三张图详细描述了整个过程

 

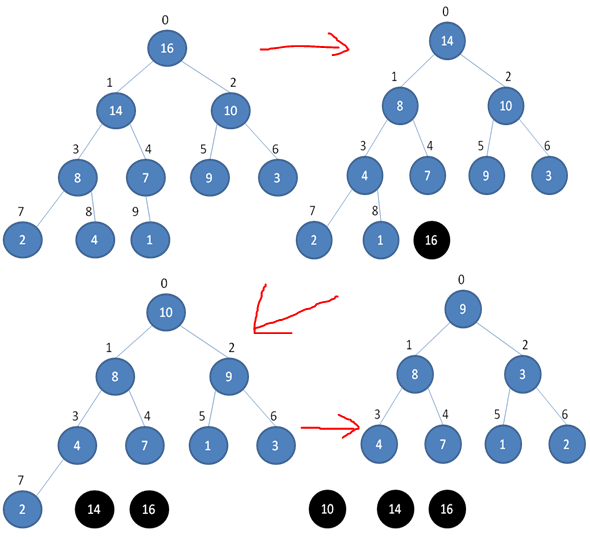
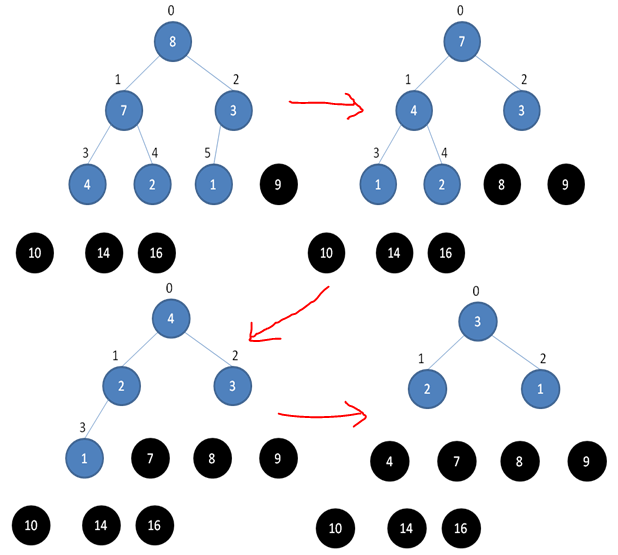
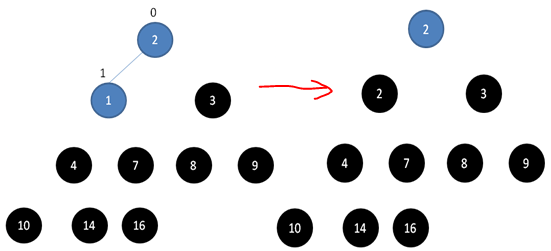
具体PHP实现：

/**
 * 使用异或交换2个值，原理：一个值经过同一个值的2次异或后，原值不变
 * @param int $a
 * @param int $b
 */
function swap(&$a,&$b){
	$a = $a^$b;
	$b = $a^$b;
	$a = $a^$b;
}

/**
 * 整理当前树节点（$n），临界点$last之后为已排序好的元素
 * @param int $n
 * @param int $last
 * @param array $arr
 * 
 */
function adjustNode($n,$last,&$arr){
	$l = $n<<1;	// 左孩子
	if( !isset($arr[$l])||$l>$last ){
		return ;
	}
	$r = $l+1;	// 右孩子
	// 如果右孩子比左孩子大，则让父节点与右孩子比
	if( $r<=$last&&$arr[$r]>$arr[$l] ){
		$l = $r;
	}
	// 如果其中子节点$l比父节点$n大，则与父节点$n交换
	if( $arr[$l]>$arr[$n] ){
		swap($arr[$l],$arr[$n]);
		// 交换之后，父节点($n)的值可能还小于原子节点($l)的子节点的值，所以还需对原子节点($l)的子节点进行调整，用递归实现
		adjustNode($l, $last, $arr);
	}
}

/**
 * 堆排序（最大堆）
 * @param array $arr
 */
function heapSort(&$arr){
	// 最后一个蒜素位
	$last = count($arr);
	// 堆排序中常忽略$arr[0]
	array_unshift($arr, 0);
	// 最后一个非叶子节点
	$i = $last>>1;
	// 整理成最大堆，最大的数放到最顶，并将最大数和堆尾交换，并在之后的计算中，忽略数组最后端的最大数(last)，直到堆顶（last=堆顶）
	while(true){
		adjustNode($i, $last, $arr);
		if( $i>1 ){
			// 移动节点指针，遍历所有节点
			$i--;
		}
		else{
			// 临界点$last=1，即所有排序完成
			if( $last==1 ){
				break;
			}
			swap($arr[$last],$arr[1]);
			$last--;
		}
	}
	// 弹出第一个元素
	array_shift($arr);
}

　　

转载于:https://www.cnblogs.com/iampeter/p/3223487.html