Machine Learning 之Logistic回归算法中最小二乘法的Matlab曲线拟合

Machine Learning 之Logistic回归算法中最小二乘法的Matlab曲线拟合

逻辑回归是机器学习（Machine Learning）中常见的机器学习算法，在处理逻辑回归（Logistic Regression）离散数据点集时，最常用的算法是最小二乘法。古代欧洲没有“平方”的叫法，“二乘”其实就是平方。逻辑回归是相对于线性回归而言，线性回归可以较好拟合连续值。但是现实世界中的数据样本往往是非连续性的。逻辑回归可以构建更理想的拟合曲线，拟合现实世界中的散列数据集。
matlab提供了polyfit和polyval支持最小二乘法。举个例子，以常见的曲线方程：




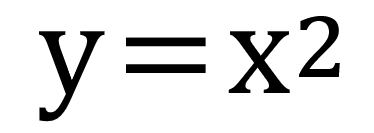
为例。现在给y增加少量的随机噪音，然后生成一些不规则、散列的点，然后算出这些散列点的拟合曲线。matlab代码：

t=randn(1,101);

x=[-10:0.2:10];
y=x.^2+t*6; 
s=scatter(x,y); 
s.LineWidth = 0.6;
s.MarkerEdgeColor = 'g';
s.MarkerFaceColor = [0 0.7 0.7];
hold on; 

p=polyfit(x,y,2)
y1=polyval(p,x);
plot(x,y1,'-r','LineWidth',1);

grid on;

p =

    0.9988   -0.0762    0.9286

拟合曲线（红色）结果如图：

本例是在y=x*x，y值上增加小的常量随机噪音6*t，那么逻辑回归后的多项式，理想结果应该还是y=x*x。经过拟合后的多项式系数为：

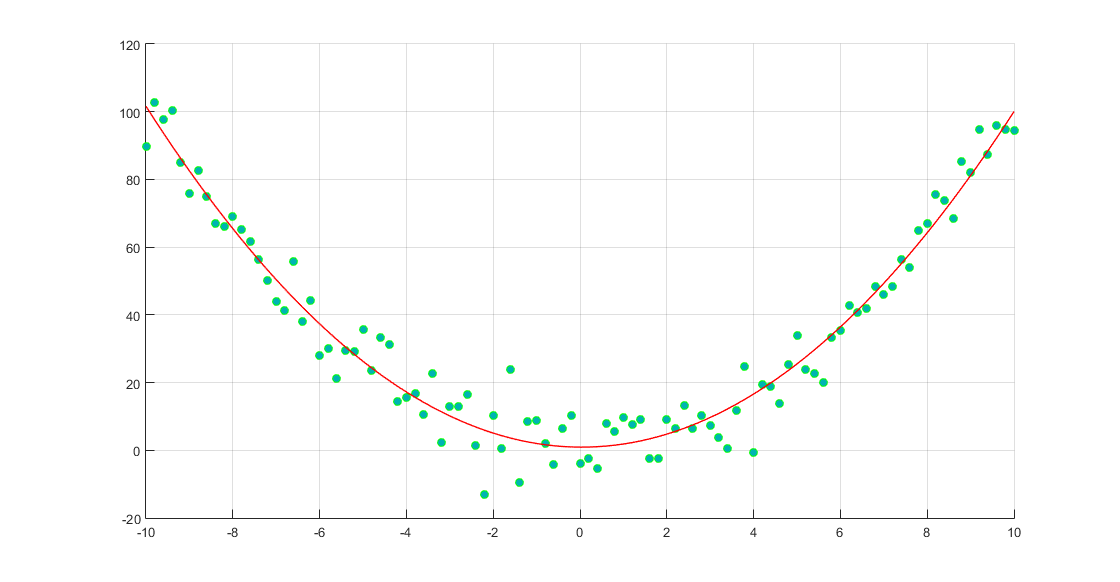
p =

    0.9988   -0.0762    0.9286

最终获得拟合的多项式即为：

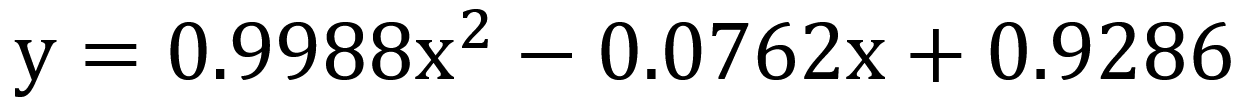
拟合结果很好的拟合了围绕y=x*x的随机散列点。