UVA 10518 How Many Calls?

最新推荐文章于 2020-03-24 15:38:31 发布

weixin_34384915

最新推荐文章于 2020-03-24 15:38:31 发布

阅读量51

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/zufezzt/p/5245161.html

本文介绍了一种使用矩阵乘法解决递推式第n项求模运算问题的方法，通过构造特定矩阵实现快速计算，适用于大规模数据处理场景。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题意：一个递推式第n项%b是多少。

递推式：

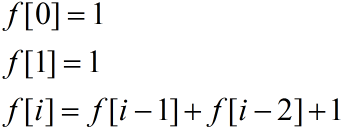
构造矩阵：

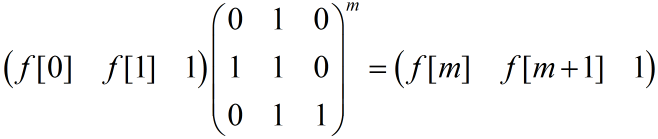
#include<cstdio>
#include<cstring>
#include<cmath>
#include<vector>
#include<algorithm>
using namespace std;

long long MOD;
long long n;

struct Matrix
{
    long long A[20][20];
    int R, C;
    Matrix operator*(Matrix b);
};

Matrix X, Y, Z;

Matrix Matrix::operator*(Matrix b)
{
    Matrix c;
    memset(c.A, 0, sizeof(c.A));
    int i, j, k;
    for (i = 1; i <= R; i++)
    for (j = 1; j <= b.C; j++)
    for (k = 1; k <= C; k++)
        c.A[i][j] = (c.A[i][j] + (A[i][k] * b.A[k][j]) % MOD) % MOD;
    c.R = R; c.C = b.C;
    return c;
}

void init()
{
    memset(X.A, 0, sizeof X.A);
    memset(Y.A, 0, sizeof Y.A);
    memset(Z.A, 0, sizeof Z.A);

    Z.R = 1; Z.C = 3;
    Z.A[1][1] = Z.A[1][2] = Z.A[1][3] = 1;

    X.R = 3; X.C = 3;
    X.A[1][1] = 0; X.A[1][2] = 1; X.A[1][3] = 0;
    X.A[2][1] = 1; X.A[2][2] = 1; X.A[2][3] = 0;
    X.A[3][1] = 0; X.A[3][2] = 1; X.A[3][3] = 1;

    Y.R =3; Y.C = 3;
    for (int i = 1; i <= 3; i++) Y.A[i][i] = 1;
}

void work()
{
    while (n)
    {
        if (n % 2 == 1) Y = Y*X;
        n = n >> 1;
        X = X*X;
    }
    Z = Z*Y;

    printf("%lld\n", Z.A[1][1]);
}

int main()
{
    int Case = 1;
    while (~scanf("%lld%lld", &n, &MOD))
    {
        if (!n&&!MOD) break;
        init();
        printf("Case %d: %lld %lld ", Case++, n, MOD);
        work();
    }
    return 0;
}