洛谷P1962 斐波那契数列

传送门

 

不难得到状态转移矩阵

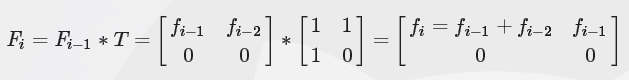
然后带进去乱搞

 1 //minamoto
 2 #include<iostream>
 3 #include<cstdio>
 4 #include<cstring>
 5 #define ll long long
 6 using namespace std;
 7 const int mod=1e9+7;
 8 struct Matrix{
 9     ll g[2][2];
10     Matrix(){memset(g,0,sizeof(g));}
11     Matrix(int Arr[2][2]){
12         for(int i=0;i<2;++i) for(int j=0;j<2;++j)
13         g[i][j]=Arr[i][j];
14     }
15     inline Matrix operator *(Matrix b){
16         Matrix ans;
17         for(int i=0;i<2;++i)
18         for(int j=0;j<2;++j)
19         for(int k=0;k<2;++k)
20         (ans.g[i][j]+=g[i][k]*b.g[k][j])%=mod;
21         return ans;
22     }
23 };
24 ll n;
25 int main(){
26     scanf("%lld",&n);if(n<=2) return puts("1"),0;
27     n-=2;
28     int a[2][2]={{1,1},{0,0}};
29     int b[2][2]={{1,1},{1,0}};
30     Matrix A(a),B(b);
31     while(n){
32         if(n&1) A=A*B;
33         B=B*B,n>>=1;
34     }
35     printf("%lld\n",A.g[0][0]);
36     return 0;
37 }

 

转载于:https://www.cnblogs.com/bztMinamoto/p/9593759.html