总结---2-优快云博客

1.各种排序算法的时间复杂度和空间复杂度分析

选择排序、快速排序、希尔排序、堆排序不是稳定的排序算法，
冒泡排序、插入排序、归并排序和基数排序是稳定的排序算法。

排序法	平均时间	最差情形	稳定度	额外空间	备注
冒泡	O(n²)	O(n²)	稳定	O(1)	n小时较好
交换	O(n²)	O(n²)	不稳定	O(1)	n小时较好
选择	O(n²)	O(n²)	不稳定	O(1)	n小时较好
插入	O(n²)	O(n²)	稳定	O(1)	大部分已排序时较好
基数	O(log_RB)	O(log_RB)	稳定	O(n)	B是真数(0-9)， R是基数(个十百)
Shell	O(nlogn)	O(n^s) 1<s<2	不稳定	O(1)	s是所选分组
快速	O(nlogn)	O(n²)	不稳定	O(nlogn)	n大时较好
归并	O(nlogn)	O(nlogn)	稳定	O(1)	n大时较好
堆	O(nlogn)	O(nlogn)	不稳定	O(1)	n大时较好

名称	复杂度	说明	备注
冒泡排序 BubbleSort	O(N*N)	将待排序的元素看作是竖着排列的 “ 气泡 ” ，较小的元素比较轻，从而要往上浮
插入排序 InsertionSort	O(N*N)	逐一取出元素，在已经排序的元素序列中从后向前扫描，放到适当的位置	起初，已经排序的元素序列为空
选择排序 SelcetionSort	O(N*N)	首先在未排序序列中找到最小元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小元素，然后放到排序序列末尾。以此递归。
快速排序 QuickSort	O(n*log₂ (n))	先选择中间值，然后把比它小的放在左边，大的放在右边（具体的实现是从两边找，找到一对后交换）。然后对两边分别使用这个过程（递归）。
堆排序 HeapSort	O(n*log₂ (n))	利用堆（ heaps ）这种数据结构来构造的一种排序算法。堆是一个近似完全二叉树结构，并同时满足堆属性：即子节点的键值或索引总是小于（或者大于）它的父节点。	近似完全二叉树
希尔排序 ShellSort	O(n¹⁺ ^￡) 0<￡ <1	选择一个步长 (Step) , 然后按间隔为步长的单元进行排序 . 递归 , 步长逐渐变小 , 直至为 1.
箱排序 BinSort	O(n)	设置若干个箱子，把关键字等于 k 的记录全都装入到第 k 个箱子里 ( 分配 ) ，然后按序号依次将各非空的箱子首尾连接起来 ( 收集 ) 。	分配排序的一种：通过 " 分配 " 和 " 收集 " 过程来实现排序。
桶排序 BucketSort	O(n)	桶排序的思想是把 [0 ， 1) 划分为 n 个大小相同的子区间，每一子区间是一个桶。	分配排序的一种：通过 " 分配 " 和 " 收集 " 过程来实现排序。

详细分析见：http://www.cnblogs.com/heyonggang/p/3356930.html

2.满二叉树

在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。

满二叉树的特点有：

叶子只能出现在最下一层。出现在其他层就不可能达到平衡。
非叶子结点的度一定是2 。否则就是“缺胳膊少腿”了。
在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多。

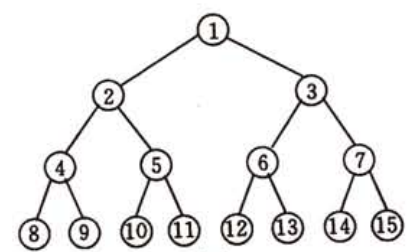
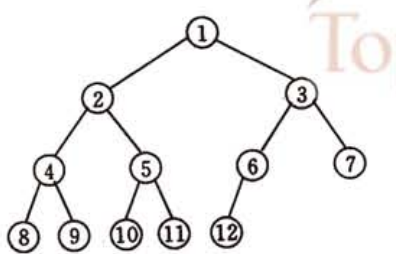
3.完全二叉树

对一棵具有n个结点的二叉树按层序编号，如果编号为i（1≤i≤n）的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。

顺序存储结构一般只使用于完全二叉树。

完全二叉树的特点：

叶子结点只能出现在最下两层。
最下层的叶子一定集中在右部连续位置。
倒数第二层，若有叶子结点，一定都在右部连续位置。
如果结点度为1，则该结点只有左孩子，即不存在只有右子树的情况。
同样结点数的二叉树，完全二叉树的深度最小。

从这些特点可以得出一个判断是否是完全二叉树的方法：那就是看着树的示意图，心中默念给每个结点按照满二叉树的结构逐层顺序编号，如果编号出现空档，就说明不是完全二叉树，否则就是。

4.二叉树性质

性质1：在二叉树的第i层上至多有2^i-1个结点。

性质2：深度为k的二叉树至多有2^k- 1个结点（k≥1）。

性质3：对任何一棵二叉树T，如果其终端结点数为n₀，度为2的结点数为n₂，则n₀=n₂+1 。

性质4：具有n个结点的完全二叉树的深度[log₂n+1] ([x]表示不大于x的最大整数)。

性质5：如果对一棵有n个结点的完全二叉树（其深度为[log₂n]+1）的结点按层序编号（从第1层到第[log₂n]+1层，每层从左到右），对任一结点i（1≤i≤n）有：

如果i=1，则结点i是二叉树的根，无双亲；如果i>1，则其双亲是结点[i/2]。
如果2i>n，则结点i无左孩子（结点i为叶子结点）；否则其左孩子是结点2i。
如果2i+1>n，则结点i无右孩子；否则其右孩子是结点2i+1 。

5.____的先序序列和后序序列正好相反。

A.二叉排序树 B.3个结点的二叉树 C.平衡二叉树 D.无右孩子的二叉树

本文转自夏雪冬日博客园博客，原文链接：http://www.cnblogs.com/heyonggang/p/3356935.html，如需转载请自行联系原作者

总结---2

选择排序、快速排序、希尔排序、堆排序不是稳定的排序算法，

冒泡排序、插入排序、归并排序和基数排序是稳定的排序算法。