1531. Zones on a plane
Time Limit: 1.0 second
Memory Limit: 64 MB
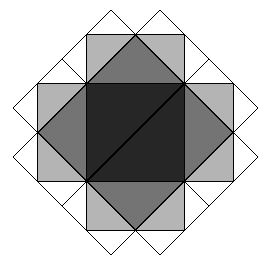
Consider zones
zi on a plane which consist of triangles. Zone
z
1 consists of two right-angled isosceles triangles, forming a square. Zone
z
n + 1 is produced from zone
zn in the following way. For each triangle from the previous zone, construct two isosceles right-angled triangles on each of its two legs as a hypotenuse. Then, remove every triangle that is a part of a zone with lower number. The remaining triangles constitute the zone
z
n + 1.
Given an integer number
n, find how many simple polygons constitute the zone
zn.
Input
There is a single integer
n (1 ≤
n ≤ 2000) on the first line of the input.
Output
Output a single number — the number of simple polygons zone
zn consists of.
Samples
| input | output |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 8 |
| 4 | 12 |
Problem Source: Dmitry Gozman Contest 1, Petrozavodsk training camp, January 2007
解答如下:
1
using
System;
2
3 namespace Skyiv.Ben.Timus
4 {
5 // http://acm.timus.ru/problem.aspx?space=1 &num=1531
6 sealed class T1531
7 {
8 static void Main()
9 {
10 Console.WriteLine(Zones( int .Parse(Console.ReadLine())));
11 }
12
13 static BigInteger Zones( int n)
14 {
15 if (n == 1 ) return 1 ;
16 if (n == 2 ) return 4 ;
17 BigInteger z = 4 , c = 2 ;
18 for ( int i = 3 ; i <= n; i ++ , z += c) if (i % 2 != 0 ) c *= 2 ;
19 return z;
20 }
21 }
22 }
2
3 namespace Skyiv.Ben.Timus
4 {
5 // http://acm.timus.ru/problem.aspx?space=1 &num=1531
6 sealed class T1531
7 {
8 static void Main()
9 {
10 Console.WriteLine(Zones( int .Parse(Console.ReadLine())));
11 }
12
13 static BigInteger Zones( int n)
14 {
15 if (n == 1 ) return 1 ;
16 if (n == 2 ) return 4 ;
17 BigInteger z = 4 , c = 2 ;
18 for ( int i = 3 ; i <= n; i ++ , z += c) if (i % 2 != 0 ) c *= 2 ;
19 return z;
20 }
21 }
22 }
注意,这个程序使用了 BigInteger 类,请到我的另一篇随笔 Timus 1013. K-based numbers. Version 3 中查看其源代码。
这道题目是说,在平原上有若干三角形组成的区域 Zi。Z1 包含两个等腰直角三角形,组成一个正方形。Zn+1 由 Zn 按以下方法生成:以 Zn 中的三角形的直角边作为新的等腰直角三角形的斜边,然后再移去 Zn 中的三角形,剩下的三角形就组成了 Zn+1。现在要求计算 Zn 中包含多少个简单多边形。
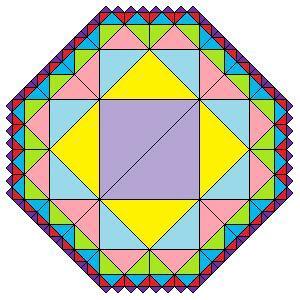
为了找出其中的规律,我们继续画图,一直画到 n = 8,如右图所示。然后在右图中数出 Zn 来,如下:
1, 4, 8, 12, 20, 28, 44, 60
我们发现,该数列后项减前项为:
3, 4, 4, 8, 8, 16, 16
除了第一个数 3 以外,其余各数依次为:
22, 22, 23, 23, 24, 24
这样,我们就得到以下递推公式 ( [x] 表示对 x 进行下取整 ):
Z1 = 1, Z2 = 4, Zn = Zn-1 + 2[(n+1)/2] (n > 2)
有了递推公式,写出相应的程序就非常容易了。由于 Z2000 ≈ 4.286 x 10301,所以程序中使用 BigInteger 类进行计算。




 本文介绍Timus1531.Zonesonaplane问题,通过构造几何图形序列,求解特定步骤后形成的简单多边形数量。给出了解题思路和递推公式,并提供了一个使用BigInteger类的C#实现。
本文介绍Timus1531.Zonesonaplane问题,通过构造几何图形序列,求解特定步骤后形成的简单多边形数量。给出了解题思路和递推公式,并提供了一个使用BigInteger类的C#实现。

















 22
22

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








