BZOJ 2306 幸福路径（DP）-优快云博客

本文探讨了在一个有向图中寻找从起始点出发，通过特定路径获得最大幸福度的问题。幸福度由点权值与能量值的乘积决定，能量值随路径递减。算法采用动态规划方法，考虑链、环及链加环三种路径情况，最终求得最大期望幸福度。

题目链接：http://61.187.179.132/JudgeOnline/problem.php?id=2306

题意：给出一个有向图，点有权值 a。初始时在点S。一个人在初始点能量为K=1，每走到下一个点能量值乘以p(p<1)，到达一个点u 幸福度为 a[u]*K。求最大的幸福度。

思路：最后必然是走了一条链，或者是一个环（一直绕），或者是一条链加一个环。设f[i][j][k]表示从点j走了i步到达节点k的最大幸福度。那么f[i][j][j]就表示在绕环。那么在这个环上一直绕下去的期望为：

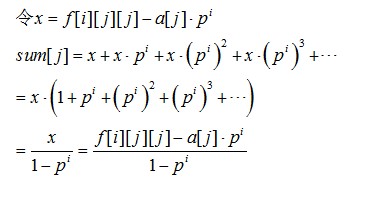
那么从S走i步到j再在j开始的环上绕圈的期望为：

int n,m,S;
double f[N][N][N],g[N],Pow[N*10],p;
int u[N*10],v[N*10];
double a[N];


int main()
{
    RD(n,m);
    int i,j,k;
    FOR1(i,n) RD(a[i]);
    RD(S); RD(p);
    Pow[0]=1;
    FOR1(i,N-1) Pow[i]=Pow[i-1]*p;
    FOR1(i,m) RD(u[i],v[i]);
    FOR0(i,n+1) FOR0(j,n+1) FOR0(k,n+1) f[i][j][k]=-dinf;
    FOR1(i,n) g[i]=f[0][i][i]=a[i];
    FOR1(i,n) FOR1(j,n) FOR1(k,m)
    {
        upMax(f[i][j][v[k]],f[i-1][j][u[k]]+a[v[k]]*Pow[i]);
    }
    FOR1(i,n) for(j=i;j<=n;j++) 
    {
        upMax(g[i],(f[j][i][i]-a[i]*Pow[j])/(1-Pow[j]));
    }
    double ans=0;
    FOR1(i,n) FOR1(j,n) upMax(ans,f[j][S][i]-a[i]*Pow[j]+Pow[j]*g[i]);
    PR(ans);
}