对OpenCV中3种乘法操作的理解掌握

参考了《Opencv中Mat矩阵相乘——点乘、dot、mul运算详解 》“http://blog.youkuaiyun.com/dcrmg/article/details/52404580”的相关内容。

乘法是线性代数的基本操作，在OpenCV中有三种方法实现了乘法。

一、向量乘法

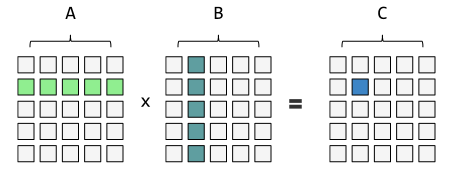
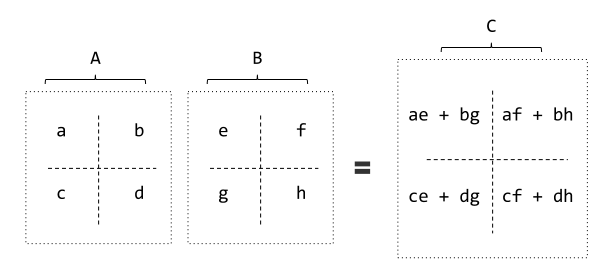
这两幅图像说明的就是向量乘法。在OpenCV中采用" . "来实现，要求是第一个矩阵的列值等于第二个矩阵的行值。且每个矩阵都是float结构。

    Mat A  = Mat( 3, 3,CV_32FC1,Scalar( 0));
    Vec3f v ( 1, 2, 3);
    Mat B  = Mat(v);
     
    A.at < float >( 0, 0) = 1;  
    A.at < float >( 0, 1) = 2;  
    A.at < float >( 0, 2) = 3;  
    A.at < float >( 1, 0) = 4;  
    A.at < float >( 1, 1) = 5;  
    A.at < float >( 1, 2) = 6;  
    A.at < float >( 1, 0) = 4;  
    A.at < float >( 1, 1) = 5;  
    A.at < float >( 1, 2) = 6;
    Mat AB  = A *B;

二、数量乘法

对于输入的矩阵

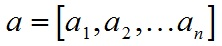
和

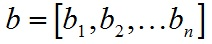
数量乘法的结果为

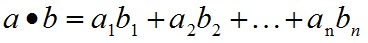
那么可以看出来，这里要求a和b的向量结构是一样的，在OpenCV中，如果a和b是多维向量的话，那么首先是将其拉长为一维向量，然后做乘法。

 

    Mat A =Mat : :ones( 2, 3,CV_8UC1);  
    Mat B =Mat : :ones( 2, 3,CV_8UC1);  
    A.at <uchar >( 0, 0) = 1;  
    A.at <uchar >( 0, 1) = 2;  
    A.at <uchar >( 0, 2) = 3;  
    A.at <uchar >( 1, 0) = 4;  
    A.at <uchar >( 1, 1) = 5;  
    A.at <uchar >( 1, 2) = 6;  
  
    B.at <uchar >( 0, 0) = 1;  
    B.at <uchar >( 0, 1) = 2;  
    B.at <uchar >( 0, 2) = 3;  
    B.at <uchar >( 1, 0) = 4;  
    B.at <uchar >( 1, 1) = 5;  
    B.at <uchar >( 1, 2) = 6;  
    double AB =A.dot(B);  

三、乘法

最后介绍.mul这种乘法。这种乘法就是直接理解意义上的乘法。对于

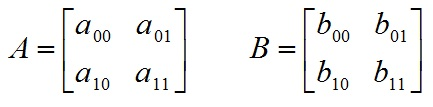
乘法的结果为

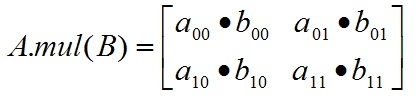
参考代码

 

    Mat A  = Mat( 3, 3,CV_32FC1,Scalar( 0));
    Mat B  = Mat(v);
    A.at < float >( 0, 0) = 1;  
    A.at < float >( 0, 1) = 2;  
    A.at < float >( 0, 2) = 3;  
    A.at < float >( 1, 0) = 4;  
    A.at < float >( 1, 1) = 5;  
    A.at < float >( 1, 2) = 6;  
    A.at < float >( 1, 0) = 4;  
    A.at < float >( 1, 1) = 5;  
    A.at < float >( 1, 2) = 6;
    Mat AB  = A *B;
     //
    Mat C  = Mat( 3, 3,CV_32FC1,Scalar( 0));
    C  = A.clone();
    Mat AC  = A.mul(C);

 

 

 

四、小结

1、以上三种函数，都是以Mat作为输入参数和输出结果的；

2、. 这种乘法要求两个矩阵都是float结果，后两者只要求两个矩阵的结果是一样的；

3、可以看到，.这种乘法要求第一个矩阵的行值等于第二个矩阵的列值，而后两种乘法则要求参加运算的两个矩阵结构完全一样。

 

来自为知笔记(Wiz)