本文提供了多项编程竞赛题目的详细解答，包括二分查找、贪心算法、前缀和及博弈论的应用。针对不同难度的问题，文章给出了清晰的思路解析与高效实现代码。
前言：这次的比赛，除了A题较难一点，学弟们多注意注意细节至少能做三四题的，废话不多说看吧：
(有问题讨论区：)
B.Minion Chef and Bananas
做法：二分
题意：在你面前有n堆香蕉，每次只能吃其中一堆的K个，如果这一堆小于K个那就吃完这一堆，要在H小时内吃完，这个K最大可以为多少。
思路：签到题，只要直接二分这个K就可以了
代码：
#include <bits/stdc++.h> #define INF 0x3f3f3f3f #define FOR(i,a,n) for(register int i=a; i<=n; ++i) #define FDR(i,a,n) for(register int i=a; i>=n; --i) #define mem(a) memset(a, 0, sizeof(a)) typedef long long ll; typedef unsigned long long ull; using namespace std; const int maxn = 100005; const int MOD = 1000000009; int a[maxn]; int n, h; bool check(int m) { ll sum = 0; FOR(i,1,n){sum += a[i]/m;if(a[i]%m != 0)sum++;} return sum <= h ; } int main() { ios::sync_with_stdio(false); int t; cin >> t; while(t--) { cin >> n >> h; FOR(i,1,n)cin >> a[i]; int l = 1, r = INF; while(l < r) { int mid = (l+r)>>1; if(check(mid))r = mid; else l = mid+1; } cout << l << endl; } return 0; }
C.Let us construct palindrome
做法：思维，贪心
题意：给你一个字符串，问你能否通过删除一个字符，使其变成一个回文串。
思路：我们如果考虑暴力的做法每删除一个再暴力判断的话时间复杂度是O(n2)，显然会超时，我们应该换一种思路，假设它原本就是一个回文串，再插入一个字符的话会有什么性质，假设一个回文串abccba，插入了一个字符abcc(o)ba，我们发现是不是它的后面一截还是回文的，所以我们从前往后判断如果遇到不是回文的部分就从当前部分加一，或者后面对应部分减一开始判断是不是回文串，如果其中一个满足就这个字符串是通过插入一个字符得到的，如果它本身就是回文串，它就必然满足。
代码：
#include <bits/stdc++.h> #define INF 0x3f3f3f3f #define FOR(i,a,n) for(register int i=a; i<=n; ++i) #define FDR(i,a,n) for(register int i=a; i>=n; --i) #define mem(a) memset(a, 0, sizeof(a)) #define pb push_back() typedef long long ll; typedef unsigned long long ull; using namespace std; const int maxn = 300005; const int MOD = 1000000009; char str[maxn]; bool check(int l, int r) { while(l < r) { if(str[l] != str[r])return false; else l++, r--; } return true; } int main() { ios::sync_with_stdio(false); int t; cin >> t; while(t--) { cin >> str; int len = strlen(str); int l = 0, r = len-1; bool change = false; bool flag = true; while(l <= r) { if(str[l] == str[r]) { l++, r--; } else { if(check(l+1, r))flag = true; else if(check(l, r-1))flag = true; else flag = false; break; } } if(flag)puts("YES"); else puts("NO"); } return 0; }
F.Count Good Prefixes
做法：前缀和
思路：我们可以把假设a为1，b为-1，设sum[i]为前i个的前缀和，如果sum[i]为正数是不是表示a的数量大于b，如果sum[i]的值为非正数的话是不是表示a的数量小于等于b的数量，首先把第一个循环节的前缀和先算出来，想象一下如果当前的sum[n]为正数的话，说明a的数量大于b，那么是不是这一节的贡献是不是可以使后面的sum[i]变成正数，如果相等的话，是不是对后面的毫无影响，如果为负数的话是不是可以是原本为正数的sum[i]变成负数，所以我们只需计算出sum[n]即可预知后面的变化，具体怎么影响的看代码吧。
代码：
#include <bits/stdc++.h> #define INF 0x3f3f3f3f #define FOR(i,a,n) for(register int i=a; i<=n; ++i) #define FDR(i,a,n) for(register int i=a; i>=n; --i) #define mem(a) memset(a, 0, sizeof(a)) #define pb push_back() typedef long long ll; typedef unsigned long long ull; using namespace std; const int maxn = 100005; const int MOD = 1000000009; char str[maxn]; ll sum[maxn]; int main() { ios::sync_with_stdio(false); ll t, n; cin >> t; while(t--) { cin >> str+1 >> n; int len = strlen(str+1); mem(sum); for(int i = 1; i <= len; i++) { if(str[i] == 'a')sum[i] = sum[i-1]+1; else sum[i] = sum[i-1]-1; } ll add = sum[len]; ll ans = 0; if(add > 0) { for(int i = 1; i <= len; i++) { if(sum[i] > 0)ans += n; else if(n+sum[i]/add-1 > 0)ans += n+sum[i]/add-1; } } else if(add == 0) { for(int i = 1; i <= len; i++) if(sum[i] > 0)ans += n; } else { for(int i = 1; i <= len; i++) { // cout << sum[i] << ' '; if(sum[i] > 0) { if((sum[i]-1)/-add+1 < n)ans += (sum[i]-1)/-add+1; else ans += n; // cout << (sum[i]-1)/add+1 << endl; } } } cout << ans << endl; } return 0; }
D.Game on Stick
做法：博弈论
思路：我们可以明确的一点是这就是一个抢占中点的游戏，谁要是抢到了中间位置就可以直接断线，然后是不是就可以占领一大半的地盘，就是看y1坐标和y2坐标与中点的距离。设d1为先手到中心的距离，d2为后手到中心的距离，然后分情况讨论。如果x1 == x2是不是看谁先到达中心位置谁就赢，但是y1是先手，如果n%2 == 1是不是y1可以占领一半刚好多一个的位置，还有一种情况就是当y1和y2不是同一边，并且n%2 == 0 && 自己到中心的距离和对手到中心的距离刚好小一的时候，是可以和对手打平的。当x1 != x2的时候当d1<d2 && y1与中心的距离和y2与中心的距离之差刚好为一且在同一边时，你是无法占领一半多的位置的，所以是平局，如果d1 == d2显然是平局，当d1 > d2时就留给读者去考虑了（偷个懒~）
代码：
#include <bits/stdc++.h> #define INF 0x3f3f3f3f #define FOR(i,a,n) for(register int i=a; i<=n; ++i) #define FDR(i,a,n) for(register int i=a; i>=n; --i) #define mem(a) memset(a, 0, sizeof(a)) #define pb push_back() typedef long long ll; typedef unsigned long long ull; using namespace std; const int maxn = 100005; const int MOD = 1000000009; int main() { ios::sync_with_stdio(false); int t; cin >> t; while(t--) { ll n, x1, y1, x2, y2; cin >> n >> x1 >> y1 >> x2 >> y2; ll d1, d2; if(n%2 == 0){ if(y1 > n/2)d1 = y1-n/2-1; else d1 = n/2-y1; if(y2 > n/2)d2 = y2-n/2-1; else d2 = n/2-y2; } else { d1 = abs(y1-(n+1)/2); d2 = abs(y2-(n+1)/2); } if(x1 == x2){ if(d1 > d2) { // cout << d1 << ' ' << d2 << endl; if(n%2 == 0 && d1-1 == d2 && !((y1 <= (n+1)/2 && y2 <= (n+1)/2) || (y1 > (n+1)/2 && y2 > (n+1)/2)))cout << "Draw" << endl; else cout << "Slava" << endl; } else if(d1 < d2)cout << "Miron" << endl; else { if(n%2 == 1)cout << "Miron" << endl; else cout << "Draw" << endl; } } else { if(d1 < d2){ if(n%2 == 0 && d1 == d2-1 && !((y1 <= (n+1)/2 && y2 <= (n+1)/2) || (y1 > (n+1)/2 && y2 > (n+1)/2))){ cout << "Draw" << endl; } else cout << "Miron" << endl; } else if(d1 == d2)cout << "Draw" << endl; else { if((y1 <= (n+1)/2 && y2 <= (n+1)/2) || (y1 > (n+1)/2 && y2 > (n+1)/2)){ if(d1-1 > d2)cout << "Slava" << endl; else cout << "Draw" << endl; } else { if(n%2 == 1) { if(d1-1 > d2)cout << "Slava" << endl; else cout << "Draw" << endl; } else { if(d1-2 > d2)cout << "Slava" << endl; else cout << "Draw" << endl; } } } } } return 0; }
E.Cleaning Tables
做法：贪心
思路：这个一看就知道是贪心，关键是如何正确的选取贪心策略，首先我们把桌子座满，考虑桌子中所有编号离自己下一个且相同的编号最远的地方，举个例子假如样例为n = 2, m = 10, 下面的编号为3 2 4 2 3 2 4 1 4 2，首先把3，2坐满，然后来了一个4，我们要从2，3中踢走一个，我们应该踢哪一个呢？按照上述的贪心策略，我们考虑在此之后的2，3；2下一次出现的的位置为下表4，3的下一个出现的位置在下标5，我应该踢掉远的那一个3，所以现在的变成了2，4，然后重复上述过程。特别的当走到了下表编号为5时，当前桌子上是2，3，2的下一个出现位置是下标6，而3就没在出现过了，所以我们应该把3踢掉。
代码：
#include <bits/stdc++.h> #define INF 0x3f3f3f3f #define FOR(i,a,n) for(register int i=a; i<=n; ++i) #define FDR(i,a,n) for(register int i=a; i>=n; --i) #define mem(a) memset(a, 0, sizeof(a)) #define pb push_back() typedef long long ll; typedef unsigned long long ull; using namespace std; const int maxn = 100005; const int MOD = 1000000009; int a[maxn]; int idx[maxn]; int q[maxn]; int main() { ios::sync_with_stdio(false); int t; cin >> t; while(t--) { int n, m; cin >> n >> m; memset(idx, 0, sizeof(idx)); memset(a, 0, sizeof(a)); for(int i = 1; i <= m; i++)cin >> a[i]; int tot = 0; int ans = 0; for(int i = 1; i <= m; i++) { if(tot < n){ if(idx[a[i]])continue; ++tot; idx[a[i]] = tot; q[tot] = a[i]; ans++; } else { if(idx[a[i]])continue; int sign = 0; int vis[500]; memset(vis, INF, sizeof(vis)); for(int j = i; j <= m; j++) { if(idx[a[j]] && vis[idx[a[j]]] == INF){ vis[idx[a[j]]] = j; } } int maxs = 0; for(int i = 1; i <= n; i++) { if(maxs < vis[i]){ maxs = vis[i]; sign = i; } } idx[a[i]] = sign; idx[q[sign]] = 0; q[sign] = a[i]; //// cout << a[i] << ' ' << a[idx[sign]] << endl; ans++; } } cout << ans << endl; } return 0; }
A.Count Substrings
做法：前缀和+二分
思路：如果想不到最好的解法那就暴力是试一下吧，首先考虑暴力的做法，在一个区间中l到r的循环，设pre[i]表示如果当选择第i个字符所能到达的最远的距离，然后把所有的这些距离加起来就是答案。
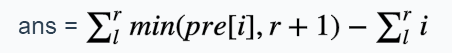
如下：
void init() { int zero = 0, one = 0; int j = 0; for(int i = 1; i <= n; i++) { while(zero <= k && one <= k) { j++; if(j > n)break; if(str[j] == '0')zero++; else one++; } pre[i] = j; if(str[i] == '0')zero--; else one--; } } int main() { ios::sync_with_stdio(false); int t; cin >> t; while(t--) { cin >> n >> k >> q; cin >> str+1; init(); while(q--) { ll ans = 0; ll l, r; cin >> l >> r; for(int i = l; i <= r; i++) { ans += min(pre[i], r+1)-i; } cout << ans << endl; } } return 0; }
但是这样子做的时间复杂度为O(Q*N)明显会超时。我们可以考虑优化，我们发现是不是满足这样的条件pre[i] < pre[j]if(i < j)也就是说之后的pre[j]一定会大于之前的pre[i]，所以我们只需要找到最右边的那个pre[k]，在把i到k的加起来就可以了，至于如何找到，就使用我们学过的二分即可解决问题。
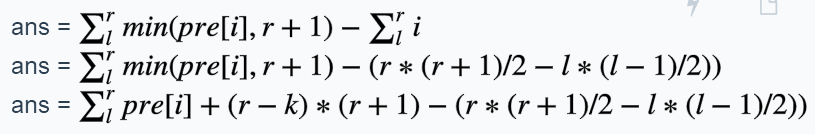
代码：
#include <bits/stdc++.h> #define INF 0x3f3f3f3f #define FOR(i,a,n) for(register int i=a; i<=n; ++i) #define FDR(i,a,n) for(register int i=a; i>=n; --i) #define mem(a) memset(a, 0, sizeof(a)) #define pb push_back() typedef long long ll; typedef unsigned long long ull; using namespace std; const int maxn = 100005; const int MOD = 1000000009; ll n, k, q; int pre[maxn]; ll sumpre[maxn]; char str[maxn]; void init() { int zero = 0, one = 0; int j = 0; for(int i = 1; i <= n; i++) { while(zero <= k && one <= k) { j++; if(j > n)break; if(str[j] == '0')zero++; else one++; } pre[i] = j; if(str[i] == '0')zero--; else one--; } for(int i = 1; i <= n; i++) { sumpre[i] = sumpre[i-1]+pre[i]; } } int main() { ios::sync_with_stdio(false); int t; cin >> t; while(t--) { cin >> n >> k >> q; cin >> str+1; init(); ll ans = 0; while(q--) { ll l, r; cin >> l >> r; ll dl = l-1, dr = r+1; while(dr-dl > 1) { ll mid = (dl+dr)>>1; if(pre[mid] <= r)dl = mid; else dr = mid; } ans = sumpre[dl]-sumpre[l-1]+(r-dl)*(r+1)-(r*(r+1)/2-l*(l-1)/2); cout << ans << endl; } } return 0; }
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
