Machine Learning Techniques -6-Support Vector Regression

最新推荐文章于 2025-09-11 18:44:42 发布

weixin_34357436

最新推荐文章于 2025-09-11 18:44:42 发布

阅读量103

点赞数

CC 4.0 BY-SA版权

文章标签：数据结构与算法

原文链接：http://www.cnblogs.com/windniu/p/4762749.html

本文深入探讨了使用内核函数在平方误差回归中的内核岭回归方法，通过分析βn的形成过程，揭示了大量数据如何影响βn的计算效率，并与软边界Gaussian SVM进行比较，提出了一种通过引入缓冲区和最大函数来优化计算的策略，最终实现了从原始问题到拉格朗日乘子形式的转换，旨在提高计算效率并减少计算资源的消耗。

6-Support Vector Regression

For the regression with squared error, we discuss the kernel ridge regression.

With the knowledge of kernel function, could we find an analytic solution for kernel ridge regression?

Since we want to find the best βn

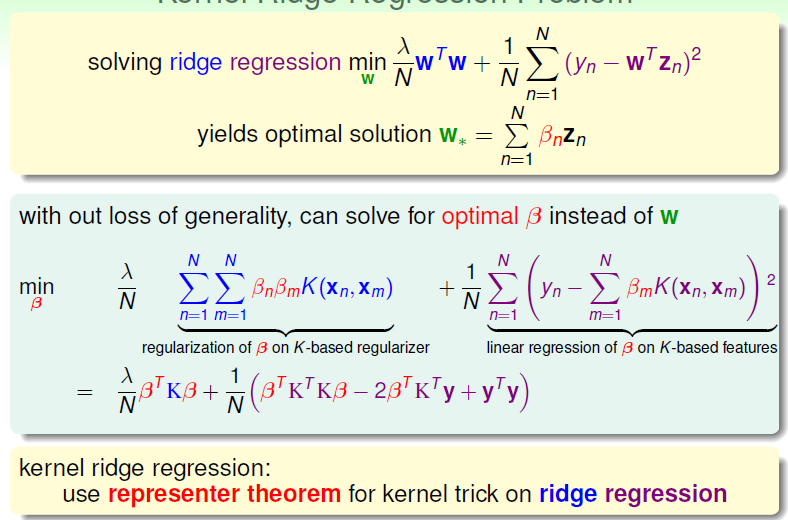
However, compare to the linear situation, the large number of data will suffer from this formation of βn.

Compared to soft-margin Gaussian SVM, kernel ridge regression suffers from the operation of βn through N:

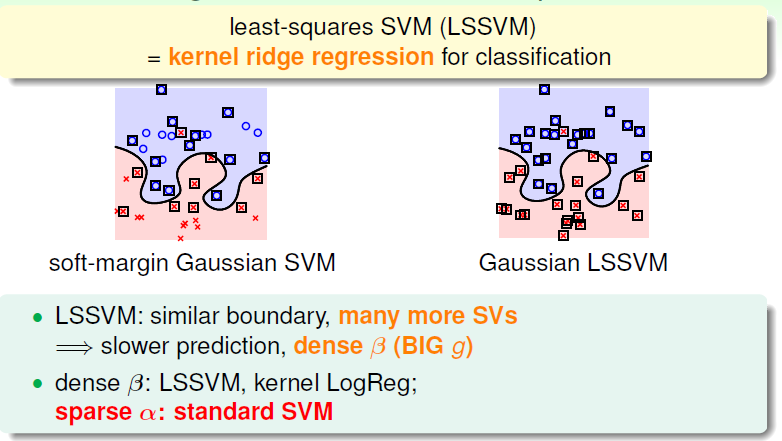
That means more SVs and will slow down our calculation, a sparse βn is now we want.

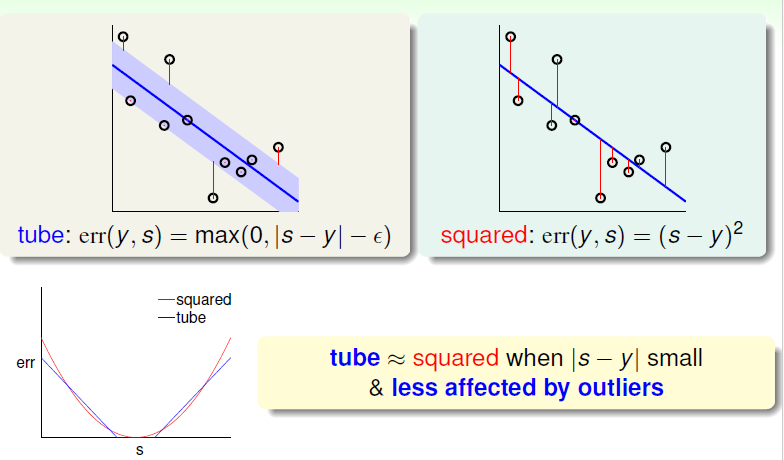
Thus we add a tube, with the familiar function of MAX, we prune the points at a small |s - y|.

Max function is not differentable at some points, so we need some other operation as well.

These operations are about changing the appearance to be more like standard SVM, in order to deal with the tool of QP.

wTZn + b = wTZn +w0, which is separated as a Constant.

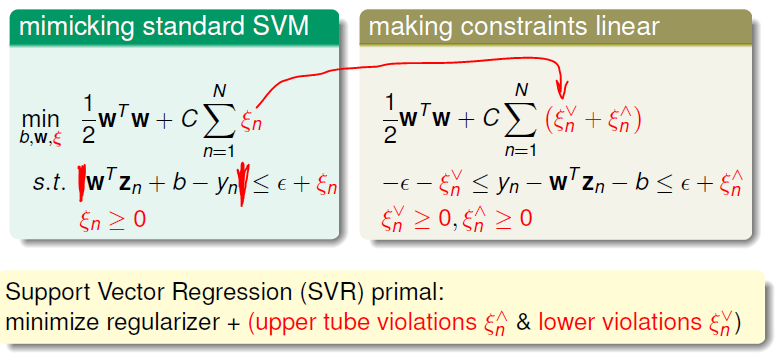
we add a factor to descrip the violation of margin, and use upper and lower bound to keep linear formation.

Our next task : SVR primal -> dual

As usual, we get two common constrain from the gredient to w and b, the dual formation is as followed:

It can also be proved that we could get a sparsity of beta in the tube we defined:

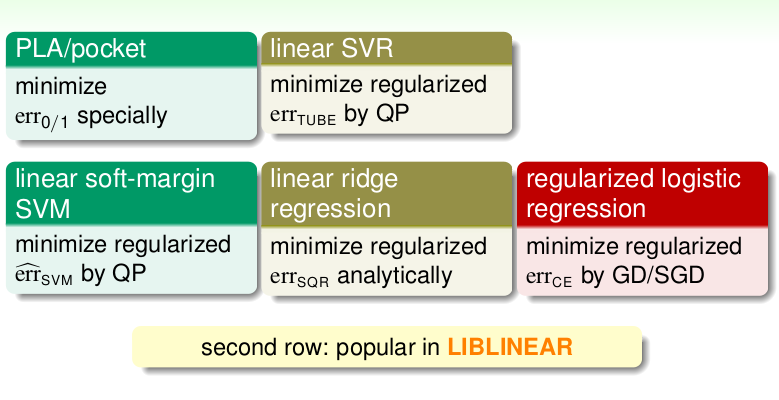
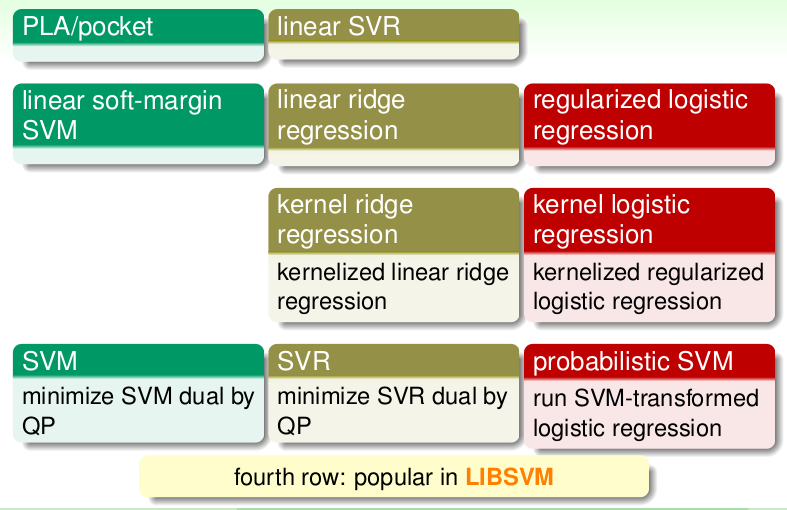
If we compare these methods togather:

转载于:https://www.cnblogs.com/windniu/p/4762749.html